
4-1刚体的定轴转动 刚体的平动与转动 > 刚体:在外力作用下,形状和大小都不发生变化 的物体.(任意两质点间距离保持不变的特殊质点组) 刚体的运动形式:平动、转动. > 平动:若刚体中所有点 的运动轨迹都保持完全相同 或者说刚体内任意两点间的 连线总是平行于它们的初始 位置间的连线。 刚体平动>质点运动
5 –4 1–简谐运动 1 刚体的定轴转动 简谐运动的振幅 周期 频率和相位 ➢ 刚体:在外力作用下,形状和大小都不发生变化 的物体.(任意两质点间距离保持不变的特殊质点组) 刚体的运动形式:平动、转动. 刚体平动 质点运动 ➢ 平动:若刚体中所有点 的运动轨迹都保持完全相同, 或者说刚体内任意两点间的 连线总是平行于它们的初始 位置间的连线. 一 刚体的平动与转动

4-1刚体的定轴转动 > 转动:刚体中所有的点都绕同一直线做圆周运动 转动又分定轴转动和非定轴转动. 刚体的平面运动
5 –4 1–简谐运动 1 刚体的定轴转动 简谐运动的振幅 周期 频率和相位 ➢ 转动:刚体中所有的点都绕同一直线做圆周运动 . 转动又分定轴转动和非定轴转动 . ➢ 刚体的平面运动

4-1刚体的定轴转动 > 刚体的一般运动:质心的平动十绕质心的转动
5 –4 1–简谐运动 1 刚体的定轴转动 简谐运动的振幅 周期 频率和相位 ➢ 刚体的一般运动: 质心的平动 + 绕质心的转动
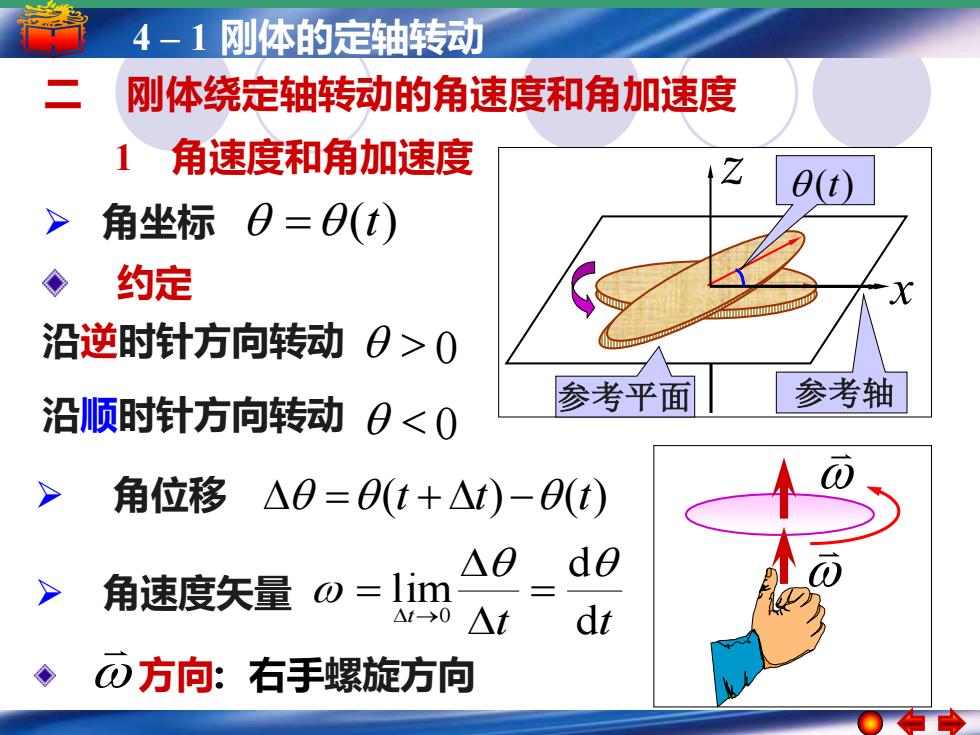
4-1刚体的定轴转动 刚体绕定轴转动的角速度和角加速度 1角速度和角加速度 0(t) > 角坐标0=0(t) ◆ 约定 沿逆时针方向转动0>0 沿顺时针方向转动0<0 参考平面 参考轴 角位移△0=0(t+△t)-O(t) △0 dθ 角速度矢量o=lim △t>0 △t dt ō方向:右手螺旋方向
5 –4 1–简谐运动 1 刚体的定轴转动 简谐运动的振幅 周期 频率和相位 z x 二 刚体绕定轴转动的角速度和角加速度 参考平面 ➢ 角位移 =(t + t) −(t) ➢ 角坐标 = (t) < 0 > 0 约定 沿逆时针方向转动 沿顺时针方向转动 t t t d d lim 0 = = → ➢ 角速度矢量 方向: 右手螺旋方向 参考轴 1 角速度和角加速度 (t)
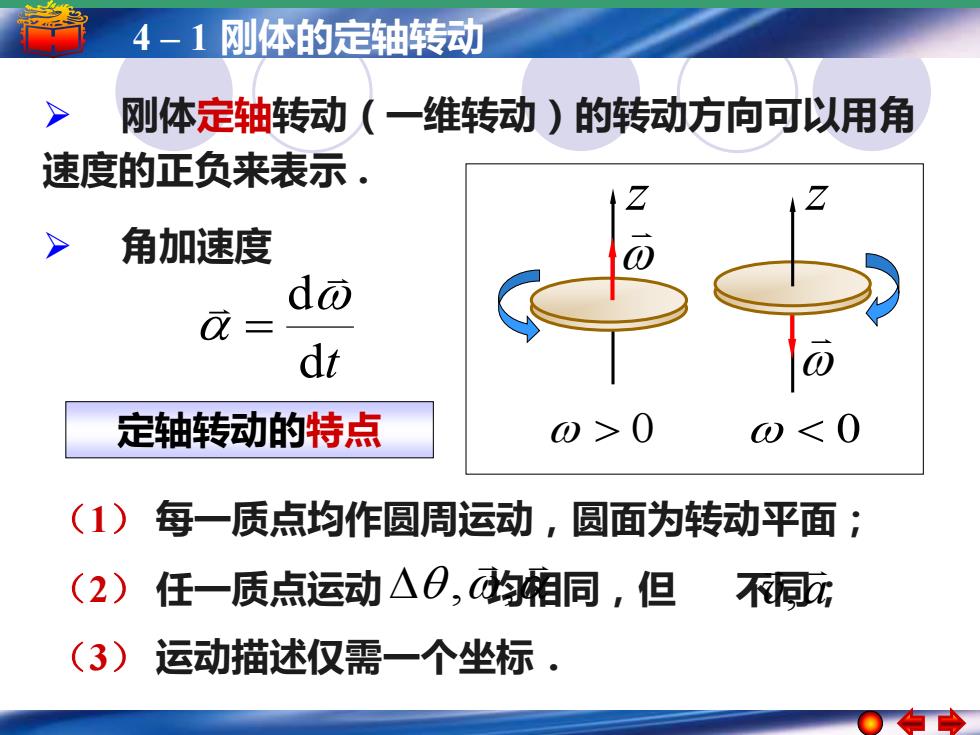
4-1刚体的定轴转动 > 刚体定轴转动(一维转动)的转动方向可以用角 速度的正负来表示 角加速度 do dt 定轴转动的特点 0> <0 (1)每一质点均作圆周运动,圆面为转动平面 (2) 任一质点运动△0,均相同,但 不同玩 (3) 运动描述仅需一个坐标
5 –4 1–简谐运动 1 刚体的定轴转动 简谐运动的振幅 周期 频率和相位 ➢ 角加速度 dt d = (1) 每一质点均作圆周运动,圆面为转动平面; (2) 任一质点运动 均相同,但 不同; (3) 运动描述仅需一个坐标 . , , a v, 定轴转动的特点 ➢ 刚体定轴转动(一维转动)的转动方向可以用角 速度的正负来表示 . > 0 < 0 z z