
3-1质点和质点系的动量定理 F 对时间的累积→p,1 力的累积效应 对空间的累积→W,E 冲量质点的动量定理 ◆动量 p =m) dp d(m) Fdt dp =d(mv) dt dt ∫Fdt=p.-p=,-mo, ◆冲量 力对时间的积分(矢量)了-Fd
5 3 ––11简谐运动 质点和质点系的动量定理 简谐运动的振幅 周期 频率和相位 2 1 2 1 2 1 d v v F t p p m m t t = − = − 一 冲量 质点的动量定理 动量 v p = m t m t p F d d( d d v) = = d d d ( v) F t = p = m 力的累积效应 F W E F p I , , → → 对时间的累积 对空间的累积 冲量 力对时间的积分(矢量) = 2 1 d t t I F t

3-1质点和质点系的动量定理 CFdt=p2-p,=m元2-m而 动量定理在给定的时间内,外力作用在质点上的 冲量,等于质点在此时间内动量的增量. 问:冲量是矢量,它的方向就是力的方向吗? ◆分量形式 (Is=Fdt=m2s -mow I=1i+1,j+Ik I=F,dt=mozy-my F.dt=moz:-mon
5 3 ––11简谐运动 质点和质点系的动量定理 简谐运动的振幅 周期 频率和相位 动量定理 在给定的时间内,外力作用在质点上的 冲量,等于质点在此时间内动量的增量 . 2 1 2 1 2 1 d v v F t p p m m t t = − = − I I i I j I k x y z = + + 分量形式 z z t t z z y y t t y y x x t t x x I F t m m I F t m m I F t m m 2 1 2 1 2 1 2 1 2 1 2 1 d d d v v v v v v = = − = = − = = − 问:冲量是矢量,它的方向就是力的方向吗 ?
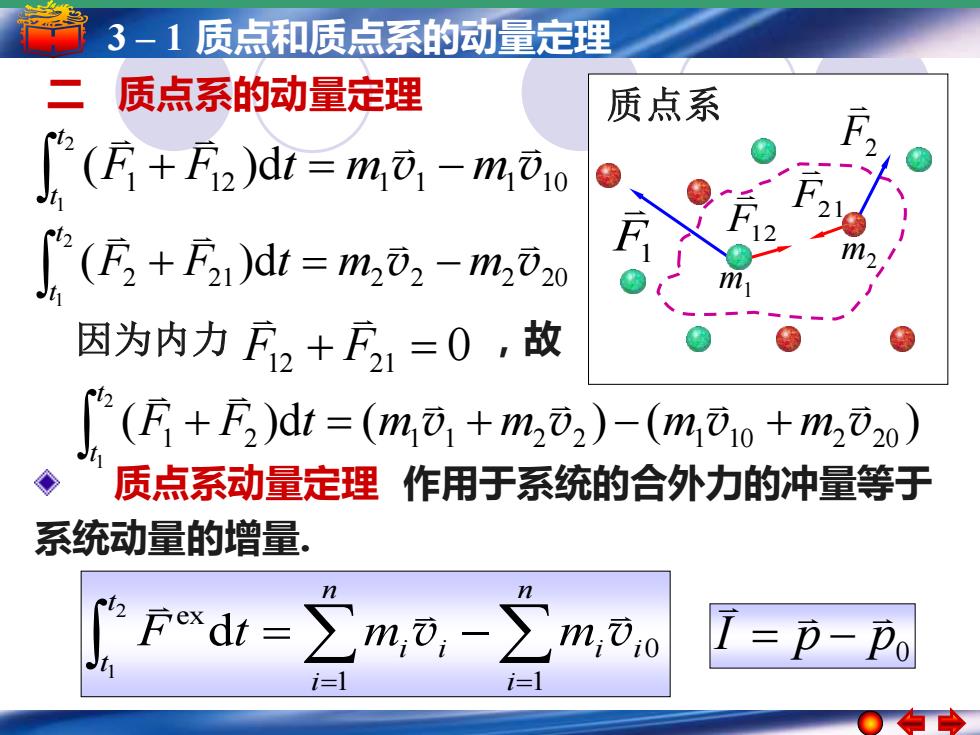
3-1质点和质点系的动量定理 二 质点系的动量定理 质点系 (f+Ea)d=ma-ma。 (E+E1)dt=m,⑦2-m,⑦0 因为内力2+月=0,故 [(R+F)dt=(m⑦,+m,02)-(0m,⑦o+m,0o) 质点系动量定理作用于系统的合外力的冲量等于 系统动量的增量, Fd=ma,-之m,ao I=p-Po i=l
5 3 ––11简谐运动 质点和质点系的动量定理 简谐运动的振幅 周期 频率和相位 二 质点系的动量定理 质点系 m1 m2 F12 F21 F1 F2 质点系动量定理 作用于系统的合外力的冲量等于 系统动量的增量. = = = − n i i i i n i i t t F t m m 1 0 1 ex 2 1 d v v ( )d ( ) ( ) 1 2 1 1 2 2 1 10 2 20 2 1 v v v v F F t m m m m t t + = + − + 2 21 d 2 2 2 20 ( ) 2 1 v v F F t m m t t + = − 1 12 d 1 1 1 10 ( ) 2 1 v v F F t m m t t + = − 因为内力 0 ,故 F12 + F21 = p p0 I = −
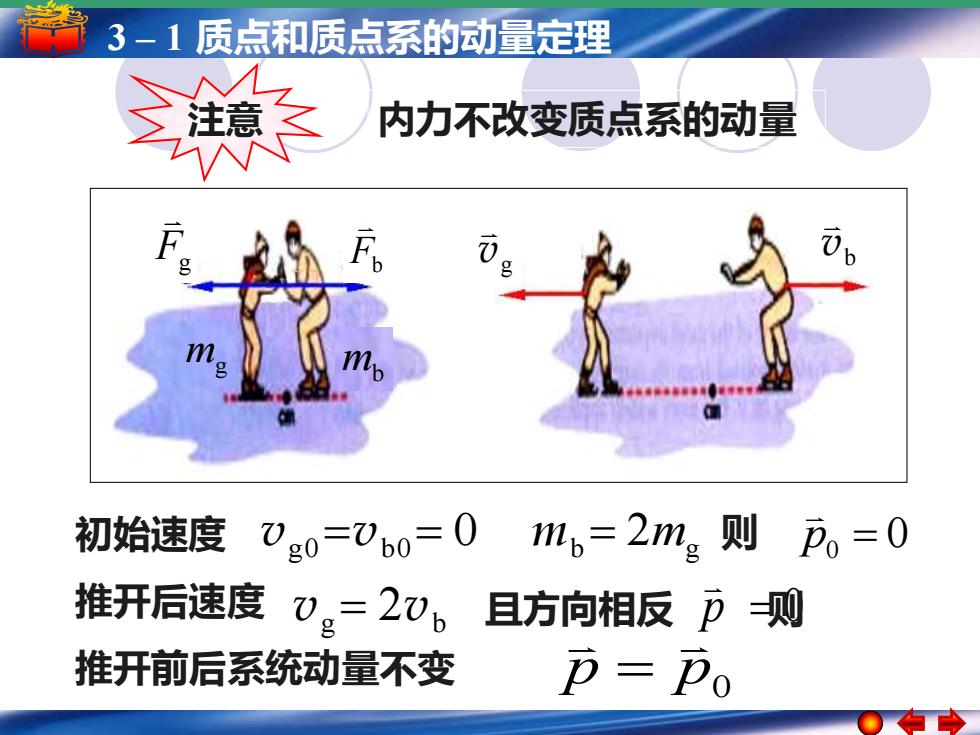
3-1质点和质点系的动量定理 越 内力不改变质点系的动量 初始速度)g0=Vb0=0 b=2m。则p。=0 推开后速度 vg=20b F 且方向相反刀则 推开前后系统动量不变 p=Po
5 3 ––11简谐运动 质点和质点系的动量定理 简谐运动的振幅 周期 频率和相位 注意 内力不改变质点系的动量 初始速度 vg0 =vb0 = 0 mb = 2mg 则 p0 = 0 推开后速度 vg = 2vb p = 0 且方向相反 则 推开前后系统动量不变 p p0 = Fg Fb g v b v mg mb
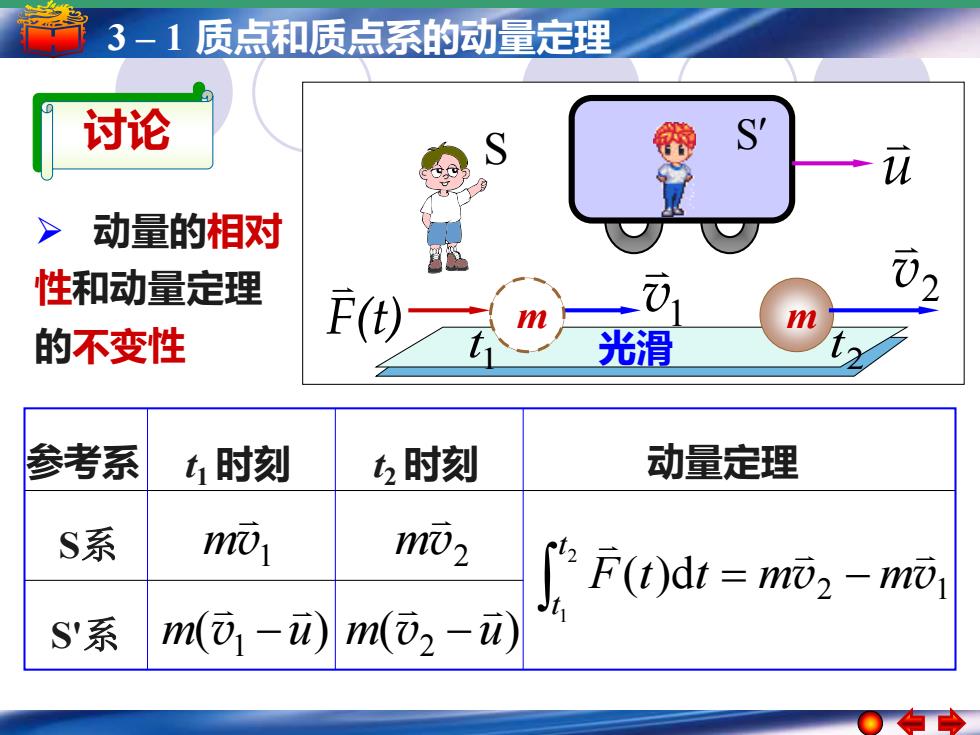
3-1质点和质点系的动量定理 讨论 > 动量的相对 性和动量定理 的不变性 F() 光滑 参考系 t时刻 时刻 动量定理 S系 mv m02 "F(t)dt mz -mo S系 m(⑦1-)m(⑦2-u)
5 3 ––11简谐运动 质点和质点系的动量定理 简谐运动的振幅 周期 频率和相位 动量定理 S系 S'系 t 参考系 t1 时刻 2 时刻 光滑 u S m v1 F(t) 1 t ➢ 动量的相对 性和动量定理 的不变性 讨论 2 1 2 1 ( )d v v F t t m m t t = − v1 m v2 m ( ) 1 m u v − ( ) 2 m u v − S m 2 v 2 t m