
Earthquake Design of Wood Structures Mar213 1.Seismic Hazards Earthquakes! Earthquakes in Canada
Earthquake Design of Wood Structures Minghao Li, Ph.D. Postdoctoral Research Fellow Timber Engineering and Applied Mechanics Group Department of Wood Science The University of British Columbia, Vancouver, BC, Canada minghao.li@ubc.ca 1-604-822-8185 March 11th, 2013 UBC, Vancouver, BC, Canada 2 Prince George, BC 3 1. Seismic Hazards 4 Earthquakes! 5 Earthquakes in Canada 6

Failure of wood buildings in earthquake quake ground motion Shake table tests on full-scale wood buildinas in Nat Earthquake Loads Equivalent static base shear M V=ST,MEWI(RR。 factor R F+F+F
Failure of wood buildings in earthquakes Northridge earthquake, California, 1994 Kobe earthquake, 1995 7 Earthquake ground motions Fault • Magnitude measures amount of energy released • Distance shaking decays with distance • Local soil conditions shaking damps in hard rock, but amplifies in soft soil 8 Shake table tests on full-scale wood buildings 9 2. Earthquake Loads & Effects in National Building Code of Canada (NBCC), 2005 10 Base shear V = F1+F2+F3 Earthquake Loads F1 = M1 .a1 F3 = M3 .a3 F2 = M2 .a2 M3 M1 M2 Ground motions 11 V = S(Ta )Mv IEW / (RdRo ) where S(Ta ) = design spectral acceleration; Ta = fundamental period; e.g., 0.05(hn ) 3/4 for wood structures with shear walls; Mv = higher mode factor; IE = earthquake importance factor; W = total building weight; Rd = ductility-related force modification factor; and Ro = over-strength related force modification factor Equivalent static base shear 12
n曲hargpoctnsa2%n50yeans Dosign spectral acceloration S(T csan Modification factor R cug Modification factorR 5 Earthquake force distribution among stories V-M ≤025V
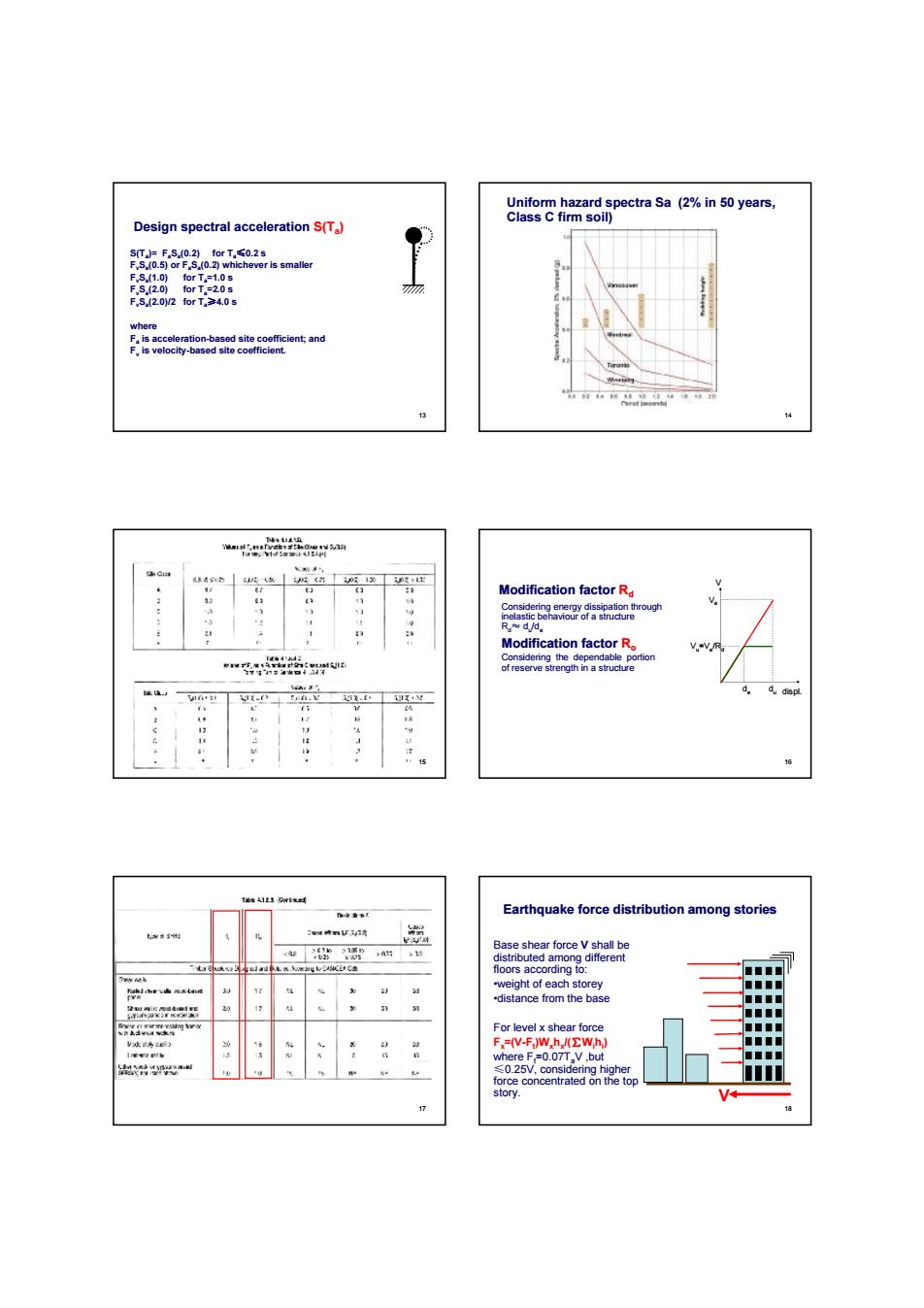
Design spectral acceleration S(Ta ) S(Ta )= FaSa (0.2) for Ta≤0.2 s FvSa (0.5) or FaSa (0.2) whichever is smaller FvSa (1.0) for Ta=1.0 s FvSa (2.0) for Ta=2.0 s FvSa (2.0)/2 for Ta≥4.0 s where Fa is acceleration-based site coefficient; and Fv is velocity-based site coefficient. 13 Uniform hazard spectra Sa (2% in 50 years, Class C firm soil) 14 15 Modification factor Rd V displ. du Ve Vu=Ve /Rd de Considering energy dissipation through inelastic behaviour of a structure Rd≈ du /de Modification factor Ro Considering the dependable portion of reserve strength in a structure 16 17 Earthquake force distribution among stories Base shear force V shall be distributed among different floors according to: •weight of each storey •distance from the base For level x shear force Fx=(V-Ft )Wxhx /(∑Wihi ) where Ft=0.07TaV ,but ≤0.25V, considering higher force concentrated on the top story. V 18

3.1 Shear walls ninSycm 美n Panel-sheathed shear walls Braced shear walls 3.2 Braced frames
3. Earthquake Force Resisting Systems 19 • Shear walls • Braced frames • Moment resisting frames • Hybrid system 3.1 Shear walls 20 Panel-sheathed shear walls Loading 21 Double sheathings and more nailed connections 22 Braced shear walls Japanese post-and-beam wood construction 23 3.2 Braced frames 24

Partial bracing Full bracing tatic tests on bolted bracing conn Reinforcement of connections 3.3 Moment resisting frames
Partial bracing 25 Full bracing 26 Static tests on bolted bracing connections Connections are critical 27 Reinforcement of connections Unreinforced connection in PSL Fibreglass reinforced connections Plywood reinforced connections Trussplate reinforced connections 28 3.3 Moment resisting frames 29 Old barn Community Centre, Vancouver, BC 30