
·部分不可约多项式表 2阶 1 7 3阶 1 13 4阶 1 23 3 37 5 07 5阶 1 45 3 75 5 67 2013/4/11 7
2013/4/11 7 • 部分不可约多项式表 2阶 1 7 3阶 1 13 4阶 1 23 3 37 5 07 5阶 1 45 3 75 5 67
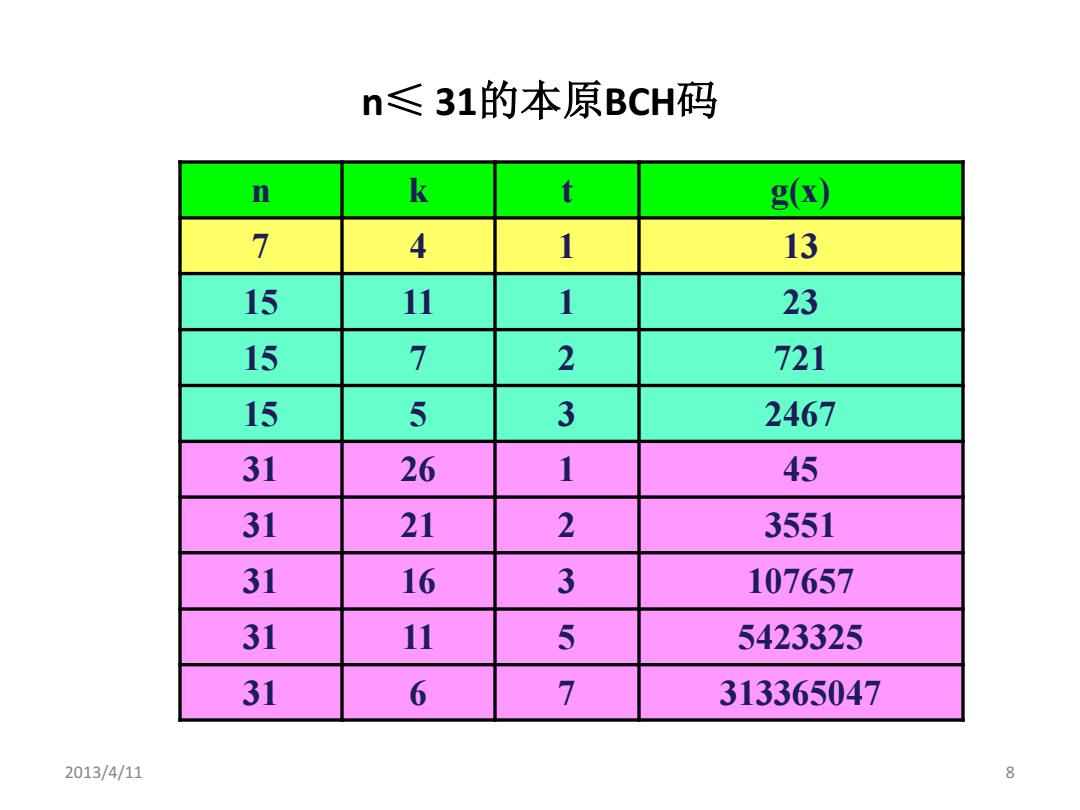
n≤31的本原BCH码 n k t g(x) 7 4 1 13 15 11 1 23 15 7 2 721 15 5 3 2467 31 26 1 45 31 21 2 3551 31 16 3 107657 31 11 5 5423325 31 6 7 313365047 2013/4/11 8
2013/4/11 8 n≤ 31的本原BCH码 n k t g(x) 7 4 1 13 15 11 1 23 15 7 2 721 15 5 3 2467 31 26 1 45 31 21 2 3551 31 16 3 107657 31 11 5 5423325 31 6 7 313365047

部分非本原BCH码 m k d g(x) 17 9 5 727 21 16 3 43 21 12 5 1663 21 6 7 126357 21 4 9 643215 23 12 7 5343 25 5 5 4102041 27 9 3 1001001 27 7 6 7007007 33 6 7 3043 2013/4/11 9
2013/4/11 9 部分非本原BCH码 n k d g(x) 17 9 5 727 21 16 3 43 21 12 5 1663 21 6 7 126357 21 4 9 643215 23 12 7 5343 25 5 5 4102041 27 9 3 1001001 27 7 6 7007007 33 6 7 3043

3.3有限域 ·一个元素个数有限的域称为有限域,或者伽罗华域(Galois field); ·有限域中元素的个数为一个素数,记为GF(p),其中p为素数; 一个大于1的整数,如果它的正因数只有1和它本身,就叫做 素数,否则就叫做合数。 ·有限域中运算满足 一交换律:a+b=b+a,ab=b"a -结合律:(a+b)+c=a+(b+c),a(bc)=(ab)c -和分配律:a·(b+c)=ab+a·c 2013/4/11 10
2013/4/11 10 3.3 有限域 • 一个元素个数有限的域称为有限域,或者伽罗华域(Galois field); • 有限域中元素的个数为一个素数,记为GF(p),其中p为素数; • 一个大于1的整数,如果它的正因数只有1和它本身,就叫做 素数,否则就叫做合数。 • 有限域中运算满足 – 交换律:a+b=b+a, a·b=b ·a – 结合律:(a+b)+c=a+(b+c),a·(b·c)=(a·b) ·c – 和分配律:a ·(b+c)=a ·b+a ·c

·可以将GF(p)延伸为一个含有pm个元素的域,称为GF(p)的扩展域,表示 为GF(pm),m是一个非零正整数。注意:GF(p)是GF(pm)的子集。 二进制域GF(2)是扩展域GF(2m)的一个子域,类似于实数域是复数域的一 个子域一样。除了数字0和1之外,在扩展域中还有特殊的元素,用一个 新的符号a表示。GF(2m)中任何非0元素都可由a的幂次表示。 ·有限元素的集合GF2m),只能含有2m个元素,并且对乘法封闭,其约束 条件为:a2m-10+1=0 ·根据这个多项式限制条件,任何幂次等于或超过2m1的域元素都可降阶为 下述幂次小于2m-1的元素: a2+m)=a2m-1a+l=a2+ ·这样,GF(2m的元素可表示为: GF(2m)={0,a°,a,a2,…,a2m-2} 11
11 • 可以将GF(p)延伸为一个含有pm个元素的域,称为GF(p)的扩展域,表示 为GF(pm),m是一个非零正整数。注意:GF(p)是GF(pm)的子集。 • 二进制域GF(2)是扩展域GF(2m)的一个子域,类似于实数域是复数域的一 个子域一样。除了数字0和1之外,在扩展域中还有特殊的元素,用一个 新的符号a表示。GF(2m)中任何非0元素都可由a的幂次表示。 • 有限元素的集合GF(2m),只能含有2m个元素,并且对乘法封闭,其约束 条件为: • 根据这个多项式限制条件,任何幂次等于或超过2m-1的域元素都可降阶为 下述幂次小于2m-1的元素: • 这样,GF(2m)的元素可表示为: 1 0 (2 1) + = − m a (2 + ) (2 −1) +1 +1 = = n n n a a a a m m (2 ) {0, , , , , } 0 1 2 2 −2 = m GF a a a a m