
第一篇热 传导 第一章导热的理论基础 本章闹述导热的理论基础。首先介绍导热的基本定律,然后,基于导热基本定律及能量守 恒定律,建立导热的微分方程,最后讨论导热问题的单值性条件及导热问题的求解方法 1.1导热基本定律 1.1.1温度场 某一物理量在空间的分布称为该物理量的场,如电场、磁场、引力场。温度在空间的分布称 为温度场。温度场有稳态温度场和非稳态温度场之分,如果温度场不随时间而变,称为稳态温 度扬:反之,称为非稳态温度场。 如果我们用r表示泛指的空间坐标,π表示时间,则稳态温度场及非稳态温度场的数学表 达式分别为 t=f(r】 (1-1) t=f(r,t) (1-2) 同一时刻,物体中由温度相同的点构成的面称为等温面,非稳态温度场的等温面可以随时 间而变化。 沿等温面的法线方向的温度变化率最大,称为温度梯度,用符号gradt表示,取等温面的 外法线方向作为温度梯度的正方向。直角坐标系中,温度梯度的表达式为 grad=嘉++2 (1-3) 上式中,jk分别表示xy、之方向的单位向量. 1.1.2导热基本定律 物体内的分子、原子及自由电子等微观粒子处于不断的热运动中,其热运动的强弱与所处 的温度有关,温度高,则热运动就强。当物体内温度分布不均匀时,微观粒子间就发生能量交 换,热量从温度较高(即热运动较强)的部分传递到温度较低(热运动较弱)的部分,这种依靠微 观粒子的热运动而产生的能量传递现象,称为热传导,简称导热.物体在导热过程中,各部分物 质不发生宏观位移。 导热现象遵循傅里叶定律。在各向同性的介质中,傅里叶定律的向量表达式为 1

q=-grad (1-4) 式中,9是热流密度(或称热通量),它是一个向量,其大小等于单位时间内通过单位等温面面 积的热量,并以等温面的外法线方向为正方向,单位是W/m入是比例系数,称为导扶系数(或 称导热率).了是nabla算子,m是法线方向的单位向量】 傅里叶定律是导热的一条基本定律。它表明,在各向同性介质中,热流密度的大小与温度 梯度成正比,其方向与温度梯度反向.由此可知,热流密度向量垂直于等温面,沿着温度降低的 方向。物体内的温度场一经确定,即可由傅里叶定律求得物体内各处的热流密度,进而求得热 量(即单位时间内的导热量)。因此,在导热问题的求解时,首先应把注意力集中于求解温度 场。 在直角坐标系中,热流密度向量可表示为 g=gi+qxi+ak (1-5)】 49表示g在,y,2方向的分量。 式(1-3)及式(1-5)代入式(1-4),得到 ,=-4爱9=-号 =-是 (1-6) 上式表明,热流密度在任一方向上的分量与该方向上的温度变化率成正比。 特别值得指出的是,上面的讨论仅对各向同性材料中的导热过程有效。 根据傅里叶定律,当物体中某处由于热扰动而使该处温度发生变化时,整个物体内的温度 分布及热流密度立刻发生变化,即使离开扰动源无限远的地方,也能马上感受到扰动的影响, 这表明,热扰动是以无限大的速度传播的,显然,这一结论有很大的局限性,声音(压力波)以声 速传播,电磁波以光速传播,热扰动也必定以一有限的速度传播,由统计热力学理论可知,热扰 动只能以有限的速度在物体内传播。因此,必须对博里叶定律作适当的修正,式(1-4)变为 是+g=-grad t (1-7) c=Val 式中,a是材料的热扩散率(或称导温系数),c是热传播速度,)称为松弛时间。在大多数实际 导热问题中,a比2小10个量级,因而式(1-7)中左边第一项与第二项相比可忽略不计,式(1 7)退化为傅里叶定律,只有在深冷时,或在热负荷急剧变化的场合,前者c的值很小,后者头很 大,式(1)左边第一项才不能忽略 1.1.3导热系数 导热系数是表征材料导热能力的物理量,单位是W/(m·K),或W/八m·℃)。它与材料 的种类及其所处的状态有关。 热物性学的现代理论提供了对导热过程微观机理的解释,并有助于材料热物性宏观测试 值的整理。但这些理论尚不完普,还不能用于精确预测材料的导热系数值,材料导热系数仍然 由专门实验测定。 傅里叶定律提供了导热系数的定义式,是由实验测定材料导热系数的基础。由式(1-4)可 得导热系数的定义式为 ·2·

A=-grad i (1-8) 在实验中,只要测定热流密度q及物体内的温度分布,就可由式(1-8)求得导热系数。 不同材料的导热系数差别极大,一般而言,纯金属的导热系数最大(纯金属中,又以银的导 热系数为最大),气体的导热系数最小.传热学教材[2]的附录中,列出了常见材料的导热系数 有关导热系数更详细的资料,可参阅文献[3~5]。 1.2各向异性材料中的导热 各个方向上导热系数都相同的材料,称为各向同性材料,此外,还有许多天然的或人造的 材料,其导热系数随方向而变化,这样的材料称为各向异性材料。例如石英、木材,石墨、层压 板,玻璃钢等。木材中,在顺木纹、垂直于木纹以及环绕木纹的三个方向上,导热系数是各不相 同的,各向异性材料中的热传导理论在科学和技术的各个领域里起着重要作用,但这方面的成 梁却十分有限。本教材中,仅涉及其最基础的内容。 各向异性材料与各向同性材料相比,其导热过程有两个重要的差别。其一,各向异性材料 沿各个方向的导热系数是不同的。其二,各向异性材料在某一方向上的热流密度分量不仅与该 方向上的温度变化率有关,而且还与其垂直方向上的温度变化率有关。在直角坐标系(红,x, )中,沿三个坐标轴方向的热流密度分量可表示为 =-毫一毫- (1-9a) m=-知是-是费 (1-9b (1-9c〉 以上三式可概括成如下的表达式 -名毫 =1,2,3 (1-10) 式中,入表示j方向上的单位温度变化率在方向上引起的热流密度的大小,反映了材科的定 向导热性能,称为导热系数分量.。根据不可逆过程热力学中的翁萨格原理(Onsagar'sprinci, ples),导热系数分量服从互易关系们 入y=i,j=1,2,3 (1-11a) 以外,正如文献[15]所述,根据不可逆热力学,有 >0 =1,2,3 (1-11b) 而且,系数,(≠》的大小被下述要求所限制 入·w-得>0≠j (1-11c) 导热系数的方向性使得各向异性材料中的导热规律复杂化了,但是,如果恰当地选择坐标 系(数学上通过矩阵的初等变换),一定可以找到 个坐标系(台,,),在(,,6)坐标系 中,沿(=1,2,3)方向的热流密度分量只与该方向上的温度变化率有关,而与其他两个方向 上的温度变化率无关。即 3
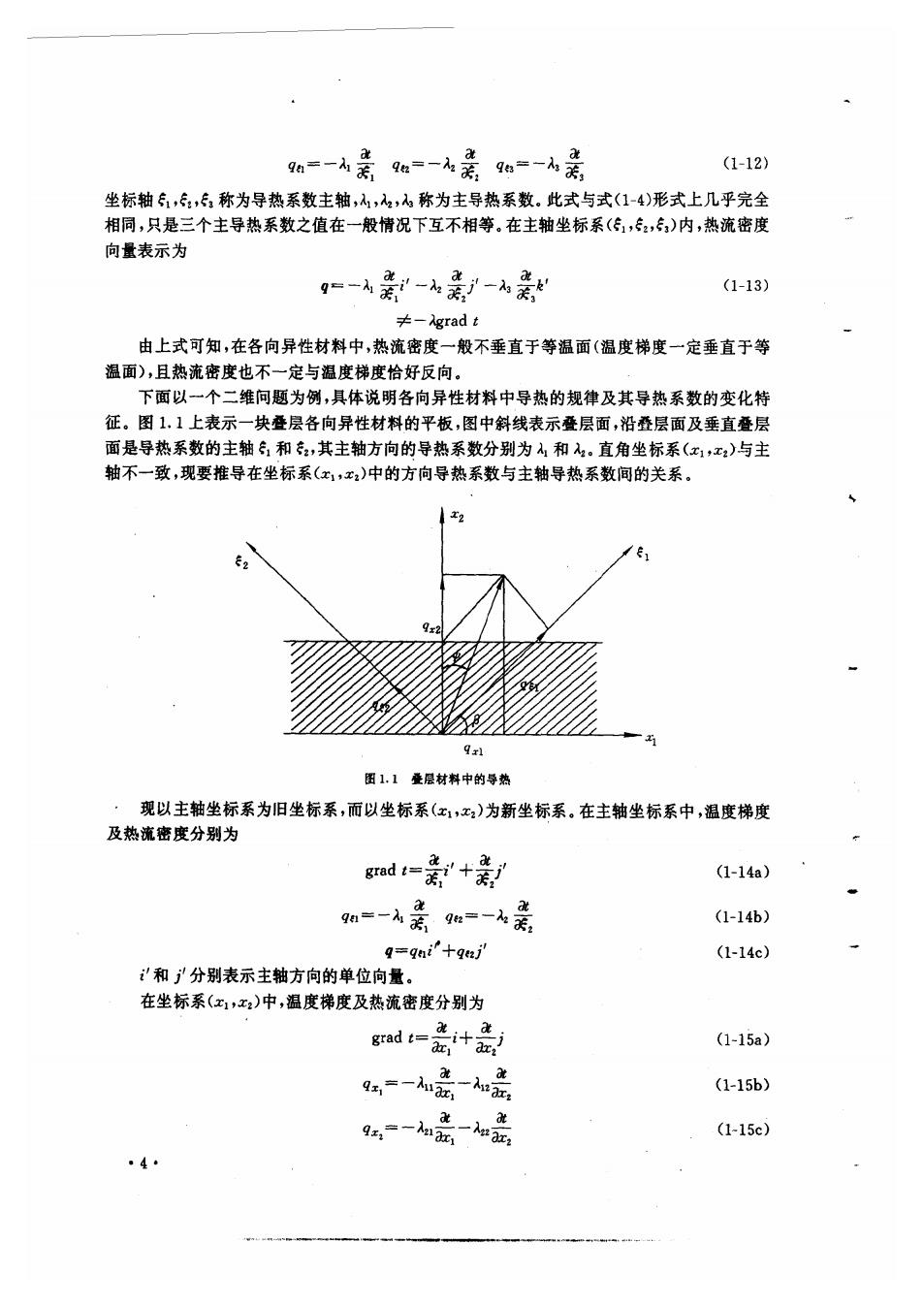
9a=-毫a=-4是96=-4爱 (1-12 坐标轴行,6,6称为导热系数主轴,4,2,d称为主导热系数.此式与式(1-4)形式上几乎完全 相同,只是三个主导热系数之值在一般情况下互不相等在丰轴坐标系(,,,,)内,热流密摩 向量表示为 g=-4-4影- (1-13) ≠-grad t 由上式可知,在各向异性材料中,热流密度一般不垂直于等温面(温度梯度一定垂直于等 温面),且热流密度也不 定与温度梯度恰好反向。 下面以一个二维间问题为例,具体说明各向异性材料中导热的规律及其导热系数的变化特 征。图1,1上表示一块叠层各向异性材料的平板,图中斜线表示叠层面,沿叠层面及垂直叠层 面是导热系数的主轴6和,其主轴方向的导热系数分别为和.直角坐标系(红1)与主 轴不一致,现要推导在坐标系(x,x)中的方向导热系数与主轴导热系数间的关系。 9x1 图1.1曼层材料中的导热 ,现以主轴坐标系为旧坐标系,而以坐标系(x1,x)为新坐标系。在主轴坐标系中,温度梯度 及热流密度分别为 gad=爱+割 (1-14a) ga=-名毫9如=-4毫 (1-14b) q=qni'+qnj (1-14c) '和分别表示主轴方向的单位向量。 在坐标系(x)中,温度梯度及热流密度分别为 gadt=斋+ (1-15a) =一毫-爱 (1-15b) %,=-是- (1-15c) 4…

q=qi十q,Jj (1-15d) 同一物体中,温度梯度及热流密度与坐标系无关。由此,可以得到 9z-qe,cosB-9e,sinB (a) 94,=9%,sinf+q4,cos月 (6) 是-cos9-毫in9 (c) 是-素in+毫eop (d) (c)和(d)联立,可解得 是-是cosg+盖sinA (e) 亮一孟inB+是cosA ( 式(e)和式(D代人式(a),得到 a=-A去coap+ingco+A-密in+宽co)in (co()sinco (1-16a) 同理可得 (1-16b) 比较式(1-15b)、(1-15c)和式(1-16a)、(1-16b),得 Au=(Aicos'B+Asin"B) (1-17a) Au==(-)sinBcos月 (1-17b) n=(Asin'8+Acos"B) (1-17c) 式(117)告诉我们,各向异性材料的导热主轴及主轴方向导热系数知道后,任何方向上的 导热系数就能算出, 如果使图1.】所示叠层平板的两表面维持常温t和2,则平板中将产生一维稳态温度 杨4=毫=0此时。 94=-(a-名os6in9是 (1-18a) 4,=-(sim+4 (1-18b) 热流密度与x轴的夹角的正切为 9x1(入1-入2)sinBcos月 g-g2,-5im8+4cos币 (1-19) 显然,若能满足以下两个条件,则中=0,或热流密度的方向与等温面法线方向一致:(1)入= ,即材料为各向同性;或(2)B=0,即坐标系(红1,x)与主轴一致, 对各向异性材料来说,即使取主轴坐标系,热流密度并不与等温面垂直,而温度梯度总是 沿等温面的法线方向 5