
在本书以后的讨论中,只讨论各向同性材料中的导热。 1.3导热方程 傅里叶定律揭示了物体中任意位置处热流密度与该处温度梯度间的关系。如果把能量守 恒定律与傅里叶定律结合起来,就能得到导热方程。导热方程是所有导热过程所必须遵循的, 它可以以积分方程或微分方程的形式表示,本节中仅论述导热微分方程。 在直角坐标系中的导热微分方程,许多传热学教材中都有推导[2],这里直接引用其推导 结果 是(oc)=7(A7)+g (1-20) 式中,c是材料的比热,P是密度,q,是体积发热率, 常物性时,式(1-20)变为 -7+受 (1-21) 上式中,a=A/(p)称为热扩散率,它也是一个重要的热物性参数,表征材料在非稳态导热过程 中扩散热量的能力,其值可由物性表中查得。不同材料的热扩散率差别极大,油的扩散率为 1×10'm/s,而银的扩散率可达2×10-m'/s。式中,等号左边称为非稳态项,等号右边第 项称为扩散项,第二项称为热源项。 无内热源时,9.=0,式(1-21)简化为 -4 (1-22) 上式背称为傅里叶导热微分方程,它是一个典型的抛物线型偏微分方程 对于稳态导热问题,非稳态项消失,式(1-21)简化为 t+=0 (1-23) 上式称为泊桑方程 对于无内热源的稳态导热向题,上式可进一步简化为 71=0 (1-24) 上式称为拉普拉斯方程,它是典型的椭圆型偏微分方程。 在求解实际导热问题时,所遇到的物体的几何形状是各式各样的,为了使该问题易于求 解,往往对不同的具体问题采用不同的坐标系,以尽可能减少导热方程中自变量的数目,或使 边界条件的表达简化。下面,我们推导任意正交坐标系中的导热微分方程。 任意正交坐标系中导热方程的推导,可以采用控制容积内的能量平衡法,也可通过不同正 交坐标系中基本量(单位向量、梯度等)的关系,由直角坐标系中的导热微分方程转换而得). 这里采用第一种方法。 图1.2表示一个正交坐标系(,,x),x1x,西是它的坐标轴,它与直角坐标xyz的 函数关系为 6
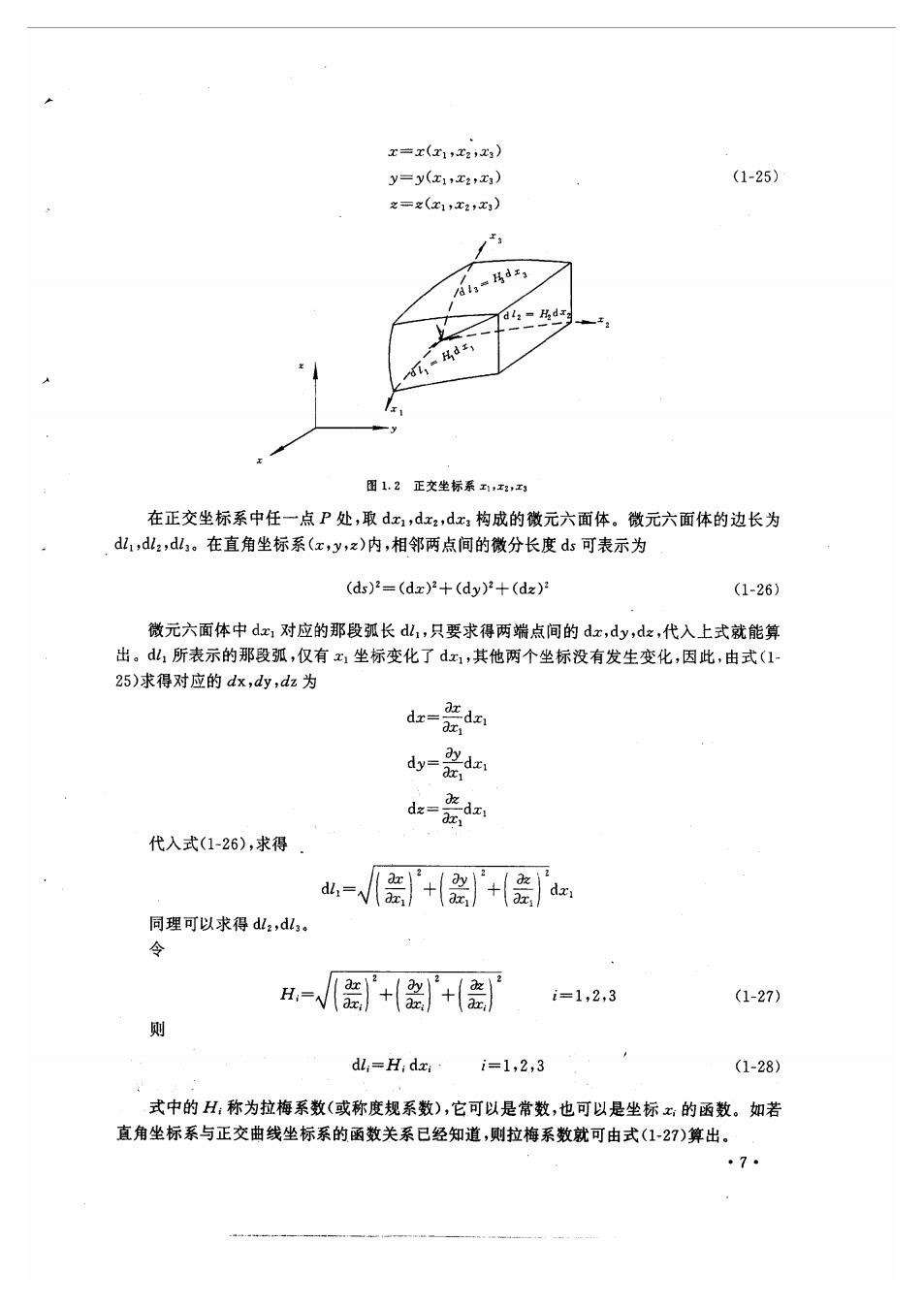
x=x(红1xz) y=y() (1-25) =z(1xx) 田1,2正交坐标系4 在正交坐标系中任一点P处,取dx1,dx,dx构成的徽元六面体。徽元六面体的边长为 dl1,dl:,d山。在直角坐标系(x,yz)内,相邻两点间的微分长度ds可表示为 (d)2=(dx2+(dy+(dx) (1-26) 徽元六面体中对应的那段到长d山,只要求得两端点间的dx,dy,dz,代入上式就能算 出。山,所表示的那段弧,仅有x坐标变化了d,其他两个坐标没有发生变化,因此,由式(1 25)求得对应的dx,dy,dz为 dd dy d ded 代入式(1-26),求得 d出,=√++ 同理可以求得d,d H=√(++ i=1,2,3 (1-27) dl,=H,dx·i=1,2,3 (1-28) 式中的H,称为拉梅系数(或称度规系数),它可以是常数,也可以是坐标云的函数。如若 直角坐标系与正交曲线坐标系的面数关系已经知道,则拉梅系数就可由式(1-27)算出。 7

山:求得后,就可求得微元六面体各个面的面积及其体积,它们是 dA=dl·dl,=H·H,·dz·dx, dA2=dh·dh=H1·H,·dx1·dx (1-29) dA=d·d=H1·H·d·dr dA=Hd·d·dx(H·dx) i=1,2,3 dw=d,·d,·d,=H·dx1·dx4·dx1 式中H=H1·H2·H,。 由微元六面体的能量平衡,可以写出如下热平衡式: 导入控制容积的净热流量十控制容积内热源发热量=控制容积内内能增量 对各向同性材料,导入净热量为 含-毫A-[-受A-引毫A出,]} =名引毫Ad出, -名引景品dd 控制容积内热源发热量为 g.·dw=g,·H·dx1·dx2·dx 单位时间内控制容积内能增量为 dHdrd 代入热平衡式,经整理后得到 四-这引昂+m (1-30) 上式即为变物性时正交坐标系中导热微分方程的表达式.在不同的具体条件下,式(1-30) 可以简化。 常物性时,简化为 县亲=名是+ (1-31) 常物性稳态导热,简化为 名品)+贤=0 (1-32) 对于稳态导热而言,温度场及等湿面均不随时间而变化。因此,如果把正交曲线坐标的 两个坐标轴x,放在等温面上(x4,互相正交),坐标轴与等温面垂直,温度扬戒为 维温度场t=(),问题在于,温度场本身是求解的目标,在一般情况下,等温面必须要在油 度场解出后才能知道,所以在温度场解出前,能把温度场简化为一维问题的正交坐标系是无 8
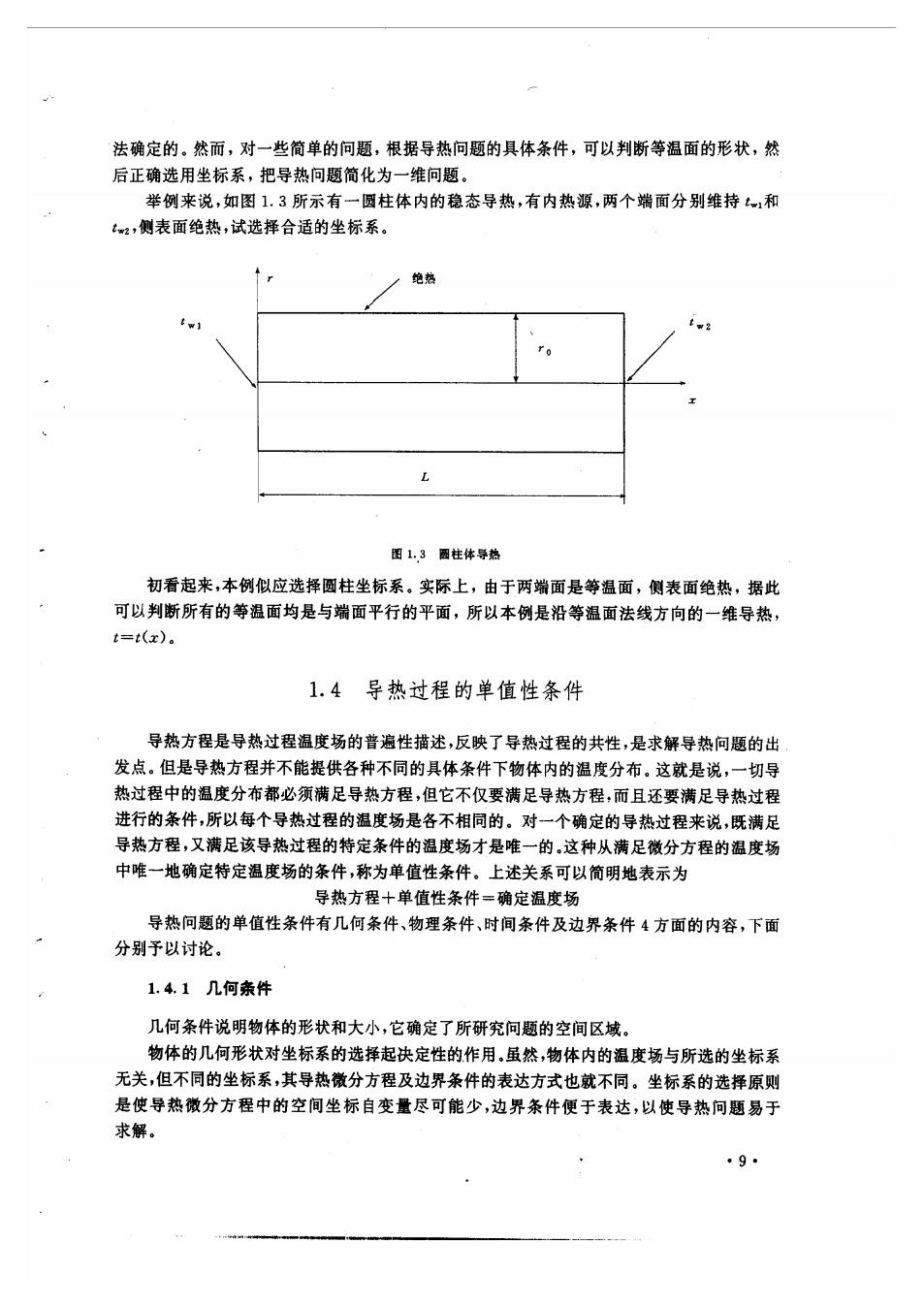
法确定的。然而,对一些简单的问题,根据导热问题的具体条件,可以判断等温面的形状,然 后正确选用坐标系,把导热问题简化为一维问题。 举例来说,如图1.3所示有一圆柱体内的稳态导热,有内热源,两个端面分别维持,和 t,侧表面绝热,试选择合适的坐标系。 绝热 图1,3西柱体导热 初看起来,本例似应选择圆柱坐标系。实际上,由于两端面是等温面,侧表面绝热,据此 可以判断所有的等温面均是与端面平行的平面,所以本例是沿等温面法线方向的一维导热 =(x). 1.4导热过程的单值性条件 导热方程是导热过程温度场的普遍性描述,反映了导热过程的共性,是求解导热问题的出 发点。但是导热方程并不能提供各种不同的具体条件下物体内的温度分布。这就是说,一切导 热过程中的温度分布都必须满足导热方程,但它不仅要满足导热方程,而且还要满足导热过程 进行的条件,所以每个导热过程的温度场是各不相同的。对一个确定的导热过程来说,既满足 导热方程,又满足该导热过程的特定条件的温度场才是唯一的,这种从满足微分方程的温度场 中唯一地确定特定温度场的条件,称为单值性条件。上述关系可以简明地表示为 导热方程十单值性条件=确定温度场 导热问题的单值性条件有几何条件、物理条件,时间条件及边界条件4方面的内容,下面 分别子以讨论 1.4.1几何条件 几何条件说明物体的形状和大小,它确定了所研究问题的空间区域。 物体的几何形状对坐标系的选择起决定性的作用,虽然,物体内的温度场与所选的坐标系 无关,但不同的坐标系,其导热微分方程及边界条件的表达方式也就不同。坐标系的选择原则 是使导热微分方程中的空间坐标自变量尽可能少,边界条件便于表达,以使导热问题易于 求解 .9

1.4.2物理亲件 物理条件包括材料的热物性及有无内热源。原则上材料的热物性分为常物性及变物性两 类,严格意义上的常物性材料是没有的变物性时需要知道热物性随温度的变化关系,变物性 给温度场的求解带来很大困准,求解温度场时需要知道物性,而物性又取决于温度,这是温度 场和物性场耦合的求解问题,只有极少数变导热系数的导热问题,可以通过适当的变换而求得 分析解,对变物性导热问题最简便的处理方法,是以物性的某个平均值(如算术平均值)代替变 物性,然后按常物性的导热问题求解,这样处理,会给解得的温度场带来一定的误差,它仅适用 于材料物性在所研究的温度范围内变化不大,或对解的精确度要求不高的场合, 本书只讨论导热问题的分析解法,因此主要研究常物性导热问题。变物性的导热问题, 般可用数值法求解。 几何条件及物理条件确定后,微分方程的具体形式完全被确定了,这样的方程,在数学领 域称为泛定方程,如前面提及的拉普拉斯方程,泊桑方程及热传导方程等数理方程这门课,就 是专门研究这些泛定方程求解的。 1.4.3时间条件 时间条件说明导热过程在时间上进行的特点。如果物体内的温度场是稳态温度场,导热过 程不随时间面变,时间就不是独立变量,导热方程中没有瞬态项,反之,非稳态导热的导热方程 中就有瞬态项。我们所处的环境连续不断地在变化,所有的热过程都受到其影响,因此严格意 义上的稳态导热是不存在的。稳态导热是相对的。 瞬态导热是非稳态导热的一种重要形式。瞬态导热的特点是边界条件及内热源不随时间 而变,而在过程起始时刻,物体内的温度场与该边界条件下的稳定温度场有差异,从而使物体 内的温度随时间而变化,当时间足够长时,物体内的温度分布达到该边界条件下的稳态温度 场。在过程开始时刻物体内的温度分布称为初始条件。瞬态导热是由于初始条件与同样条件 下的稳态温度场的差异而引起的,随着时间的推移,物体内的温度场与稳态温度场间的差异越 来越小。由此可知,对于有限大的物体而言,初始条件的影响只在一定时间内起作用 如果边界条件及(或)内热源随时间而变,那末物体内的温度场不可能达到稳定,但初始茶 件对温度场的影响仍只能在一有限时间内起作用,时间足够长后,温度场仅随边界条件或内热 源的变化而变。这种只依赖于边界条件或内热源的非稳态温度场,称为准稳态温度场。 综上所述,时间条件规定三方面内容: (1)过程是稳态过程或非稳态过程 (2)非稳态过程给出初始条件. (3)边界条件及内热源随时间的变化关系。 1.4.4边界条件 我们所研究的物体总是处于一定环境中,该物体与外部环境之间的换热条件称为边界条 件。物体内的导热过程和该物体与环境间的换热过程是互相影响的,因此,物体内的导热过程 和物体与环境间的换热组成一个耦合何题,严格地说,应将物体内的导热过程和它与外部环境 间的换热过程统一处理,以确定物体的温度扬,这样做,可以使温度场的解更符合实际,但它会 10