
第三讲晶体中的晶面和晶体投影 固体结构内容可能有些抽象和枯燥,但这些是 结晶学的一把钥匙。只有掌握了基本的规律 瑰丽多彩的结构之门才会打开。欣赏美丽的宝 石,归纳晶体的结构模型,探索结构性质与其 迷人外貌间的关系,都从此开始
第三讲 晶体中的晶面和晶体投影 固体结构内容可能有些抽象和枯燥,但这些是 结晶学的一把钥匙。只有掌握了基本的规律, 瑰丽多彩的结构之门才会打开。欣赏美丽的宝 石,归纳晶体的结构模型,探索结构性质与其 迷人外貌间的关系,都从此开始
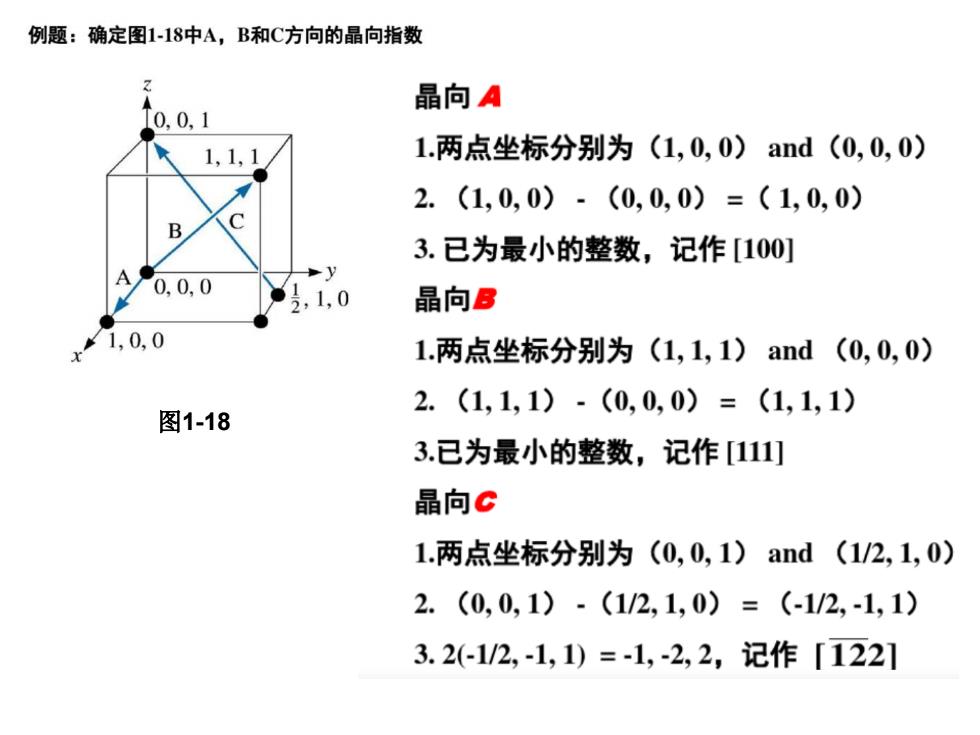
例题:确定图1-18中A,B和C方向的晶向指数 晶向A 0,0,1 1,1,1 1.两点坐标分别为(1,0,0)and(0,0,0) 2.(1,0,0)-(0,0,0)=(1,0,0) B 3.已为最小的整数,记作[100] A 。y 0.0.0 ,1,0 晶向B 1,0,0 1.两点坐标分别为(1,1,1)and(0,0,0) 2.(1,1,1)-(0,0,0)=(1,1,1) 图1-18 3.已为最小的整数,记作[111] 晶向G 1.两点坐标分别为(0,0,1)and(1/2,1,0) 2.(0,0,1)·(1/2,1,0)=(-1/2,-1,1) 3.2(-1/2,-1,1)=-1,-2,2,记作[1221
图1-18

上节课内容回顾 2.1.1空间点阵和晶胞 2.1.2晶向指数和晶面指数
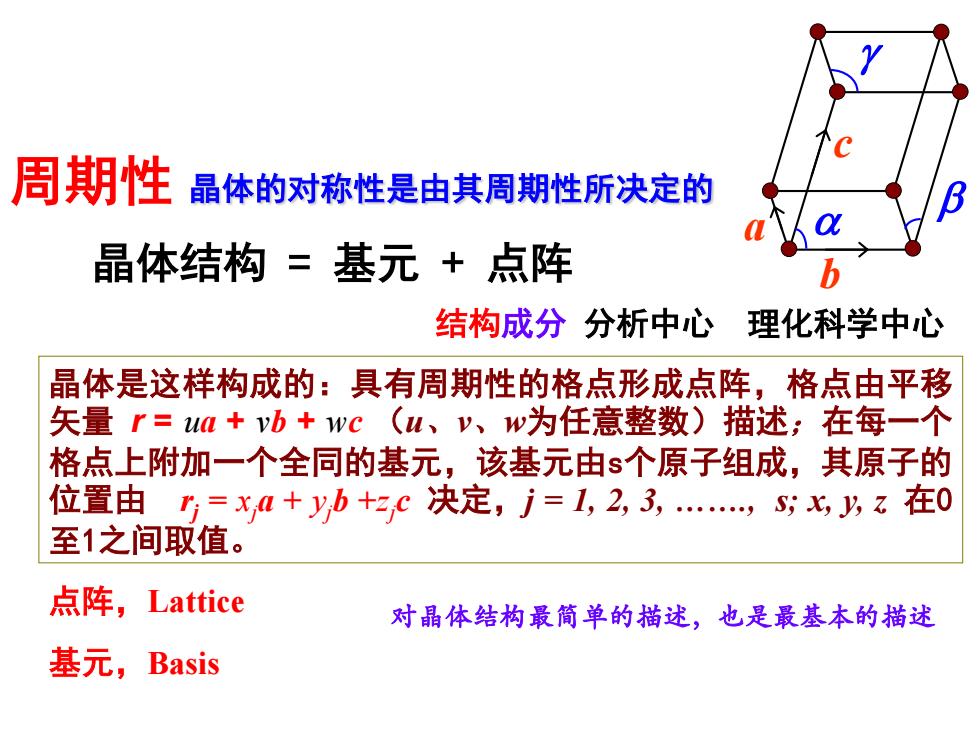
周期性晶体的对称性是由其周期性所决定的 晶体结构=基元+点阵 结构成分分析中心 理化科学中心 晶体是这样构成的:具有周期性的格点形成点阵,格点由平移 矢量r=uM+vb+wc(u、v、w为任意整数)描述;在每一个 格点上附加一个全同的基元,该基元由s个原子组成,其原子的 位置由1=x0+yb+c决定,j=1,2,3,Sx,乃z在0 至1之间取值。 点阵,Lattice 对晶体结构最简单的描述,也是最基本的描述 基元,Basis
周期性 晶体的对称性是由其周期性所决定的 点阵,Lattice 基元,Basis 晶体结构 = 基元 + 点阵 晶体是这样构成的:具有周期性的格点形成点阵,格点由平移 矢量 r = ua + vb + wc (u、v、w为任意整数)描述;在每一个 格点上附加一个全同的基元,该基元由s个原子组成,其原子的 位置由 rj = xja + yjb +zj c 决定,j = 1, 2, 3, ., s; x, y, z 在0 至1之间取值。 对晶体结构最简单的描述,也是最基本的描述 结构成分 分析中心 理化科学中心 a b c

理解概念第二讲晶体中的点、线、面 点阵(lattice)和结构基元 将重复单元看作一个点,这些点构成一个点阵。 点阵:连结其中任意两点可得一向量,将各,点 按此向量平移能复原的一组无限的点称 为点阵。 点阵点:点阵中所有的点(抽象的)称点阵点, 也称阵,点。等同点 结构基元:点阵中点的具体内容, 或周期重复的最小单位。 晶体结构=点阵+结构基元
等同点 理解概念 第二讲 晶体中的点、线、面