第九讲14种布拉菲格子 旋转对称性 晶系、参考轴 满足点阵条件+晶系不变 初基P单胞(6) 有心化 P点阵中高对称位置加心(体心N, 全面心F,单面心A,B或C双面心) 六方格子特殊心→菱形(三方)单胞 新的点阵 14种布拉菲点阵 (有心8种) 旋转对称性
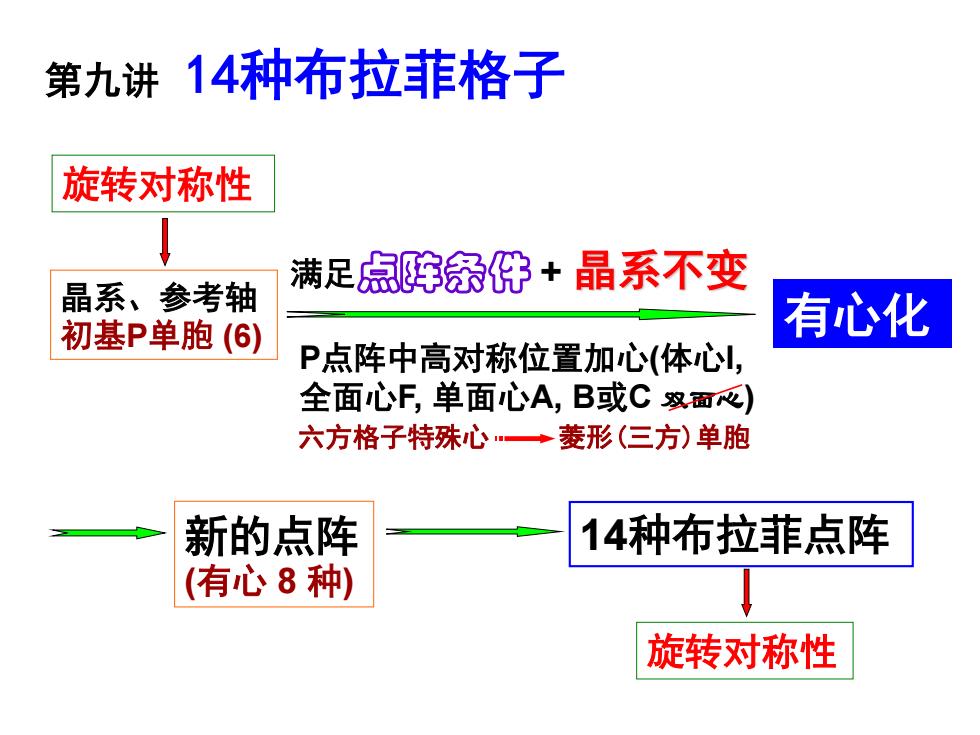
第九讲 14种布拉菲格子 旋转对称性 晶系、参考轴 初基P单胞 (6) 有心化 新的点阵 (有心 8 种) 满足点阵条件 + 晶系不变 14种布拉菲点阵 旋转对称性 P点阵中高对称位置加心(体心I, 全面心F, 单面心A, B或C 双面心) 六方格子特殊心 菱形(三方)单胞
这14种型式最早(1866年) 由Bravias(布拉菲)推得 布拉菲群和和布拉菲点阵 ,又称为布拉维点阵或布拉 加“心” 维点阵型式。 各阵点周围环境相同 x 简单:P 底心:C 侧心:A、B 体心:I 面心:F 不存在两心同时的可能
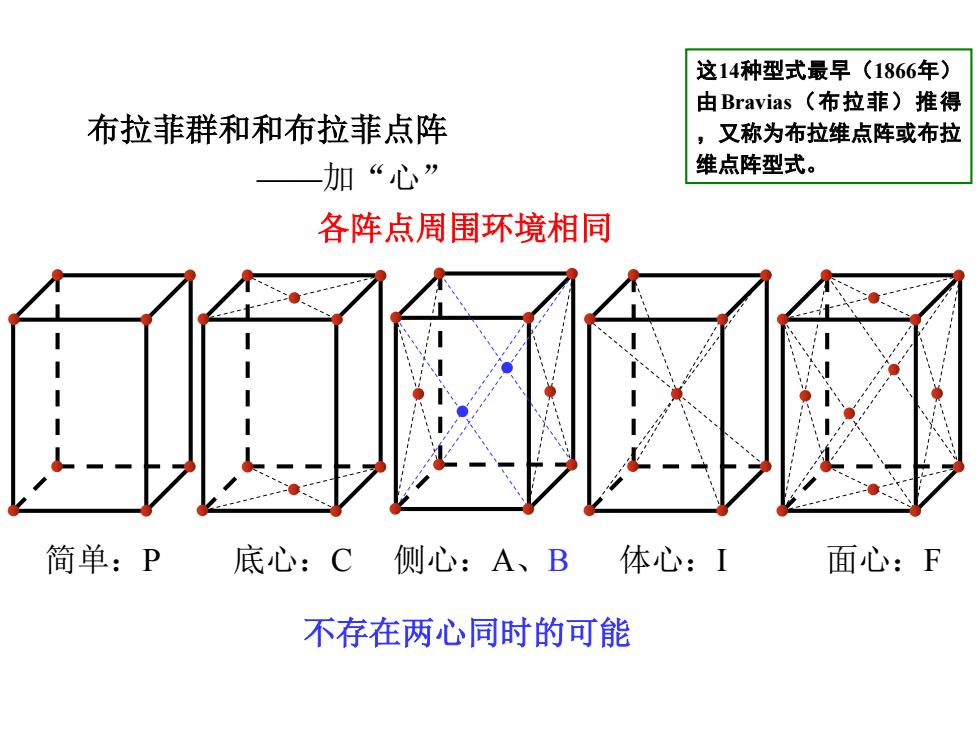
布拉菲群和和布拉菲点阵 ——加“心” 简单:P 底心:C 侧心:A、B 体心:I 面心:F 不存在两心同时的可能 各阵点周围环境相同 这14种型式最早(1866年) 由Bravias(布拉菲)推得 ,又称为布拉维点阵或布拉 维点阵型式

P点阵中高对称位置加心(体心,全面心F, 单面心A,B或C双画心) 双面心不满足点阵条件!
A B X X X X 双面心不满足点阵条件! P点阵中高对称位置加心(体心I, 全面心F, 单面心A, B或C 双面心)

三斜晶系 三斜P 单斜C=P 单斜晶系 ⊕ 单斜B=I=F=A 单斜P 单斜B
三斜晶系单斜晶系 三斜 P 单斜 P 单斜 B 单斜 C = P 单斜 B = I = F = A

正交晶系 正交C=A=B 丰P 正交P 正交0 正交 1 正交F
正交 P 正交 C 正交 I 正交 F 正 交 晶 系 正交 C = A = B ≠ P