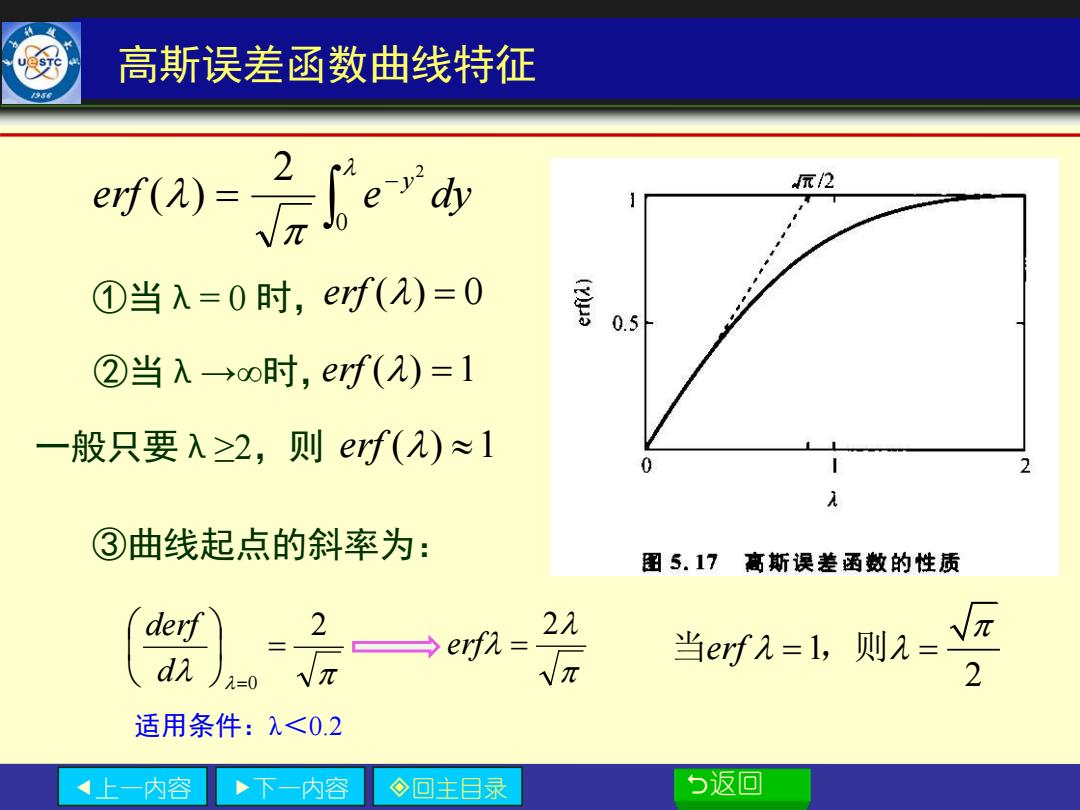
高斯误差函数曲线特征 元2 ①当入=0时,erf(2)=0 0.5 ②当入→oo时,erf(2)=1 一般只要入≥2,则erf()≈1 0 ③曲线起点的斜率为: 图5.17高斯误差函数的性质 derf 2元 当ef元=1,则= 2 适用条件:入<0.2 上一 内容 ·下一内容 ◇回主目录 5返回
上一内容 下一内容 回主目录 返回 高斯误差函数曲线特征 ①当λ= 0 时, erf () = 0 ②当λ→∞时, erf () = 1 一般只要λ≥2,则 erf () 1 ③曲线起点的斜率为: 2 0 = d = derf 2 erf = 适用条件:λ<0.2 1 2 erf 当 = = ,则 − = 0 2 2 erf ( ) e dy y
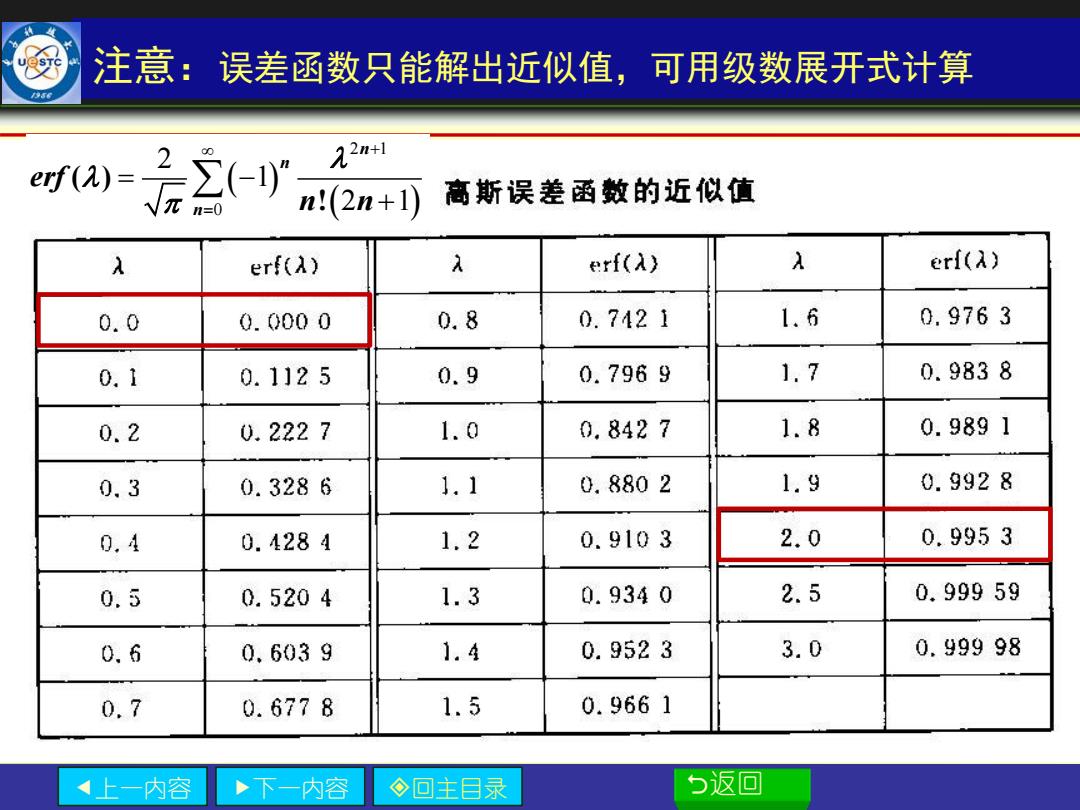
注意:误差函数只能解出近似值,可用级数展开式计算 a=2-ur 22m+刊 (2n+) 高斯误差函数的近似值 erfλ) 入 erf(入) A erf(A) 0.0 0.0000 0.8 0.7421 1.6 0.9763 0.1 0.1125 0.9 0.7969 1.7 0.9838 0.2 0.2227 1.0 0.8427 1.8 0.9891 0.3 0.3286 1.1 0.8802 1.9 0.9928 0.4 0.4284 1.2 0.9103 2.0 0.9953 0.5 0.5204 1.3 0.9340 2.5 0.99959 0.6 0.6039 1.4 0.9523 3.0 0.99998 0.7 0.6778 1.5 0.9661 上一内容 ·下一内容 ◇回主目录 5返▣
上一内容 下一内容 回主目录 返回 注意:误差函数只能解出近似值,可用级数展开式计算 ( ) ( ) 2 1 0 2 1 2 1 ( ) ! n n n erf n n + = = − +
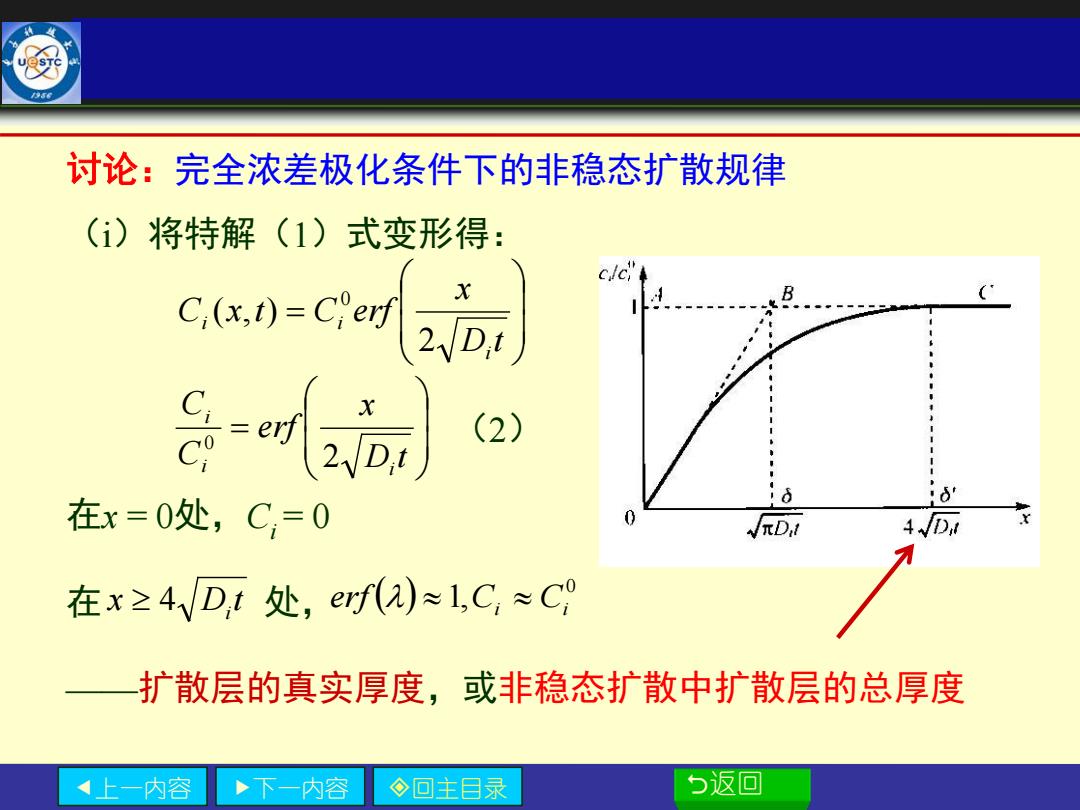
讨论:完全浓差极化条件下的非稳态扩散规律 (i) 将特解(1)式变形得: C,(x,1)=Cerf 2VD,1 8听】 (2) 在x=0处,( C √πDd 在x≥4VD,t处,erf()≈1,C,≈C0 扩散层的真实厚度,或非稳态扩散中扩散层的总厚度 内容 ·下一内容 ◇回主目录 5返回
上一内容 下一内容 回主目录 返回 讨论:完全浓差极化条件下的非稳态扩散规律 (ⅰ)将特解(1)式变形得: (2) 在x = 0处,Ci = 0 在 处, ——扩散层的真实厚度,或非稳态扩散中扩散层的总厚度 = D t x erf C C i i i 2 0 x D t 4 i ( ) 0 1,Ci Ci erf = D t x C x t C erf i i i 2 ( , ) 0
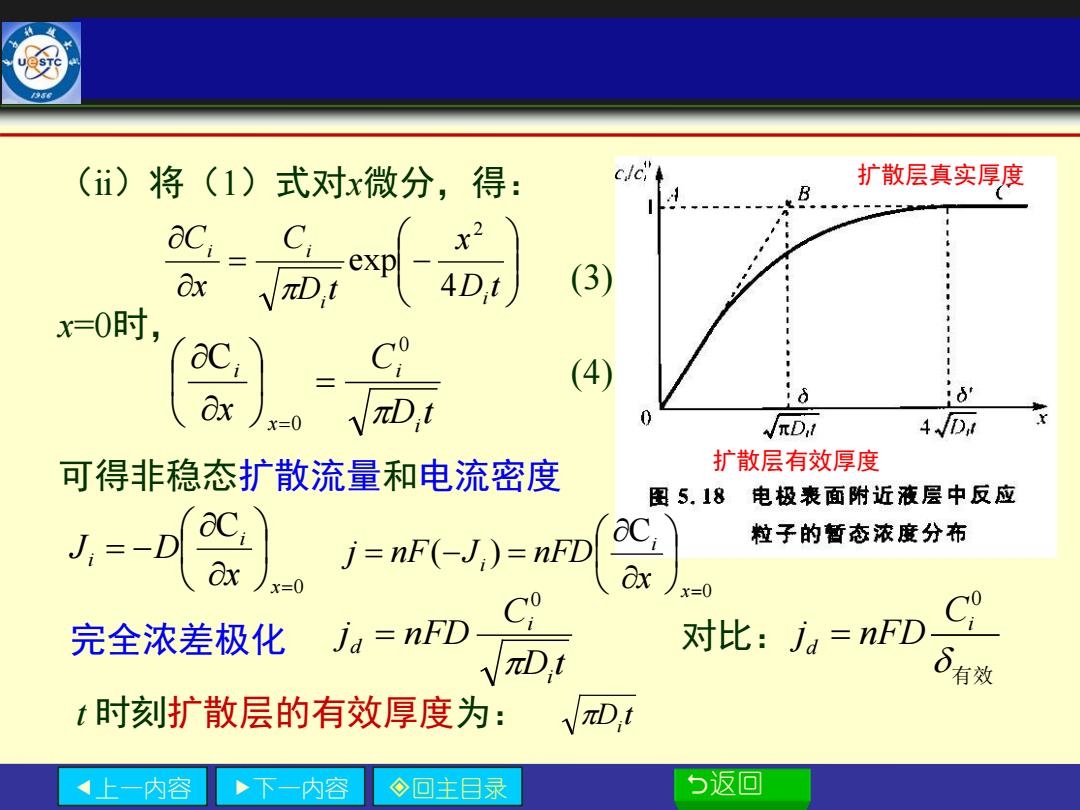
(i)将((1)式对x微分,得: c/c 扩散层真实厚度 Ox (3) x=O时, aC; (4) x-0 0 √πD1 4JD 可得非稳态扩散流量和电流密度 扩散层有效厚度 图5.18 电极表面附近液层中反应 J,=-D x 广=nF(-J)=nD C. 粒子的暂态浓度分布 x=0 8x x=0 完全浓差极化ja=nFD 对比:j4=nFD 有 t时刻扩散层的有效厚度为:√D,t 内容 下一内容 ◇回主目录 5返回
上一内容 下一内容 回主目录 返回 (ⅱ)将(1)式对x微分,得: (3) x=0时, (4) 可得非稳态扩散流量和电流密度 t 时刻扩散层的有效厚度为: = − D t x D t C x C i i i i 4 exp 2 D t C x i i x i 0 0 C = = D t i 0 C = = − x i i x J D 0 C ( ) = = − = x i i x j nF J nFD D t C j nFD i i d 0 = 扩散层有效厚度 扩散层真实厚度 完全浓差极化 0 i d C j nFD = 有效 对比: