
133822.56-100000=33822.56元。 银行储蓄存款业务中,有一种零存整取和一种整存零取。前者是每月(或每周、每年) 按同一的金额存入,到约定的期限本利和一次取出。其算式为: 4=Px(+r)-1-P 其中,P代表每月(或每周、每年)存入的金额。即如于几十年以内需要支出2万元,估 计月利率比如说为0.8%,那末每月存入100元即可达到这个数量(确切数为20181.92元)。 后一种整存零取则指一次存入若干金额的货币,在而后的预定期限内,每月(或每周、 每年)提取同等金额的货币,当达到最后期限的一次提取时,本利全部取清。其算式为: A=Px0+r)”-1 r×(1+r)” 式中的P代表每月(每周或每年)提取的金额。假如希望在10年内每月提取100元作为生 活费,估计月利率比如说也为0.8%,那末现在只需要存入7700元(确切数为7695.52元)即 可。 这两个算式都有广泛的用途。如在设计折旧提存方案、退休养老基金方案等很多方面时, 或许要利用其中某一算式,或需两个算式结合使用。很明显,这两个算式都是根据复利公式: A=P(1+)”推衍出来的,这也从一个侧面说明:复利范畴在经济生活中广泛存在。 (二)现值、终值及其运用 现值与终值的计算是现实经济生活中经常使用的方法,特别是在投资项目的评估中要 经常使用。由于利息成为收益的一般形态,所以任何一笔货币金额,不论将作怎样的运用, 甚至还没有考虑将作怎样的运用,都可根据利率计算出在未来的某一时点上,将会是一个怎 样的金额。这个金额就是前面说的本利和,也通称为“终值”,但是习惯上,终值都是由复 利计算来的。如果我们这个过程倒转过来,在确定未来某一时点上有一定金额的货币,只要 把它看作是那时的本利和,就可按现行利率计算出要能取得这样金额的本利和在现在所必须 具有的本金。这个逆算出来的本金称为“现值”。现值计算公式是由终值计算公式倒推出 来的 P= 4-7 (1+r)" 6
6 133822.56-100000=33822.56元。 银行储蓄存款业务中,有一种零存整取和一种整存零取。前者是每月(或每周、每年) 按同一的金额存入,到约定的期限本利和一次取出。其算式为: 1 (1 ) 1 n r A P P r + + − = − 其中,P代表每月(或每周、每年)存入的金额。即如于几十年以内需要支出2万元,估 计月利率比如说为0.8%,那末每月存入100元即可达到这个数量(确切数为20181.92元)。 后一种整存零取则指一次存入若干金额的货币,在而后的预定期限内,每月(或每周、 每年)提取同等金额的货币,当达到最后期限的一次提取时,本利全部取清。其算式为: (1 ) 1 (1 ) n n r A P r r + − = + 式中的P代表每月(每周或每年)提取的金额。假如希望在10年内每月提取100元作为生 活费,估计月利率比如说也为0.8%,那末现在只需要存入7700元(确切数为7695.52元)即 可。 这两个算式都有广泛的用途。如在设计折旧提存方案、退休养老基金方案等很多方面时, 或许要利用其中某一算式,或需两个算式结合使用。很明显,这两个算式都是根据复利公式: (1 )n A P r = + 推衍出来的,这也从一个侧面说明:复利范畴在经济生活中广泛存在。 (二)现值、终值及其运用 现值与终值的计算是现实经济生活中经常使用的方法,特别是在投资项目的评估中要 经常使用。由于利息成为收益的一般形态,所以任何一笔货币金额,不论将作怎样的运用, 甚至还没有考虑将作怎样的运用,都可根据利率计算出在未来的某一时点上,将会是一个怎 样的金额。这个金额就是前面说的本利和,也通称为“终值”,但是习惯上,终值都是由复 利计算来的。如果我们这个过程倒转过来,在确定未来某一时点上有一定金额的货币,只要 把它看作是那时的本利和,就可按现行利率计算出要能取得这样金额的本利和在现在所必须 具有的本金。 这个逆算出来的本金称为“现值”。现值计算公式是由终值计算公式倒推出 来的 (1 )n S P r = + 4-7
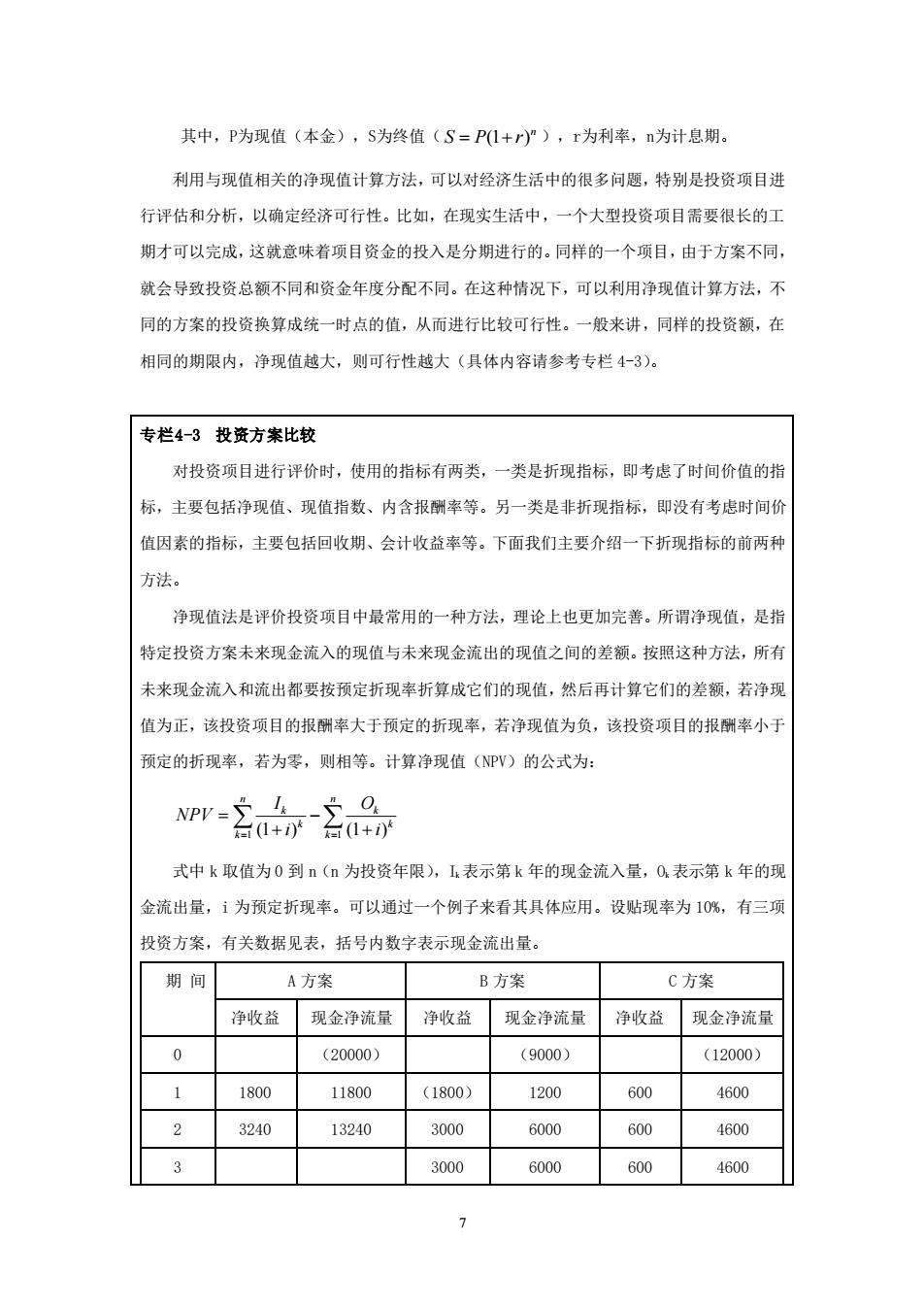
其中,P为现值(本金),S为终值(S=PI+r)”),r为利率,n为计息期。 利用与现值相关的净现值计算方法,可以对经济生活中的很多问题,特别是投资项目进 行评估和分析,以确定经济可行性。比如,在现实生活中,一个大型投资项目需要很长的工 期才可以完成,这就意味着项目资金的投入是分期进行的。同样的一个项目,由于方案不同, 就会导致投资总额不同和资金年度分配不同。在这种情况下,可以利用净现值计算方法,不 同的方案的投资换算成统一时点的值,从而进行比较可行性。一般来讲,同样的投资额,在 相同的期限内,净现值越大,则可行性越大(具体内容请参考专栏4-3)。 专栏4-3投资方案比较 对投资项目进行评价时,使用的指标有两类,一类是折现指标,即考虑了时间价值的指 标,主要包括净现值、现值指数、内含报酬率等。另一类是非折现指标,即没有考虑时间价 值因素的指标,主要包括回收期、会计收益率等。下面我们主要介绍一下折现指标的前两种 方法。 净现值法是评价投资项目中最常用的一种方法,理论上也更加完善。所谓净现值,是指 特定投资方案未来现金流入的现值与未来现金流出的现值之间的差额。按照这种方法,所有 未来现金流入和流出都要按预定折现率折算成它们的现值,然后再计算它们的差额,若净现 值为正,该投资项目的报酬率大于预定的折现率,若净现值为负,该投资项目的报酬率小于 预定的折现率,若为零,则相等。计算净现值(NPV)的公式为: 台(1+)台1+i) 式中k取值为0到n(n为投资年限),Ik表示第k年的现金流入量,O表示第k年的现 金流出量,i为预定折现率。可以通过一个例子来看其具体应用。设贴现率为10%,有三项 投资方案,有关数据见表,括号内数字表示现金流出量。 期间 A方案 B方案 C方案 净收益 现金净流量 净收益 现金净流量 净收益 现金净流量 0 (20000) (9000) (12000) 1 1800 11800 (1800) 1200 600 4600 2 3240 13240 3000 6000 600 4600 3 3000 6000 600 4600
7 其中,P为现值(本金),S为终值( (1 )n S P r = + ),r为利率,n为计息期。 利用与现值相关的净现值计算方法,可以对经济生活中的很多问题,特别是投资项目进 行评估和分析,以确定经济可行性。比如,在现实生活中,一个大型投资项目需要很长的工 期才可以完成,这就意味着项目资金的投入是分期进行的。同样的一个项目,由于方案不同, 就会导致投资总额不同和资金年度分配不同。在这种情况下,可以利用净现值计算方法,不 同的方案的投资换算成统一时点的值,从而进行比较可行性。一般来讲,同样的投资额,在 相同的期限内,净现值越大,则可行性越大(具体内容请参考专栏 4-3)。 专栏4-3 投资方案比较 对投资项目进行评价时,使用的指标有两类,一类是折现指标,即考虑了时间价值的指 标,主要包括净现值、现值指数、内含报酬率等。另一类是非折现指标,即没有考虑时间价 值因素的指标,主要包括回收期、会计收益率等。下面我们主要介绍一下折现指标的前两种 方法。 净现值法是评价投资项目中最常用的一种方法,理论上也更加完善。所谓净现值,是指 特定投资方案未来现金流入的现值与未来现金流出的现值之间的差额。按照这种方法,所有 未来现金流入和流出都要按预定折现率折算成它们的现值,然后再计算它们的差额,若净现 值为正,该投资项目的报酬率大于预定的折现率,若净现值为负,该投资项目的报酬率小于 预定的折现率,若为零,则相等。计算净现值(NPV)的公式为: 1 1 (1 ) (1 ) n n k k k k k k I O NPV i i = = = − + + 式中 k 取值为 0 到 n(n 为投资年限),Ik 表示第 k 年的现金流入量,Ok 表示第 k 年的现 金流出量,i 为预定折现率。可以通过一个例子来看其具体应用。设贴现率为 10%,有三项 投资方案,有关数据见表,括号内数字表示现金流出量。 期 间 A 方案 B 方案 C 方案 净收益 现金净流量 净收益 现金净流量 净收益 现金净流量 0 (20000) (9000) (12000) 1 1800 11800 (1800) 1200 600 4600 2 3240 13240 3000 6000 600 4600 3 3000 6000 600 4600

合计 5040 5040 4200 4200 1800 1800 净现值(A)=(11800/1.1+13240/1.12)-20000=21669-20000=1669(元) 净现值(B)=(1200/1.1+6000/1.1+6000/1.1)-9000=10557-9000=1557(元) 净现值(C)=(4600/1.1+4600/1.12+4600/1.13)-12000=11440-12000=-560(元) A、B两项投资的净现值为正数,说明该方案的报酬率超过10%,则这两个方案是有利的, 从而是可以接受的。C方案的净现值为负数,说明该方案的报酬率达不到10%,所以应该放 弃。A与B相比,A方案更好些。 我们也常使用现值指数作为评价投资方案的指标。所谓现值指数,是未来现金流入现值 与现金流出现值的比率,又称获利指数。其计算公式为: 现值指数=1÷公0 名1+)名1+) 根据上表资料,三个方案的现值指数如下: 现值指数(A)=21669÷20000=1.08 现值指数(B)=10557÷9000=1.17 现值指数(C)=11440÷12000=0.95 A、B两项投资方案的现值指数大于1,说明其收益超过成本,即投资报酬率超过预定折 现率,C项投资方案的现值指数小于1,说明其报酬率没有达到预定折现率。若现值指数为 1,说明折现后现金流入等于流出,投资的报酬率等于预定折现率。其中,B方案现值指数 大于A方案,说明B优于A。 这两种方法中,净现值法是绝对数指标,常用来反映投资效益,而现值指数法则是相对 数指标,用来反映投资的效率。现值指数可以进行独立投资机会获利能力的比较。如果A、B 两方案互斥,根据净现值法,应该选择方案。但如果两者是独立的,人们往往倾向于选择 效率更高的B方案。 (三)衡量利率的指标:到期收益率 在金融市场上存在很多的债务工具,它们的计息方式有很多不同,因而就产生了一个 很现实的问题,有无一个统一的衡量标准来评估这些投资工具的收益率呢?在投资实践中, 人们选择了一个统一的衡量利率高低的工具:到期收益率。到期收益率是使得承诺的未来现 金流量的总现值等于证券当前市场价格的贴现率。到期收益率是衡量利率最准确的指标。下 6
8 合计 5040 5040 4200 4200 1800 1800 净现值(A)=(11800/1.1+13240/1.12)-20000=21669-20000=1669(元) 净现值(B)=(1200/1.1+6000/1.12 +6000/1.13)-9000=10557-9000=1557(元) 净现值(C)=(4600/1.1+4600/1.12 +4600/1.13)-12000=11440-12000=-560(元) A、B 两项投资的净现值为正数,说明该方案的报酬率超过 10%,则这两个方案是有利的, 从而是可以接受的。C 方案的净现值为负数,说明该方案的报酬率达不到 10%,所以应该放 弃。A 与 B 相比,A 方案更好些。 我们也常使用现值指数作为评价投资方案的指标。所谓现值指数,是未来现金流入现值 与现金流出现值的比率,又称获利指数。其计算公式为: 现值指数= 1 1 (1 ) (1 ) n n k k k k k k I O i i = = + + 根据上表资料,三个方案的现值指数如下: 现值指数(A)=21669÷20000=1.08 现值指数(B)=10557÷9000=1.17 现值指数(C)=11440÷12000=0.95 A、B 两项投资方案的现值指数大于 1,说明其收益超过成本,即投资报酬率超过预定折 现率,C 项投资方案的现值指数小于 1,说明其报酬率没有达到预定折现率。若现值指数为 1,说明折现后现金流入等于流出,投资的报酬率等于预定折现率。其中,B 方案现值指数 大于 A 方案,说明 B 优于 A。 这两种方法中,净现值法是绝对数指标,常用来反映投资效益,而现值指数法则是相对 数指标,用来反映投资的效率。现值指数可以进行独立投资机会获利能力的比较。如果A、B 两方案互斥,根据净现值法,应该选择A方案。但如果两者是独立的,人们往往倾向于选择 效率更高的B方案。 (三)衡量利率的指标:到期收益率 在金融市场上存在很多的债务工具,它们的计息方式有很多不同,因而就产生了一个 很现实的问题,有无一个统一的衡量标准来评估这些投资工具的收益率呢?在投资实践中, 人们选择了一个统一的衡量利率高低的工具:到期收益率。到期收益率是使得承诺的未来现 金流量的总现值等于证券当前市场价格的贴现率。到期收益率是衡量利率最准确的指标。下

面我们介绍几种常用的到期收益率。 1.普通贷款到期收益率普通贷款是指资金由贷方贷给借方,双方约定还款的日期和利 息,到期时连本带利一次性偿还。基本公式如下: P=A/1+r) 4-8 P为本金,A为本利和,r为到期收益率,此处等于利率。显然,上式是一年期的普通贷 款的现值计算公式,公式中到期收益率就是贷款利率。如果我们知道了本金和到期的本利总 和,那么我们就可以计算出到期收益率。 2.分期付款的贷款到期收益率这种贷款是由贷方向借方一次性提供一定数额的资金, 双方规定还款期限、每次的还款额度,借方根据合约定期偿还一个固定的数额给贷方,直到 合约结束。基本公式如下: 1+r0+++ P=+4 4-9 (1+r)” 与公式4-8不同的是,这是一个N年期的分期付款贷款,A为不同付款期的本利和,其他 符号相同。一般而言,分期付款贷款在形成贷款合约时,借贷双方对每期的还款金额都很清 楚,那么,根据贷款总额和每期付款的本利和通过现值计算公式就可以推算出到期收益率。 3.息票债券的到期收益率息票债券与其他债券的不同之处,息票债券的利息是由发 行人按照本金和票面利率定时向债券持有人支付,到期时,再将本金连同最后一期利息一起 支付给债券持有人。其计算公式如下: P=C+-C 1+r+炉+.+ C F (0+r1+r) 4-10 其中,r为到期收益率,P为息票债券的市场价格,F为债券到期面值,C是息票的年收 入,n是年限。 4.永久债券的到期收益率永久债券是定期支付利息,而永无到期日的一种债券。其 计算公式如下: Ps、A A A 1+r0+y+0+r+… 4-11 根据无穷递减等比数列的求和公式,上式的右边等于A/r,因此,永久债券的到期收益 率计算公式可以简化: r=A/P 4-12 其中,A为每年末的利息支付额,P为债券市场价格,r为债券到期收益率。 5.折扣债券的到期收益率这种债券在发行时,以面值为基数给买主一个折扣,债券
9 面我们介绍几种常用的到期收益率。 1.普通贷款到期收益率 普通贷款是指资金由贷方贷给借方,双方约定还款的日期和利 息,到期时连本带利一次性偿还。基本公式如下: P A r = + (1 ) 4-8 P为本金,A为本利和,r为到期收益率,此处等于利率。显然,上式是一年期的普通贷 款的现值计算公式,公式中到期收益率就是贷款利率。如果我们知道了本金和到期的本利总 和,那么我们就可以计算出到期收益率。 2.分期付款的贷款到期收益率 这种贷款是由贷方向借方一次性提供一定数额的资金, 双方规定还款期限、每次的还款额度,借方根据合约定期偿还一个固定的数额给贷方,直到 合约结束。基本公式如下: 1 2 2 1 (1 ) (1 ) n n A A A P r r r = + + + + + + 4-9 与公式4-8不同的是,这是一个N年期的分期付款贷款,A为不同付款期的本利和,其他 符号相同。一般而言,分期付款贷款在形成贷款合约时,借贷双方对每期的还款金额都很清 楚,那么,根据贷款总额和每期付款的本利和通过现值计算公式就可以推算出到期收益率。 3.息票债券的到期收益率 息票债券与其他债券的不同之处,息票债券的利息是由发 行人按照本金和票面利率定时向债券持有人支付,到期时,再将本金连同最后一期利息一起 支付给债券持有人。其计算公式如下: 2 1 (1 ) (1 ) (1 ) n n C C C F P r r r r = + + + + + + + + 4-10 其中,r为到期收益率,P为息票债券的市场价格,F为债券到期面值,C是息票的年收 入,n是年限。 4.永久债券的到期收益率 永久债券是定期支付利息,而永无到期日的一种债券。其 计算公式如下: 2 3 1 (1 ) (1 ) A A A P r r r = + + + + + + 4-11 根据无穷递减等比数列的求和公式,上式的右边等于A/r,因此,永久债券的到期收益 率计算公式可以简化: r=A/P 4-12 其中,A为每年末的利息支付额,P为债券市场价格,r为债券到期收益率。 5.折扣债券的到期收益率 这种债券在发行时,以面值为基数给买主一个折扣,债券

持有人在债券到期日,可以从债券发行人那里收回等于面值数量的金额,在持有债券期间, 并无任何名义上的利息。其计算公式如下: P=F/1+r)" 4-13 其中,P为债券的价格,F为面值,r为到期收益率,为期限。 上述多种证券到期收益率的计算,揭示了一个重要定律:当期证券价格与利率负相关。 利率上升,证券价格下降:利率下降,证券价格上升。 到期收益率是衡量利率最精确的指标,一般经济学家所采用的利率概念就是指到期收 益率。由于到期收益率计算比较复杂,有时也会采用衡量利率的近似指标一一当期收益率和 贴现收益率。 二、利息率的相容性 利息率的相容性主要是指存款利率各档次之间的相容问题。贷款利率则一般不存在相容 问题。这是因为存款利率为金融机构吸收资金的手段,对资金供给者而言,利率高低是他决 定供给资金与否的决定因素。在正常情况下,资金供给者会考虑各种利率,特别是会考虑到 复利因素与各种期限的单利的折算关系。因此,银行部门制定存款利率政策,必须充分考虑 复利因素。相容的利率表现为,存款利率的序列的收益规定比较合理,不致出现漏洞或错误, 而导致各种利率之间的政策性矛盾,各种利率相容,则利率杠杆的作用能达到政策上的预期 目的,否则,会产生与政策的预期目的相矛盾的现象。 一般而言,存款利率的相容性具有如下两个原则: 1.在一定时期内,按单利计算方法计算出来的定期存款利息应该大于按复利方法计算出 来的活期存款的利息。假设活期计息期以年为单位,n表示年数:以表示定期利率,以r2 表示活期利率,P为本金,则 P1+r)>P1+5)” 4-14 4-14式的经济意义是国家鼓励定期存款 2.按单利计算的长期定期存款的利息必须大于按复利方法计算出来的期限较短的定期 存款的利息。我们假设表示较长期的定期存款利率,r4表示较短期的定期存款利率,m表 示较长期的定期存款期限,NM表示较短期的定期存款期限,P表示本金,则,上述原则用不 等式表现为: P1+5m)>P(1+r)m 4-15 4-15式的经济意义为国家在支持和鼓励定期存款时更鼓励期限较长的一类。 10
10 持有人在债券到期日,可以从债券发行人那里收回等于面值数量的金额,在持有债券期间, 并无任何名义上的利息。其计算公式如下: (1 )n P F r = + 4-13 其中,P为债券的价格,F为面值,r为到期收益率,n为期限。 上述多种证券到期收益率的计算,揭示了一个重要定律:当期证券价格与利率负相关。 利率上升,证券价格下降;利率下降,证券价格上升。 到期收益率是衡量利率最精确的指标,一般经济学家所采用的利率概念就是指到期收 益率。由于到期收益率计算比较复杂,有时也会采用衡量利率的近似指标——当期收益率和 贴现收益率。 二、利息率的相容性 利息率的相容性主要是指存款利率各档次之间的相容问题。贷款利率则一般不存在相容 问题。这是因为存款利率为金融机构吸收资金的手段,对资金供给者而言,利率高低是他决 定供给资金与否的决定因素。在正常情况下,资金供给者会考虑各种利率,特别是会考虑到 复利因素与各种期限的单利的折算关系。因此,银行部门制定存款利率政策,必须充分考虑 复利因素。相容的利率表现为,存款利率的序列的收益规定比较合理,不致出现漏洞或错误, 而导致各种利率之间的政策性矛盾,各种利率相容,则利率杠杆的作用能达到政策上的预期 目的,否则,会产生与政策的预期目的相矛盾的现象。 一般而言,存款利率的相容性具有如下两个原则: 1.在一定时期内,按单利计算方法计算出来的定期存款利息应该大于按复利方法计算出 来的活期存款的利息。假设活期计息期以年为单位,n表示年数;以r1表示定期利率,以r2 表示活期利率,P为本金,则 1 2 (1 ) (1 )n P r P r + + 4-14 4-14式的经济意义是国家鼓励定期存款。 2.按单利计算的长期定期存款的利息必须大于按复利方法计算出来的期限较短的定期 存款的利息。我们假设r3表示较长期的定期存款利率,r4表示较短期的定期存款利率,m表 示较长期的定期存款期限,N/M表示较短期的定期存款期限,P表示本金,则,上述原则用不 等式表现为: 3 4 (1 ) (1 )m P r m P r + + 4-15 4-15式的经济意义为国家在支持和鼓励定期存款时更鼓励期限较长的一类