
回归这个统计术语,最早采用者是英国遗传学家高尔登。他把这种统计分析方法应用于 研究生物学的遗传问题,指出生物后代有回复或回归到其上代原有特性的倾向。高尔登的学 主皮尔逊继续研 ,将回归的 数学的方法联系起来,把代表现象之间一般数量关系的 直线或曲线称为回归直线或回归曲线。 相关分析中的相关系数可以从数量上说明变量之间相关关系的方向和密切程度。但它不 能反映一个变量发生一定数量的变化时.另一个变量会相应的发生多少变动。为了解决这个 问题,就必须采用回归分析的方法。回归分析是指对具有相关关系的变量,依据其关系形态 选择一个合适的数学模型,用来近似的表示变量之间数量平均变化关系的一种统计方法。回 归分析的内容很多,按分析变量的多少不同,可分为一元回归分析和多元回归分析:按分析 变量的表现形态不同,可分为线性回归分析与非线性回归分析等。本节只讨论一元线性回归 分析的理论与方法。 10.3.1一元线性回归模型的描述 元线性回归模型也称为简单直线回归模型,是分析两个变量x与y之间相互关系的数 学方程式。我们假定x为自变量,y为因变量,y值除了受自变量x的影响之外,还受其它 因素的影响:在构建回归模型时,应该包括随机误差£,x与y之间的关系可以用数学公 式表示: y=a+bx+g (10-3) 在实际研究问题时,为了便于对参数做出区间估计和假设检验,我们假定~N(0,σ)· 因此,我们可以用下式近似的描述x与y之间的关系: j=a+bx (10-4) 式中y为因变量的估计值:x为自变量的实际值:a,b为待定参数:公式(10-4)称 为变量y对x的一元线性回归模型。 a,b的几何意义是:a为直线方程的截距,b为直线的斜率。其经济意义是:a表示自 变量x为零时的因变量y的估计值:b表示当自变量x每增加一个单位时因变量y的平均变 化,b也称为y对x的回归系数。 10.3.2一元线性回归方程的拟合 元线性回归方程的建立,是对两个变量进行回归分析的第一步,下面我们不妨以某企 业广告费支出与销售额之间的关系问题为例来进行说明。资料如表10-4所示 我们可以在平面直角坐标系上画出广告费支出与销售额的散点图。见图10-2。 表10-4某企业广告费支出与销售额数据(单位:万元) 广告费x 67 4 5 39 销售额y 50587040603037 80
6 回归这个统计术语,最早采用者是英国遗传学家高尔登。他把这种统计分析方法应用于 研究生物学的遗传问题,指出生物后代有回复或回归到其上代原有特性的倾向。高尔登的学 生皮尔逊继续研究,将回归的概念和数学的方法联系起来,把代表现象之间一般数量关系的 直线或曲线称为回归直线或回归曲线。 相关分析中的相关系数可以从数量上说明变量之间相关关系的方向和密切程度。 但它不 能反映一个变量发生一定数量的变化时. 另一个变量会相应的发生多少变动。为了解决这个 问题, 就必须采用回归分析的方法。 回归分析是指对具有相关关系的变量, 依据其关系形态, 选择一个合适的数学模型,用来近似的表示变量之间数量平均变化关系的一种统计方法。回 归分析的内容很多,按分析变量的多少不同,可分为一元回归分析和多元回归分析;按分析 变量的表现形态不同, 可分为线性回归分析与非线性回归分析等。 本节只讨论一元线性回归 分析的理论与方法。 10.3.1 一元线性回归模型的描述 一元线性回归模型也称为简单直线回归模型, 是分析两个变量 x 与 y 之间相互关系的数 学方程式。我们假定 x 为自变量,y 为因变量,y 值除了受自变量 x 的影响之外,还受其它 因素的影响;在构建回归模型时,应该包括随机误差e ,x 与 y 之间的关系可以用数学公 式表示: y = a + bx + e (10-3) 在实际研究问题时, 为了便于对参数做出区间估计和假设检验, 我们假定 2 e ~ N(0,s ) 。 因此,我们可以用下式近似的描述 x 与 y 之间的关系: yˆ = a + b x (10-4) 式中 y ˆ 为因变量的估计值;x 为自变量的实际值;a ,b 为待定参数;公式(10-4)称 为变量 y 对 x 的一元线性回归模型。 a ,b 的几何意义是:a 为直线方程的截距,b 为直线的斜率。其经济意义是:a 表示自 变量 x 为零时的因变量 y 的估计值;b 表示当自变量 x 每增加一个单位时因变量 y 的平均变 化,b 也称为 y 对 x 的回归系数。 10.3.2 一元线性回归方程的拟合 一元线性回归方程的建立,是对两个变量进行回归分析的第一步, 下面我们不妨以某企 业广告费支出与销售额之间的关系问题为例来进行说明。资料如表 10-4 所示: 我们可以在平面直角坐标系上画出广告费支出与销售额的散点图。见图 10-2 。 表 10-4 某企业广告费支出与销售额数据(单位:万元) 广告费 x 6 7 8 4 5 2 3 9 销售额 y 50 58 70 40 60 30 37 80
8000 70.00 0 60.00 50.00 40.00 0 0 30.000 2.00 3.00 4.00 5.00 6.00 7.008009.00 图10-2某企业广告费支出与销售额散点图 从散点图,我们可以看到,大体上销售额y是随者广告费的增加而增加,大致成一条直 线,可以认为y与x满足一元线性回归模型(10-4)。那么,现在的问题是,如何找到一条 直线=+bx,使这条直线尽可能的靠近所有的样本点呢?我们可以利用最小二乘法 做到这一点。 最小二乘法的基本思想是:选择a和b,使得观测值y与理论值少的离差平方和最 小。即选择a和b,使得 Q=∑y-)=最小值 (10-5) 用直线方程少=a+bx代入公式得: Q=∑0y-)》2=∑(y-a-bx)2=最小值 (10-6) 用数学中对二元函数求极值的原理,计算Q关于a和b的偏导数,并令其等于零,即 >
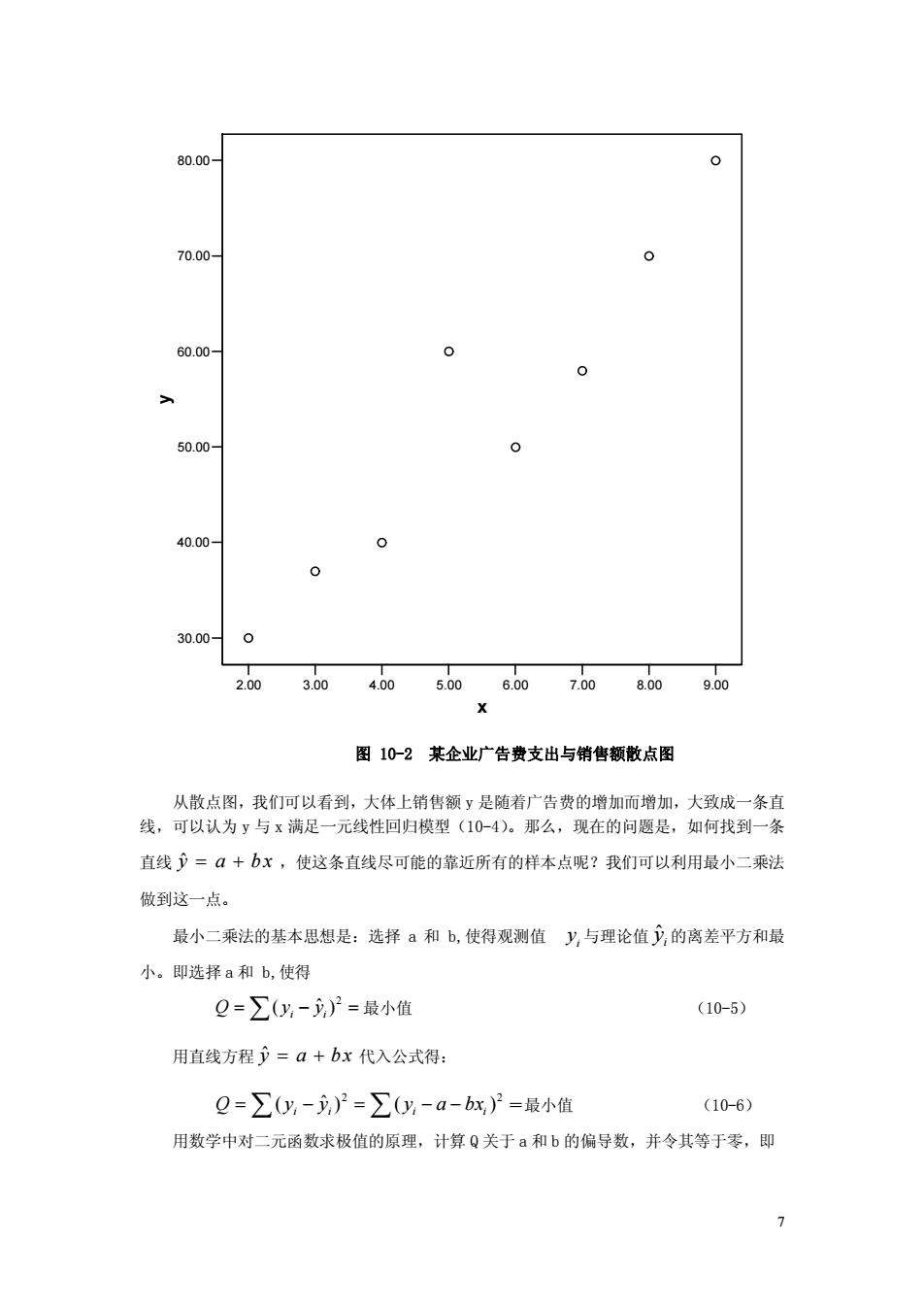
7 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 x 30.00 40.00 50.00 60.00 70.00 80.00 y 图 10-2 某企业广告费支出与销售额散点图 从散点图,我们可以看到,大体上销售额 y 是随着广告费的增加而增加,大致成一条直 线,可以认为 y 与 x 满足一元线性回归模型(10-4) 。那么,现在的问题是,如何找到一条 直线 yˆ = a + b x ,使这条直线尽可能的靠近所有的样本点呢?我们可以利用最小二乘法 做到这一点。 最小二乘法的基本思想是:选择 a 和 b,使得观测值 i y 与理论值 ˆ i y 的离差平方和最 小。即选择 a 和 b,使得 2 ( ˆ ) Q i i = Â y - y = 最小值 (10-5) 用直线方程 yˆ = a + bx 代入公式得: 2 2 ( ˆ ) ( ) Q i i i i = Â y - y = Â y - a - bx =最小值 (10-6) 用数学中对二元函数求极值的原理,计算 Q 关于 a 和 b 的偏导数,并令其等于零,即