
海南大学教案 课程名称:电工技术 任课教师: 第2章电路的分析方法 计划学时:8学时 教学目的和要求: 1.掌握等效变换法、支路电流法、叠加原理和戴维宁定理等电路的 基本分析方法: 2.了解实际电源的两种模型及其等效变换: 3.了解受控源、非线性电阻元件的伏安特性及静态电阻、动态电阻 的概念,以及简单非线性电阻电路的图解分析法。 重点: 等效变换法、支路电流法、叠加原理和戴维宁定理 难点: 戴维宁定理 作业思考题: 作业:2.1.1,2.1.8,2.3.3,2.3.4,2.4.2,2.5.3,2.6.1,2.6.2, 2.7.2,2.7.5,2.7.8 思考:2.1.2,2.1.3,2.1.6,2.1.7,2.3.1,2.3.2,2.7.9,2.7.11 17
17 海南大学教案 课程名称:电工技术 任课教师: 第 2 章 电路的分析方法 计划学时:8 学时 教学目的和要求: 1. 掌握等效变换法、支路电流法、叠加原理和戴维宁定理等电路的 基本分析方法; 2. 了解实际电源的两种模型及其等效变换; 3. 了解受控源、非线性电阻元件的伏安特性及静态电阻、动态电阻 的概念,以及简单非线性电阻电路的图解分析法。 重点: 等效变换法、支路电流法、叠加原理和戴维宁定理 难点: 戴维宁定理 作业思考题: 作业:2.1.1,2.1.8,2.3.3,2.3.4,2.4.2,2.5.3,2.6.1,2.6.2, 2.7.2,2.7.5,2.7.8 思考:2.1.2,2.1.3,2.1.6,2.1.7,2.3.1,2.3.2,2.7.9,2.7.11

第2章电路的分析方法 $2.1电阻串并联联接的等效变换 一.电阻的串联 各电阻一个接一个地顺序相联,通过 同一电流,称为电阻的串联。串联电阻的 0 等效电阻等于各电阻之和,串联电阻上电 压的分配与电阻成正比。 右图所示两个电阻的等效电阻为: R=R+R2 R 两电阻串联时的分压公式: 4=RR" =风吊R0 其应用:降压、限流、调节电压等 二.电阻的并联 联接在两个公共的结点之间的各电阻 称为并联。其特点为各电阻两端的电压相同: +112 等效电阻的倒数等于各电阻倒数之和:各电 阻电流的大小与电阻成反比。 右图所示等效电阳为:食名记 两电阻并联时的分流公式: 其应用:分流、调节电流等。 18
18 第2章 电路的分析方法 §2.1 电阻串并联联接的等效变换 一. 电阻的串联 各电阻一个接一个地顺序相联,通过 同一电流,称为电阻的串联。串联电阻的 等效电阻等于各电阻之和,串联电阻上电 压的分配与电阻成正比。 右图所示两个电阻的等效电阻为: R =R1+R2 两电阻串联时的分压公式: U R R R U 1 2 1 1 U R R R U 1 2 2 2 其应用:降压、限流、调节电压等。 二. 电阻的并联 联接在两个公共的结点之间的各电阻 称为并联。其特点为各电阻两端的电压相同; 等效电阻的倒数等于各电阻倒数之和;各电 阻电流的大小与电阻成反比。 右图所示等效电阻为: 1 2 1 1 1 R R R 两电阻并联时的分流公式: I R R R I 1 2 2 1 I R R R I 1 2 1 2 其应用:分流、调节电流等
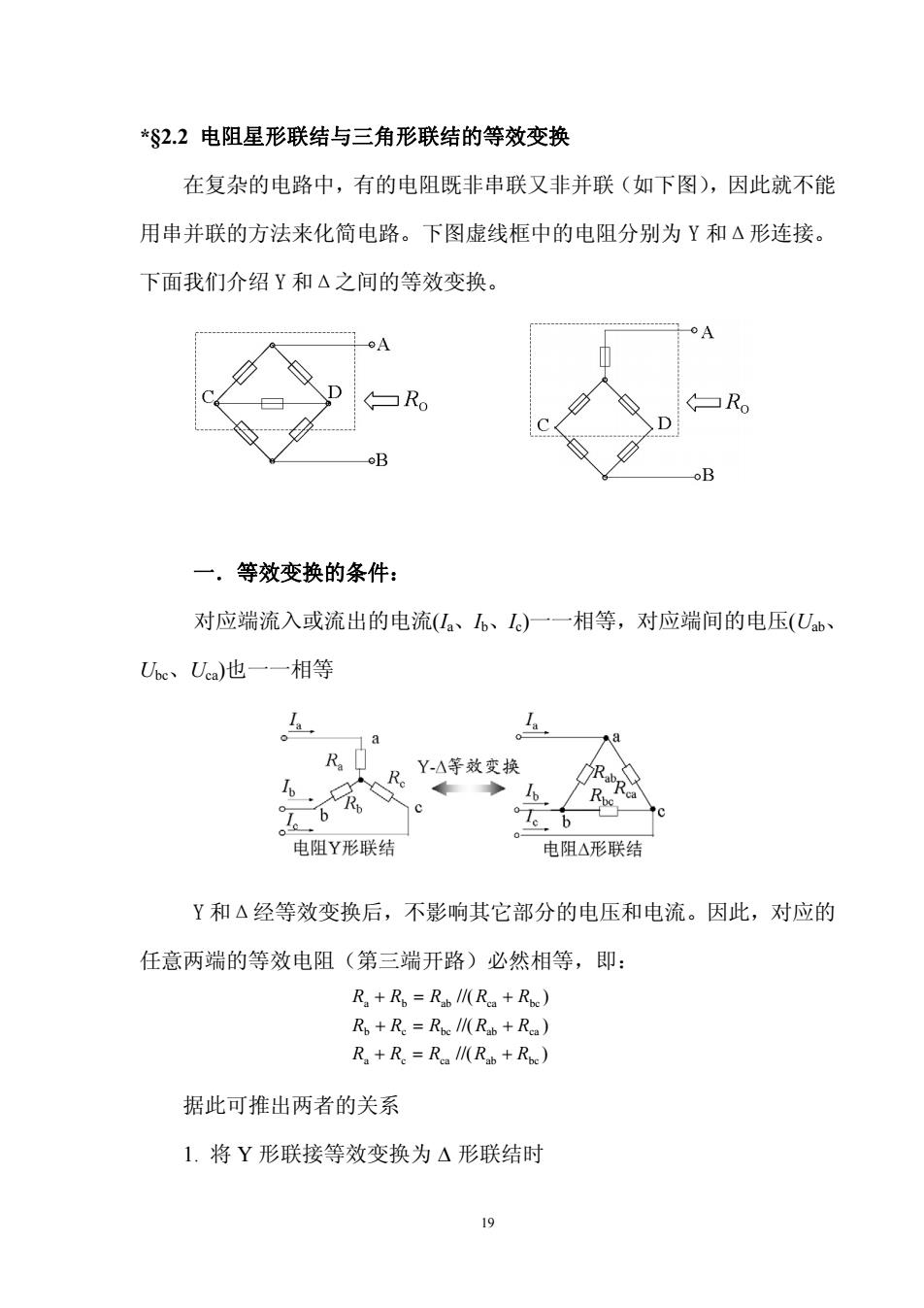
*S2.2电阻星形联结与三角形联结的等效变换 在复杂的电路中,有的电阻既非串联又非并联(如下图),因此就不能 用串并联的方法来化简电路。下图虚线框中的电阻分别为Y和△形连接。 下面我们介绍Y和△之间的等效变换。 □R R。 D 一。等效变换的条件: 对应端流入或流出的电流(Ia、)一一相等,对应端间的电压(Ub、 Ue、Uca)也一一相等 Y-△等效变换 ←◆ e b 电阻Y形联结 电阻△形联结 Y和△经等效变换后,不影响其它部分的电压和电流。因此,对应的 任意两端的等效电阻(第三端开路)必然相等,即: R,+R=R l(R+R) Rs+Re=Rpe ll(Rg +R) R,+Re=R l(Rsb Re) 据此可推出两者的关系 1.将Y形联接等效变换为△形联结时 19
19 *§2.2 电阻星形联结与三角形联结的等效变换 在复杂的电路中,有的电阻既非串联又非并联(如下图),因此就不能 用串并联的方法来化简电路。下图虚线框中的电阻分别为 Y 和Δ形连接。 下面我们介绍 Y 和Δ之间的等效变换。 一.等效变换的条件: 对应端流入或流出的电流(Ia、Ib、Ic)一一相等,对应端间的电压(Uab、 Ubc、Uca)也一一相等 Y 和Δ经等效变换后,不影响其它部分的电压和电流。因此,对应的 任意两端的等效电阻(第三端开路)必然相等,即: 据此可推出两者的关系 1. 将 Y 形联接等效变换为 形联结时 //( ) //( ) //( ) a c ca ab bc b c bc ab ca a b ab ca bc R R R R R R R R R R R R R R R

R。=RR+RR+RR R R-kR+RR+RR R R-BR+RR+RR 若Ra=Ro=Re=Ry时,有Rab=Rc=RaFR=3RY 2.将△形联接等效变换为Y形联结时 RRca R.-RstRx+Ra Rhe Rab R.=BatRx+R R Rie R.-Rat RetRo 若Rab=Re=Rca=R△,有Ra=Rb=Re=RY=RW3 例1:对图示电路求总电阻R2 1- 22 022 0.89 19 D R12◆ 0.49 0.42 22 /18 2 200 1 12 2 10.82 1 ☐2.6842 12 21 例2:计算下图电路中的电流I
20 若 Ra=Rb=Rc=RY 时,有 Rab=Rbc=Rca= R = 3RY 2. 将 形联接等效变换为 Y 形联结时 若 Rab=Rbc=Rca= R ,有 Ra=Rb=Rc=RY =R/3 例 1:对图示电路求总电阻 R12 例 2:计算下图电路中的电流 I1 b a b b c c a ca a a b b c c a bc c a b b c c ab R R R R R R R R R R R R R R R R R R R R R R R R a ab bc ca ca bc c ab bc ca bc ab b ab bc ca ab ca a R R R R R R R R R R R R R R R R R R
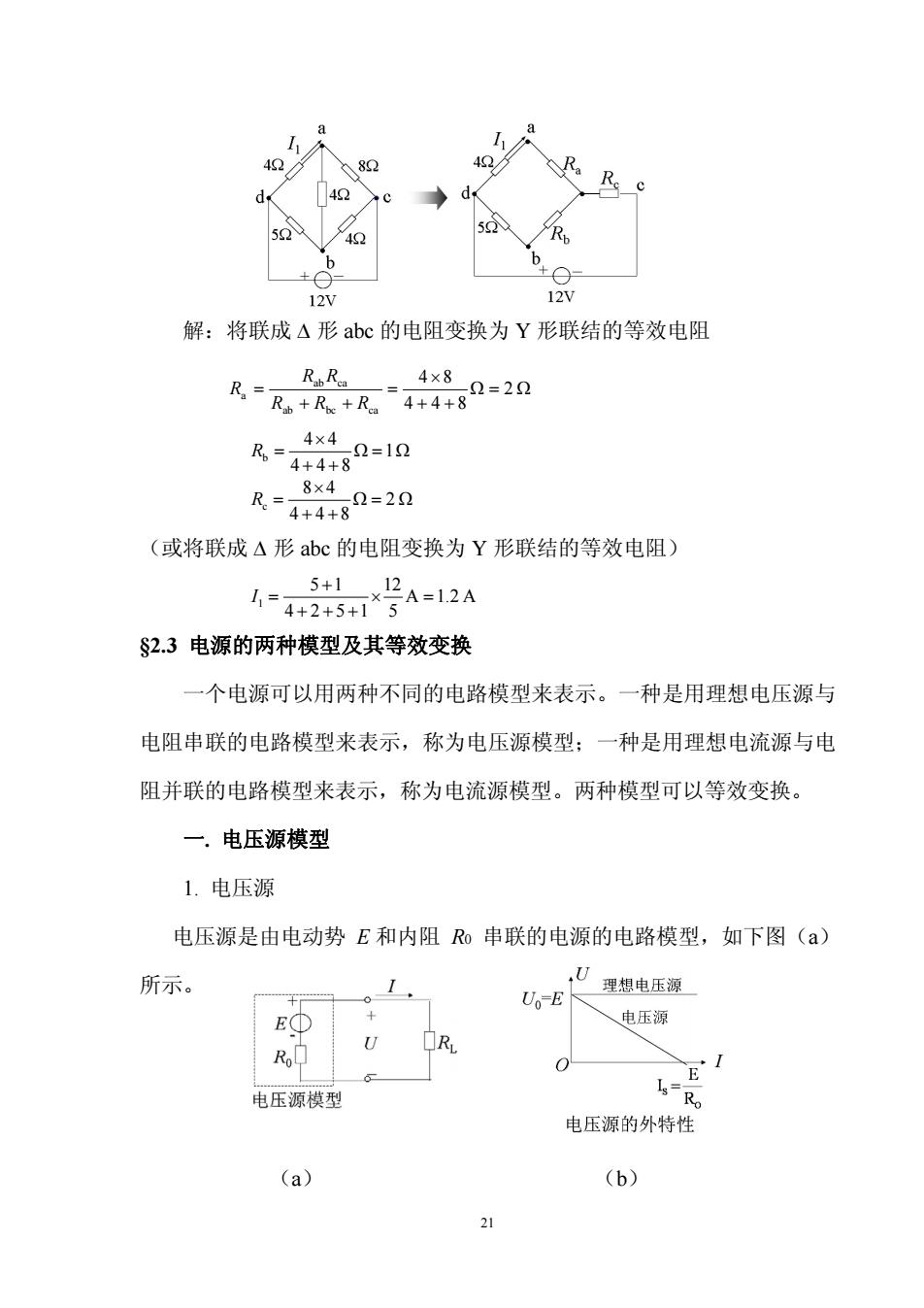
12 12V 解:将联成△形abc的电阻变换为Y形联结的等效电阻 RR 4×8 RR+R+R4+4+80=20 4×4 R-4480=1n R=7460=2n (或将联成△形abc的电阻变换为Y形联结的等效电阻) 5+1 2A-12A 1=4+2+5+1 $2.3电源的两种模型及其等效变换 一个电源可以用两种不同的电路模型来表示。一种是用理想电压源与 电阻串联的电路模型来表示,称为电压源模型:一种是用理想电流源与电 阻并联的电路模型来表示,称为电流源模型。两种模型可以等效变换。 一.电压源模型 1.电压源 电压源是由电动势E和内阻Ro串联的电源的电路模型,如下图(a) 所示。 0 U。E 理想电压源 E① 、电压源 R 电压源模型 R 电压源的外特性 (a) (b) 21
21 解:将联成 形 abc 的电阻变换为 Y 形联结的等效电阻 Ω 2 Ω 4 4 8 4 8 ab bc ca ab ca a R R R R R R Ω 1Ω 4 4 8 4 4 b R Ω 2 Ω 4 4 8 8 4 c R (或将联成 形 abc 的电阻变换为 Y 形联结的等效电阻) A 1.2 A 5 12 4 2 5 1 5 1 1 I §2.3 电源的两种模型及其等效变换 一个电源可以用两种不同的电路模型来表示。一种是用理想电压源与 电阻串联的电路模型来表示,称为电压源模型;一种是用理想电流源与电 阻并联的电路模型来表示,称为电流源模型。两种模型可以等效变换。 一. 电压源模型 1. 电压源 电压源是由电动势 E 和内阻 R0 串联的电源的电路模型,如下图(a) 所示。 (a) (b)