
如将NHCI(s)放入含有HCI(g)和NH(g)体系 中分解,则因×HCIg≠×NH3g 所以R'=0,C=3-1-0=2 请大家将书P253中内容认真仔细看几遍。 (3)在上述推导中,我们曾假定每一个相中都 含有$种物质。可以证明,如果某一相中不含 有某种物质,相律的形式不变。 F=C-P+2
16 如将NH4Cl(s)放入含有HCl(g)和NH3 (g)体系 中分解,则因xHCl(g) xNH3(g) 所以R = 0,C = 3 – 1 – 0 = 2 请大家将书P253中内容认真仔细看几遍。 (3) 在上述推导中,我们曾假定每一个相中都 含有S种物质。可以证明,如果某一相中不含 有某种物质,相律的形式不变。 F = C – P + 2

(④)相律是根据热力学平衡条件推导而来, 所以相律只适用于平衡条件时F、C、P的计 算。对非平衡态不适用。 (5)相律中数字“2”是由于假定外界条件只有 温度和压力可以影响体系的平衡状态而来的 (通常情况下确是如此)。如体系恒定T或P(即 T或P一确定值),则相律可写作 F*=C-P+1 如体系T和P都确定,则相律为 F**=C-P F*、F*统称为“条件自由度
17 (4) 相律是根据热力学平衡条件推导而来, 所以相律只适用于平衡条件时F、C、P的计 算。对非平衡态不适用。 (5) 相律中数字“2”是由于假定外界条件只有 温度和压力可以影响体系的平衡状态而来的 (通常情况下确是如此)。如体系恒定T或P(即 T或P一确定值),则相律可写作: F* = C – P + 1 如体系T和P都确定,则相律为 F** = C – P F*、 F**统称为“条件自由度”

在有些体系中,除T、p外,还考虑到 其它因素(如磁场、电池、重力场等)的影响, 此时可用“n”代替为“2”,n是能够影响体 系平衡状态的外界因素的个数,则相律一般 的形式为:F=C-P+n 5.相律的意义 借助于相律可以确定研究复杂的多组分 体系的方向,确定相平衡体系中独立变量的 函数关系
18 在有些体系中,除T、p外,还考虑到 其它因素(如磁场、电池、重力场等)的影响, 此时可用“n”代替为“2”,n是能够影响体 系平衡状态的外界因素的个数,则相律一般 的形式为:F = C – P + n 5. 相律的意义 借助于相律可以确定研究复杂的多组分 体系的方向,确定相平衡体系中独立变量的 函数关系

§6.2 杠杆规则 1.杠杆规则推导 依据:物质守恒定律 n总XM nL×L ncXG (原来溶液中A ,(分配在液相中 (分配在气相中 的总物质的量)A的物质的量) A的物质的量) 因为 n总 n液+n气 (n液+n)XM=nX+ncXG nL(XM-X1)=nG(XG-XM)
19 n总xM = nL xL + nG xG (原来溶液中A (分配在液相中 (分配在气相中 的总物质的量) A的物质的量) A的物质的量) 因为 n总 = n液 + n气 (n液 + n气) xM = nL xL + nG xG nL (xM-x1 ) = nG (xG -xM) §6.2 杠杆规则 1. 杠杆规则推导 依据: 物质守恒定律
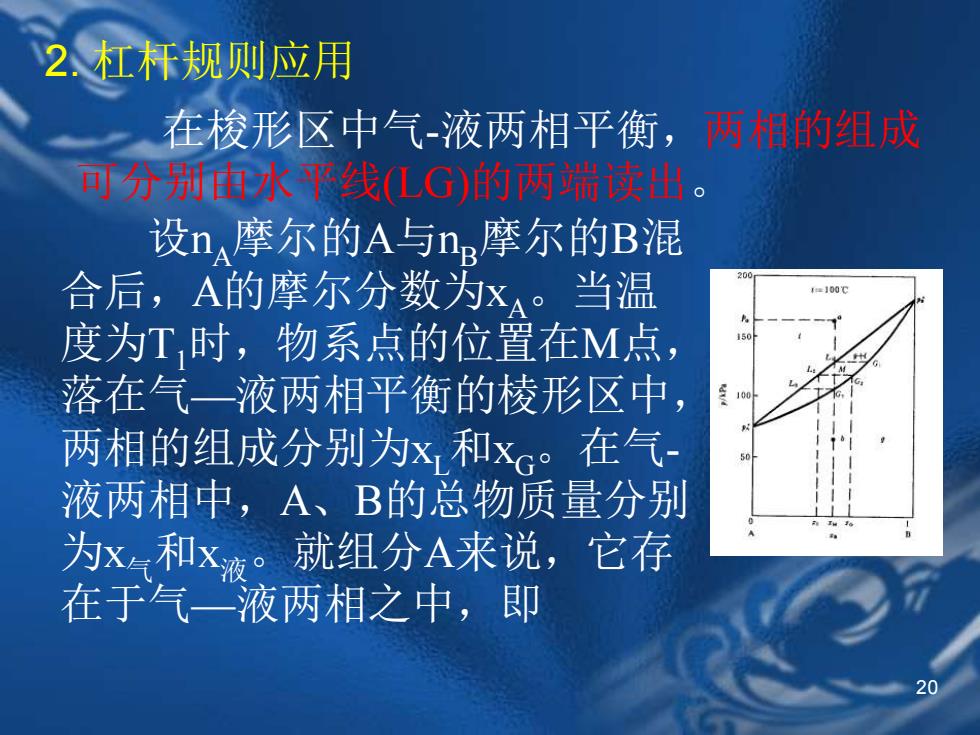
2杠杆规则应用 在梭形区中气-液两相平衡,两相的组成 可分别由水平线(LG)的两端读出。 设n摩尔的A与n.摩尔的B混 合后,A的摩尔分数为x。当温 =100C 度为T时,物系点的位置在M点, 落在气一液两相平衡的棱形区中, 两相的组成分别为x和x。在气- 液两相中,A、B的总物质量分别 为x气和x液。就组分A来说,它存 在于气一液两相之中,即
20 2. 杠杆规则应用 设nA摩尔的A与nB摩尔的B混 合后,A的摩尔分数为xA。当温 度为T1时,物系点的位置在M点, 落在气—液两相平衡的棱形区中, 两相的组成分别为xL和xG。在气- 液两相中,A、B的总物质量分别 为x气和x液。就组分A来说,它存 在于气—液两相之中,即 在梭形区中气-液两相平衡,两相的组成 可分别由水平线(LG)的两端读出