《电磁场理论》课程电子教案（讲义）第一章 矢量分析

dS.=e.dl,dl,=e.dxdy 体积元： dV=dxdyd= 2.圆柱坐标系 =8,(圆面 二=0（平面） 球山 P(ro.Bo.do) P=Po (圆柱面) 中=4 一（半平面 (半平面) 球坐标系 圆柱坐标 坐标变量 坐标单位矢量 epese: 位置矢量 F=ep+e= 线元失量 di-edp+epdo+e.d正 d5。=edl,dl.=e.pdd d。=e,dldl.=e,dpd 面元矢量 ds.=e.dldl。=e.pdpd 体积元 dV=pdpdd 3.球坐标系 d -de

S e l l e x y d z zd xd y zd d    = = 体积元 ： dV = dxdydz 2. 圆柱坐标系 坐标变量 ,,z 坐标单位矢量 z e e e    , ,   位置矢量 r e e zz    =  + 线元矢量 l e e e z d d d zd     =   +   + 面元矢量               = = = = = =                 d d d d d d d d d d d d d d d z z z z z S e l l e S e l l e z S e l l e z          体积元 dV = dddz 3. 球坐标系 圆柱坐标 系  =0 （半平面）  = 0 （圆柱面） z = z0 （平面） ( , , ) 0 0 0 P   z 圆柱坐标系中的线元、面元和体积元 球坐标系 球坐标系中的线元、面元和体积元

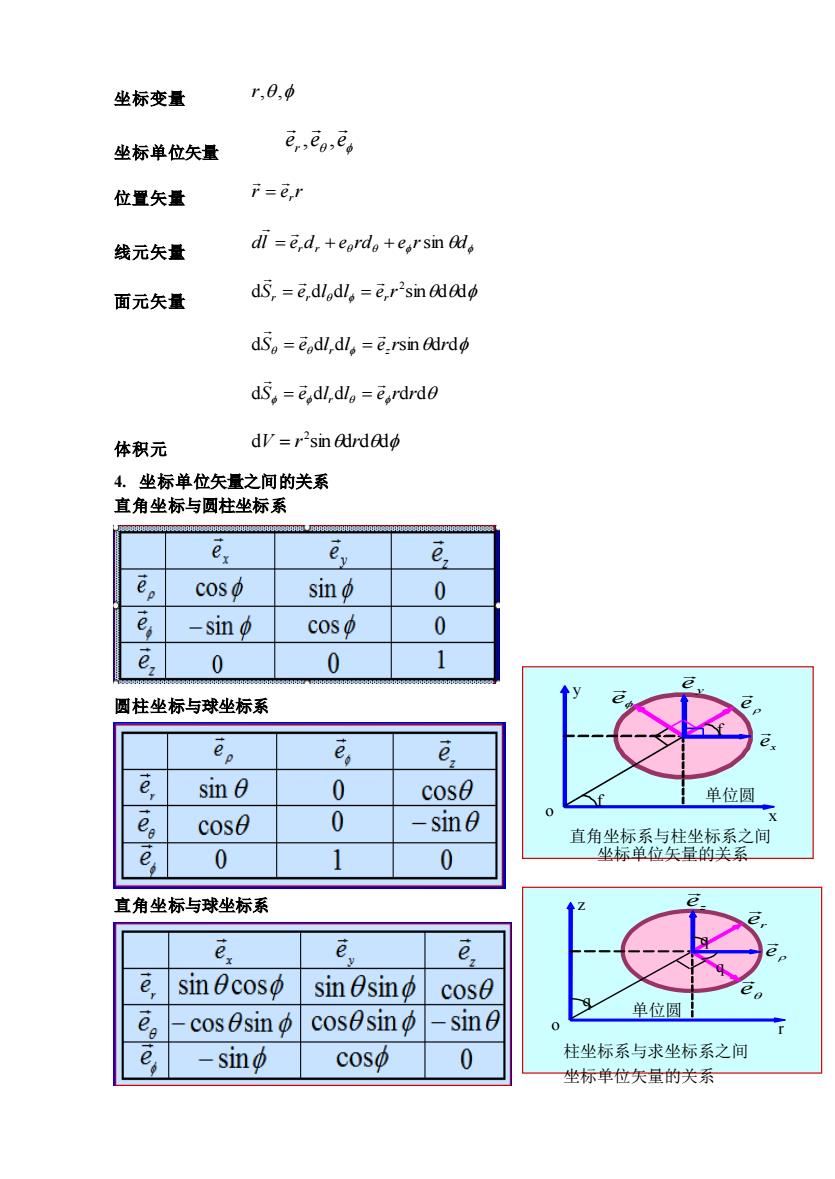
坐标变量 r.0.0 坐标单位矢量 e,eoses 位置失量 F=er 线元矢量 dl =ed,+eordo+ersin ad, 面元矢量 dS,=e,dld山，=e,r2sin69 dS。=ed,d。=e.rsin dS。=e,dl,d。-e,rdrd0 体积元 dy=r"sin ardao 4.坐标单位矢量之间的关系 直角坐标与圆柱坐标系 e e g cos sin 0 e -sin coso 0 e: 0 0 圆柱坐标与球坐标系 e sin 0 0 cose 单位圆 cos0 0 -sin e, 0 1 0 直角坐标与球坐标系 e.sin0coso sinθsin cose 单位圆} e。 cosesin cosesin-sine -sino coso 0 柱坐标系与求坐标系之间 坐标单位关量的关系

坐标变量 r,, 坐标单位矢量   e e e r    , , 位置矢量 r e rr   = 线元矢量    d dl e d e rd e r r r = + + sin   面元矢量 d d d  sindd 2 S e l l e r r r r    = = dS edl rdl  ez rsindrd    = = dS edl rdl  e rdrd    = = 体积元 d sind dd 2 V = r r 4. 坐标单位矢量之间的关系 直角坐标与圆柱坐标系 圆柱坐标与球坐标系 直角坐标与球坐标系 o f x y 单位圆 直角坐标系与柱坐标系之间 坐标单位矢量的关系 f e x  e y  e   e  o q r z 单位圆 柱坐标系与求坐标系之间 坐标单位矢量的关系 q q e z  e   e r  e 