3、光学仪器的分辨率 满足瑞利判据的两物点间的距离,就是光学仪器所能分辨的最 小距离。对透镜中心所张的角0称为最小分辨角。0=1.22入/D 最小分辨角的倒数称为 仪器的分辨本领 L D 0.612 1.222 讨论: •分辨本领与D成正比,与波长成 反比:D大,分辨本领大;波长小, 分辨本领大 圆孔衍射公式对抛物面式的天线, 雷达均成立
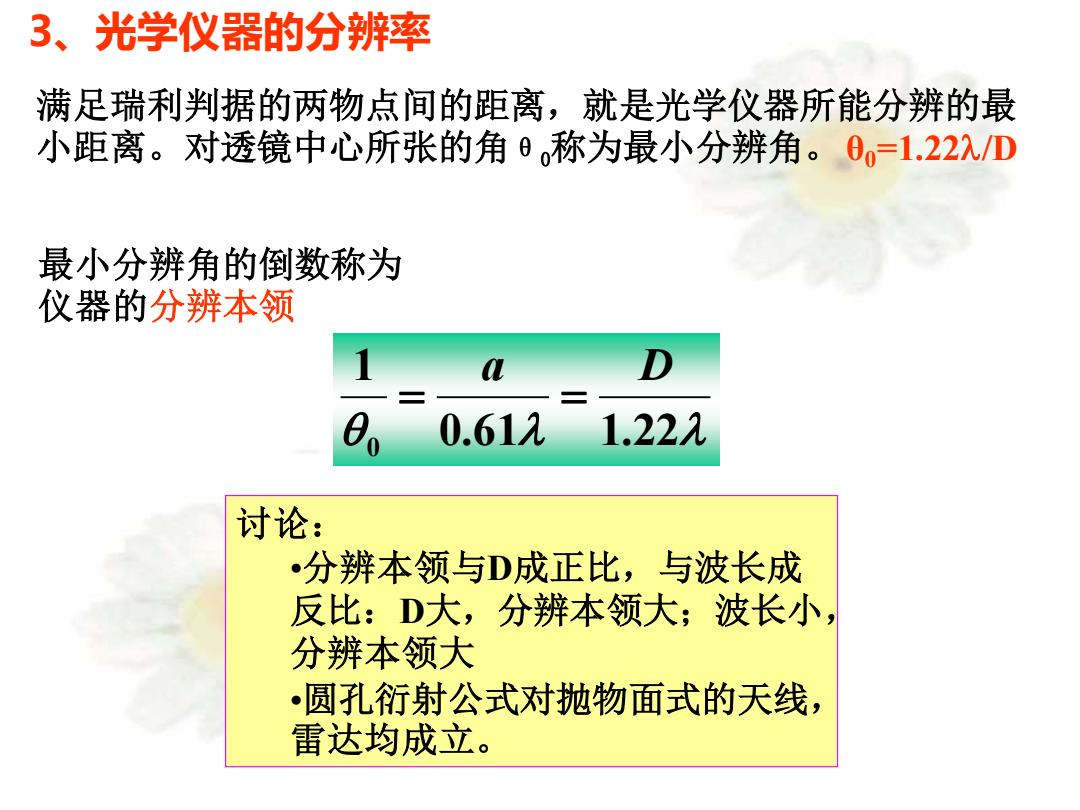
满足瑞利判据的两物点间的距离,就是光学仪器所能分辨的最 小距离。对透镜中心所张的角θ0称为最小分辨角。θ0=1.22/D 最小分辨角的倒数称为 仪器的分辨本领 3、光学仪器的分辨率 0.61 1.22 1 0 a D = = 讨论: •分辨本领与D成正比,与波长成 反比:D大,分辨本领大;波长小, 分辨本领大 •圆孔衍射公式对抛物面式的天线, 雷达均成立

Figure 13.18 The highly reflecting metal foil that covers the Hubble space telescope minimizes the temperature changes that would otherwise occur during each orbit around the earth. Figure This image of the ionized ga (yellow)at the heart of galaxy M87 was ob tained by the Hubble space telescope.The circle identifies the center of the galaxy.at Figure The Hubble space telescope. which a black hole is thought to exist
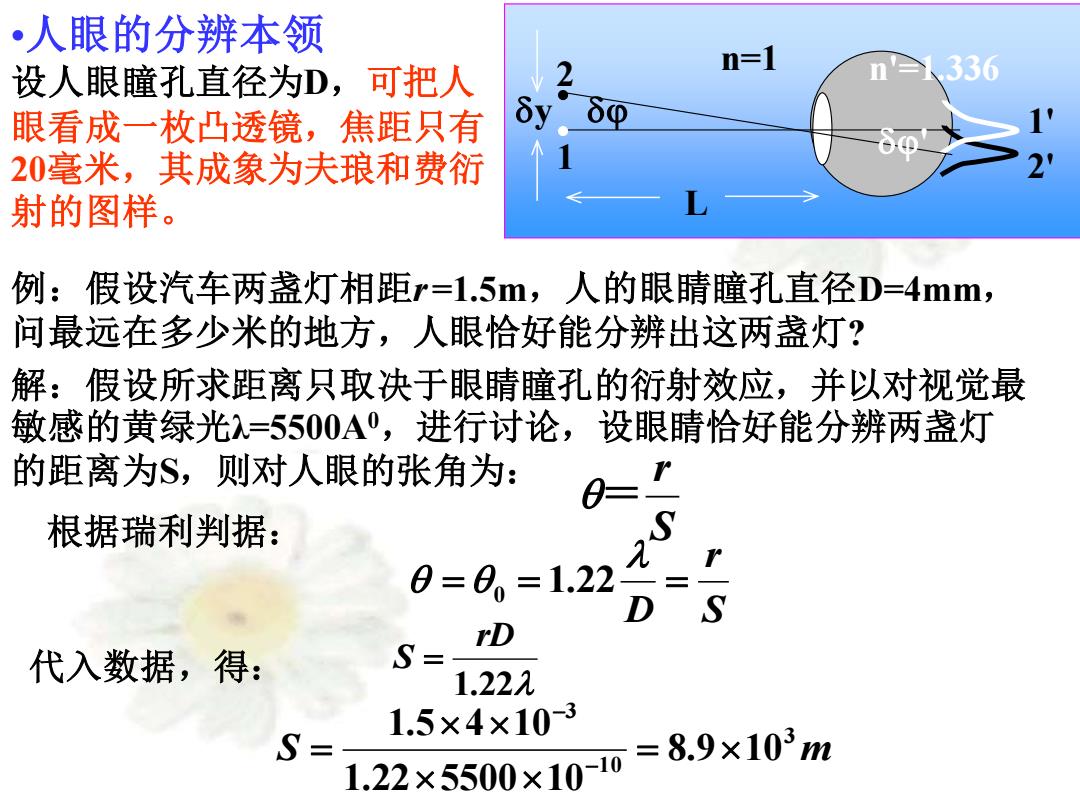
•人眼的分辨本领 设人眼瞳孔直径为D,可把人 n=1 n'336 眼看成一枚凸透镜,焦距只有 8y 20毫米,其成象为夫琅和费衍 射的图样。 例:假设汽车两盏灯相距r=1.5m,人的眼晴瞳孔直径D=4mm, 问最远在多少米的地方,人眼恰好能分辨出这两盏灯? 解:假设所求距离只取决于眼睛瞳孔的衍射效应,并以对视觉最 敏感的黄绿光=5500A·,进行讨论,设眼晴恰好能分辨两盏灯 的距离为S,则对人眼的张角为: 0=1 根据瑞利判据: 0=0。=1.22 S= D 代入数据,得: 1.22元 1.5×4×10-3 S= 1.22×5500×100=8.9×103m
例:假设汽车两盏灯相距r =1.5m,人的眼睛瞳孔直径D=4mm, 问最远在多少米的地方,人眼恰好能分辨出这两盏灯? 解:假设所求距离只取决于眼睛瞳孔的衍射效应,并以对视觉最 敏感的黄绿光λ=5500A0,进行讨论,设眼睛恰好能分辨两盏灯 的距离为S,则对人眼的张角为: S r = 根据瑞利判据: S r D = = = 0 1.22 1.22 rD 代入数据,得: S = S m 3 1 0 3 8.9 10 1.22 5500 10 1.5 4 10 = = − − •人眼的分辨本领 设人眼瞳孔直径为D,可把人 眼看成一枚凸透镜,焦距只有 20毫米,其成象为夫琅和费衍 射的图样。 y n=1 n'=1.336 ' L 1 2 1' 2

§17-9 衍射光栅 引言:对于单缝: 若缝宽大,条纹亮,但条纹间距小,不易分辨 若缝宽小,条纹间距大,但条纹暗,也不易分辨 因而利用单缝衍射不能精确地进行测量。 问题:能否得到亮度大,分得开,宽度窄的明条纹? 结论:利用衍射光栅所形成的衍射图样一光栅光谱 应用: 精确地测量光的波长; 是重要的光学元件,广泛应用于物理,化学,天文, 地质等基础学科和近代生产技术的许多部门
§17-9 衍射光栅 引言:对于单缝: 若缝宽大,条纹亮,但条纹间距小,不易分辨 若缝宽小,条纹间距大,但条纹暗,也不易分辨 因而利用单缝衍射不能精确地进行测量。 问题:能否得到亮度大,分得开,宽度窄的明条纹? 结论:利用衍射光栅所形成的衍射图样——光栅光谱 应用: 精确地测量光的波长; 是重要的光学元件,广泛应用于物理,化学,天文, 地质等基础学科和近代生产技术的许多部门