1-1质点运动的描述 TA=xAi+yaj 2 Tg=xgi+ygj yB B- yA _YB-YA 位移△产=B一下4 =(xg-x4)i+(0yB-yA)万 XBX 若质点在三维空间中运动 XB-XA △F=(xB-xA)i+(yB-yA)万j+(3B-2A)k 位移的大小为 △F=V△2+△y2+△z2 4路程(△S)质点实际运动轨迹的长度
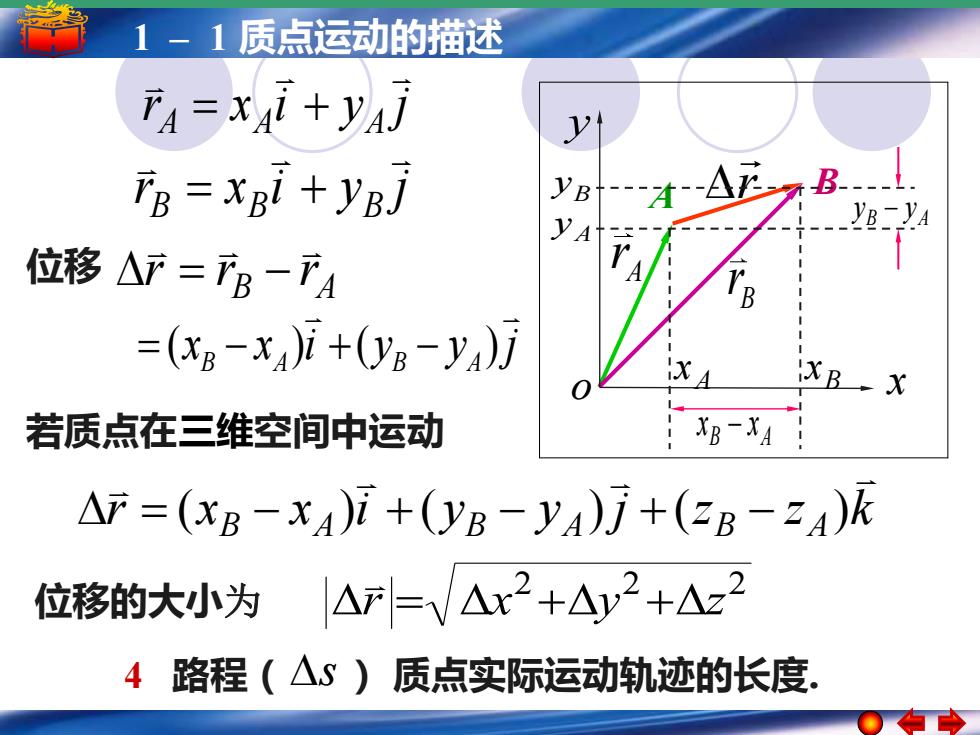
5 –1 1 –简谐运动 1 质点运动的描述 简谐运动的振幅 周期 频率和相位 2 2 2 r = x +y +z 位移的大小为 A r B B r A r x y o B x A x B A x − x B y A y B A y − y r x i y j A A A = + r x i y j B B B = + x x i y y j B A B A = ( − ) +( − ) B A r r r 位移 = − 若质点在三维空间中运动 r x x i y y j z z k B A B A B A = ( − ) + ( − ) + ( − ) 4 路程(s ) 质点实际运动轨迹的长度
1-1质点运动的描述 位移的物理意义 1 A.S 1)反映物体在空间位置 的变化,与路径无关,只决定 于质点的始末位置, 2)反映了运动的矢量 性和叠加性。 △产=△xi+△yi+△zk ∫P(x,2) △F=V△2+△y2+△c2 LP2(x2,y2,22) 三注意 A产≠△r 位矢长度的变化 △=yx+y,+-x2+y+
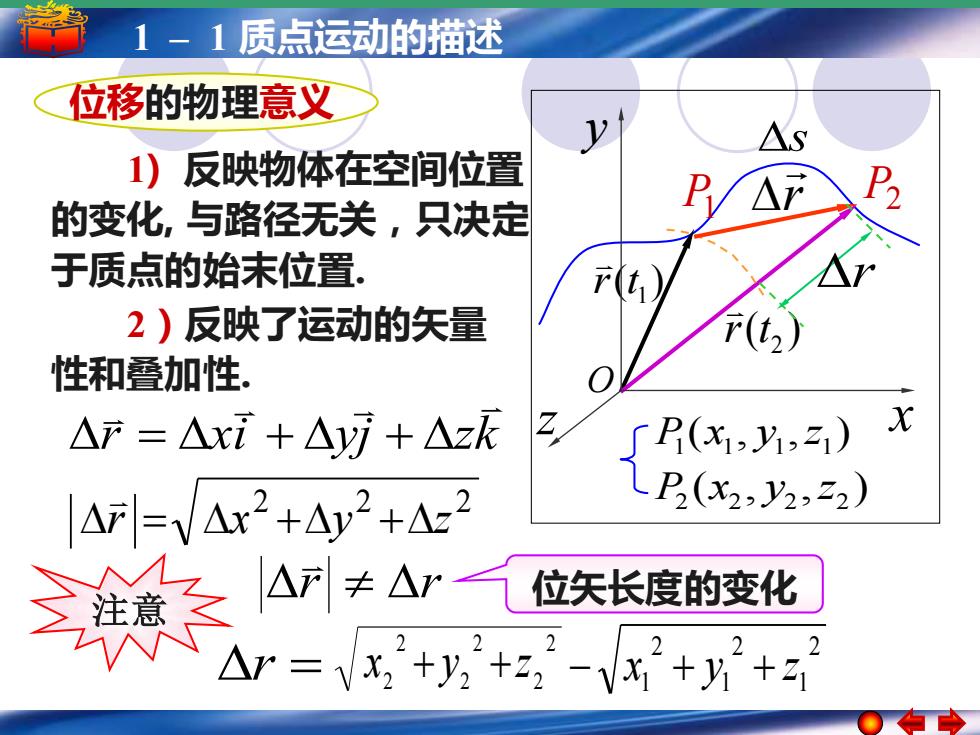
5 –1 1 –简谐运动 1 质点运动的描述 简谐运动的振幅 周期 频率和相位 2 2 2 r = x +y +z r r 2 1 2 1 2 1 − x + y + z 2 2 2 2 2 2 r = x + y +z 位移的物理意义 1) 反映物体在空间位置 的变化, 与路径无关,只决定 于质点的始末位置. 2)反映了运动的矢量 性和叠加性. s ( , , ) 1 1 1 1 P x y z ( , , ) 2 2 2 2 P x y z ( ) 1 r t P1 ( ) 2 r t r P2 注意 x y O z r r xi yj zk = + + 位矢长度的变化