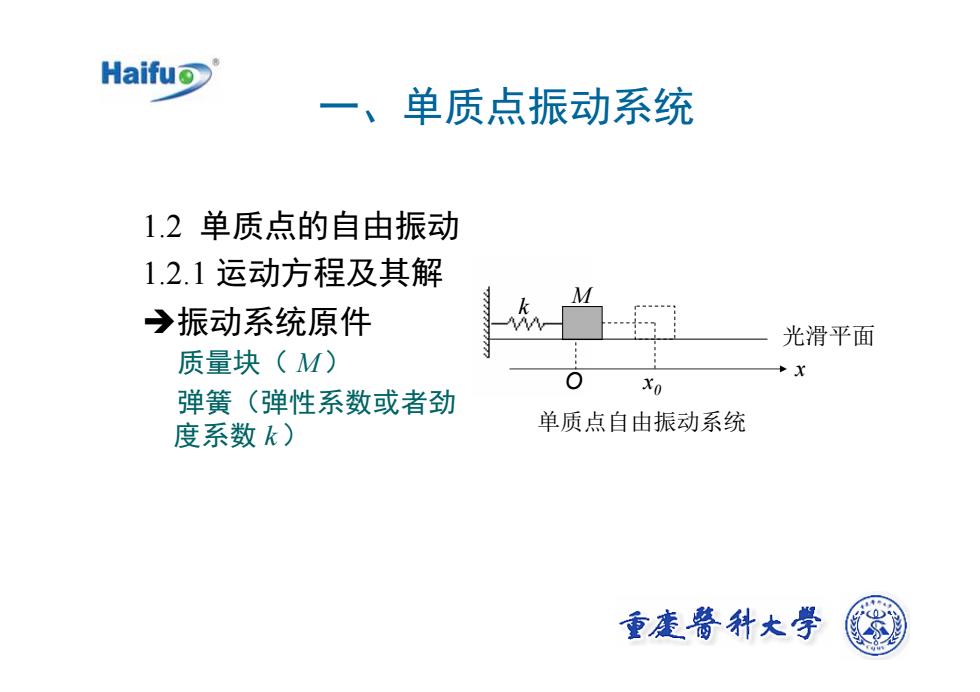
Haifuo一、单质点振动系统1.2单质点的自由振动1.2.1运动方程及其解M>振动系统原件光滑平面质量块(M)+x0Xo弹簧(弹性系数或者劲单质点自由振动系统度系数k)重广醫科大学
一、单质点振动系统 1.2 单质点的自由振动 1.2.1 运动方程及其解 Î振动系统原件 质量块( M ) 弹簧(弹性系数或者劲 度系数 k ) k M O x 0 x 光滑平面 单质点自由振动系统
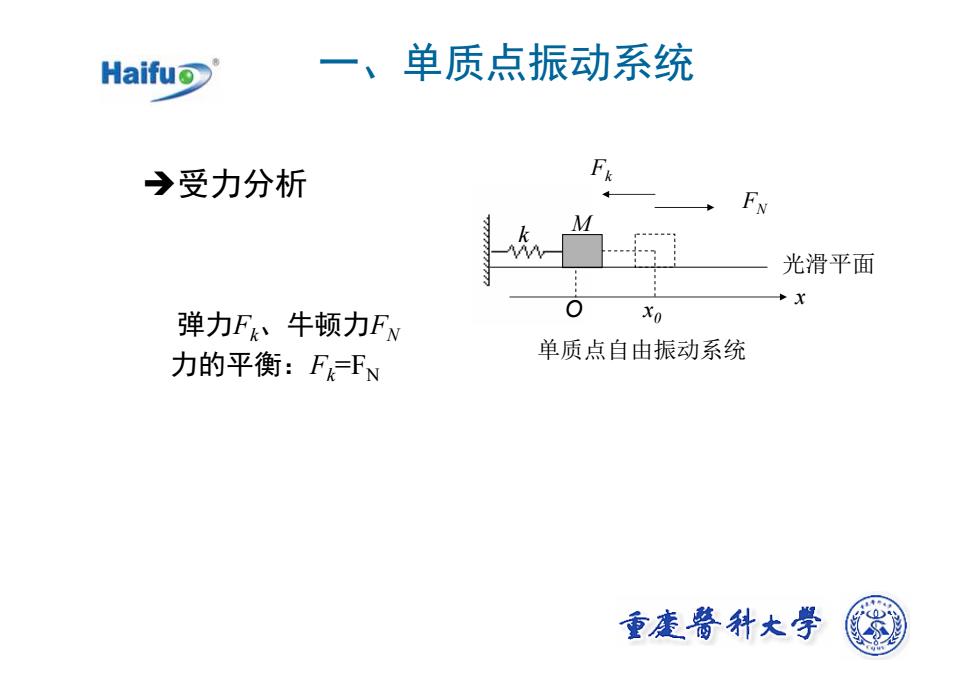
一、单质点振动系统HaifuFk>受力分析FNMV光滑平面+x0Xo弹力F、牛顿力FN单质点自由振动系统力的平衡:Fk=Fn重广科大学
一、单质点振动系统 Î受力分析 弹力 Fk、牛顿力 FN 力的平衡: Fk=F N k M O x 0 x 光滑平面 单质点自由振动系统 FN Fk
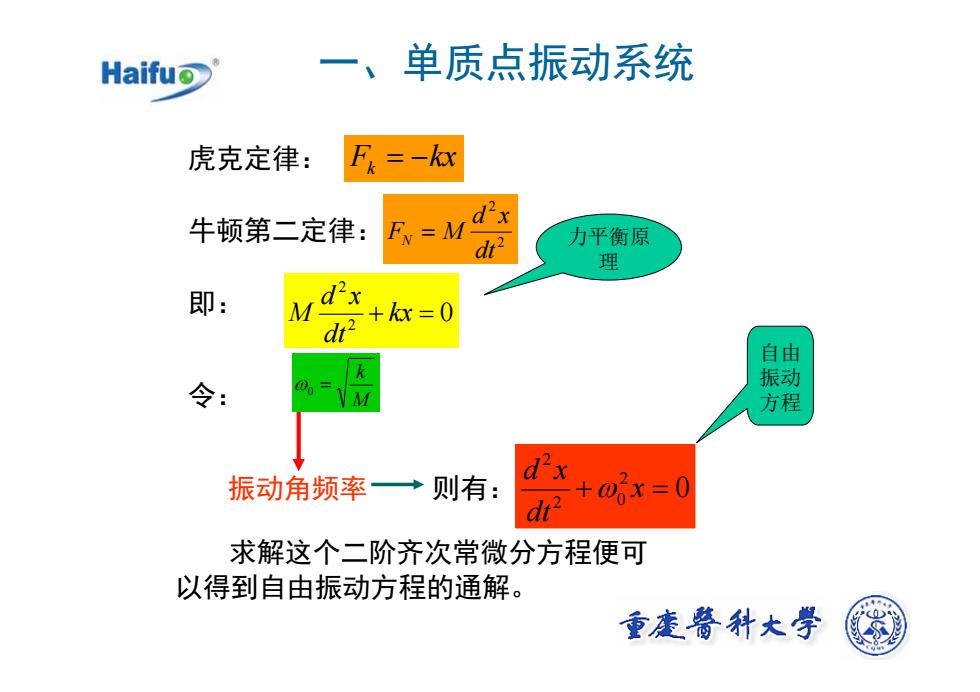
一、单质点振动系统HaifuF=-kx虎克定律:Fi=Md'x牛顿第二定律:力平衡原dt?理d'x即:M+ kx=0dt自由K振动00=VM令:方程d'x+0x=0→则有:振动角频率dt?求解这个二阶齐次常微分方程便可以得到自由振动方程的通解。重广醫科大学
M k ω0 = 一、单质点振动系统 F kx k = − 2 2 dt d x FN = M 0 2 2 + kx = dt d x M 虎克定律: 牛顿第二定律: 即: 力平衡原 理 令: 振动角频率 则有: 自由 振动 方程 求解这个二阶齐次常微分方程便可 以得到自由振动方程的通解。 0 2 2 0 2 + x = dt d x ω
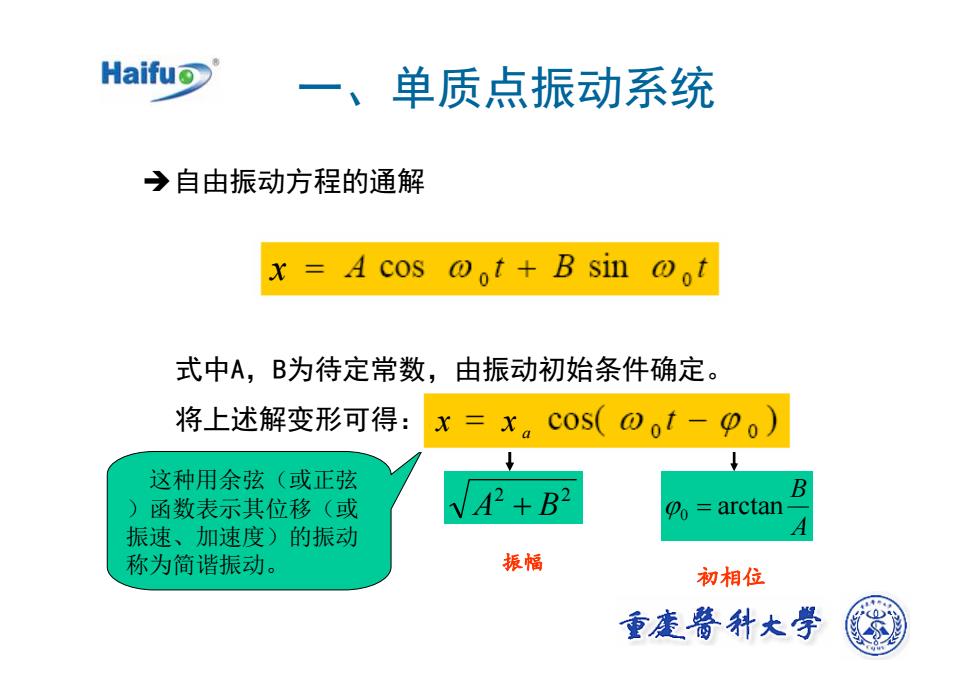
Haifu一、单质点振动系统>自由振动方程的通解x=Acoso。t+Bsinot式中A,B为待定常数,由振动初始条件确定将上述解变形可得:x =x. cos( @ot - P。)这种用余弦(或正弦BVA+B2函数表示其位移(或Po=arctanA振速、加速度)的振动振幅称为简谐振动。初相位重广醫科大学
一、单质点振动系统 Î自由振动方程的通解 2 2 A + B 式中A,B为待定常数,由振动初始条件确定。 将上述解变形可得: 初相位 A B arctan ϕ0 = 振幅 这种用余弦(或正弦 )函数表示其位移(或 振速、加速度)的振动 称为简谐振动。 x x x a