
§4.1恒定磁场的基本规律 二、比奥-萨伐尔定律 由实验得到: 线电流:B= 其中R=下-下, 面电流:B= 州 B称为磁感应强度 4元 R 单位为:T(特斯拉) 你电流R=公 Wb/m2(韦伯/平方米) 4π
§4.1恒定磁场的基本规律 二、比奥-萨伐尔定律 ' 0 3 ' 0 3 0 ' 3 4 4 4 l S S V Idl R B R J dS R B R J R B dV R 由实验得到 线 : : : 电流 面电流 体电流: ' 2 , / / R r r B T Wb m 其中 称为磁感应强度 单位为:(特斯拉) (韦伯 平方米)

§4.1恒定磁场的基本规律 讨论与引伸 1)适用条件:无限大均匀煤质(4),且电流分布 在有限区域内。 2)由毕奥一沙伐定律可以导出恒定滋场的基本方 程(B的散度与旋度)。 例题参见书上P113页例1一例3
§4.1恒定磁场的基本规律 2)由毕奥—沙伐定律可以导出恒定磁场的基本方 程( 的散度与旋度)。 1)适用条件:无限大均匀媒质 ,且电流分布 在有限区域内。 ( ) B 例题参见书上P113页例1-例3

§4.1恒定磁场的基本规律 三、磁感应强度的远区特性 当电流分布在有限空间, 且观察点趋向于无穷远(→0)时 B= R=r-r wax+o1
§4.1恒定磁场的基本规律 三、磁感应强度的远区特性 0 ' ' ' 3 3 3 3 0 ' ' 3 3 ( ) 4 1 ( ) 1 [{ ( ) } ( )] 4 V V r R B J r dV R r r R R r O R r r r B J r dV O r r 当电流分布在有限空间, 且观察点趋向于无穷远( )时
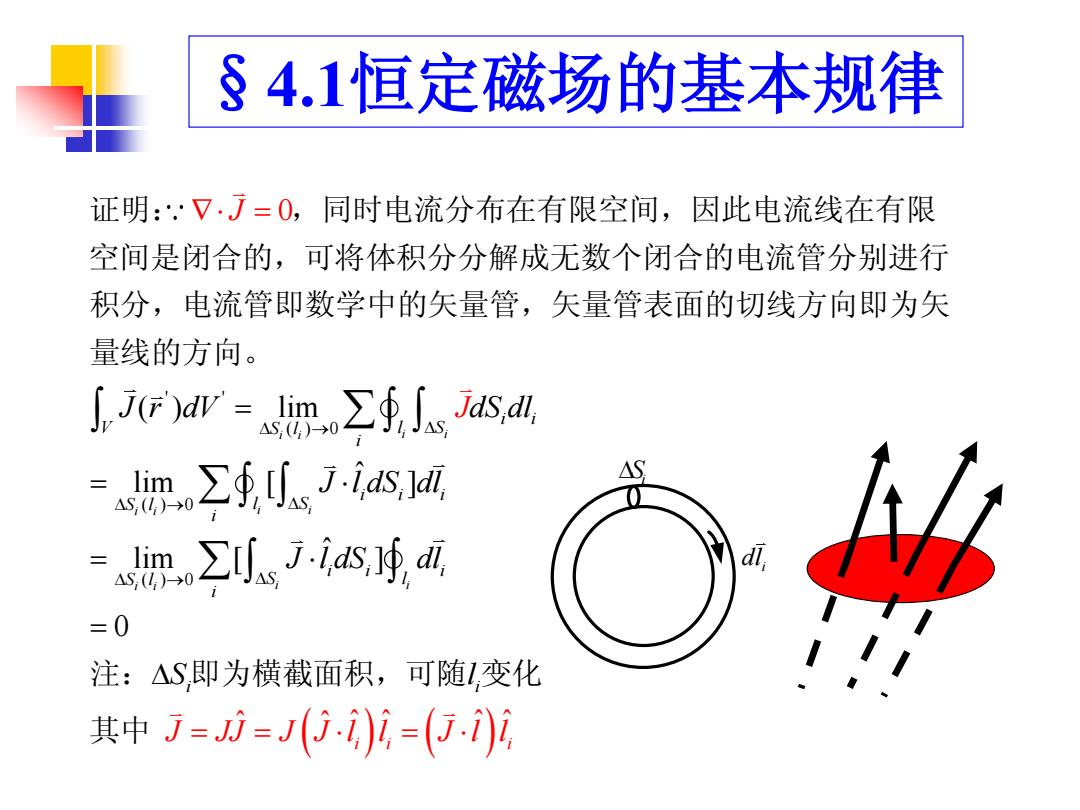
§4.1恒定磁场的基本规律 证明:.V·J=0,同时电流分布在有限空间,因此电流线在有限 空间是闭合的,可将体积分分解成无数个闭合的电流管分别进行 积分,电流管即数学中的矢量管,矢量管表面的切线方向即为矢 量线的方向。 ∫JFar=km∑∮,∫ssaM =m∑∮./-ias1a △S =m∑7.ids,fl dl, =0 注:△S,即为横截面积,可随1,变化 其中j=方=j)1=(5.)1
§4.1恒定磁场的基本规律 ' ' ( ) 0 ( ) 0 ( ) 0 ( ) lim ˆ lim [ ] ˆ lim [ ] 0 i i i i i i i i i i i i V l S S l i i i i S l l S i i i S l S J r d J V dS dl J J l dS dl J l dS 证明: ,同时电流分布在有限空间,因此电流线在有限 空间是闭合的,可将体积分分解成无数个闭合的电流管分别进行 积分,电流管即数学中的矢量管,矢量管表面的切线方向即为矢 量线的方向。 ˆ ˆ ˆ ˆ ˆ ˆ 0 i i i i i i i i i l dl S l J JJ J J l l J l l 注: 即为横截面积,可随 变化 其中 i S i dl

§4.1恒定磁场的基本规律 所以磁感应强度的零级近似为0(即忽略尺寸) 物理意义:没有磁荷或者说没有通量源(与静电场类比) 由于零级近似为零,所以无限远处比E小一个数量级 可表示为B=0 磁信极你产牛的场+0习
§4.1恒定磁场的基本规律 3 3 4 1 1 1 B 0 B B O r B O O r r B E 所以磁感应强度 的零级近似为(即忽略尺寸) 没有磁荷或者说没有通量源(与静电场类比) 由于零级近似 磁偶极距产 为零,所以无限远处 比 小一个数量级 可表示 物理意义: 为 生的场+