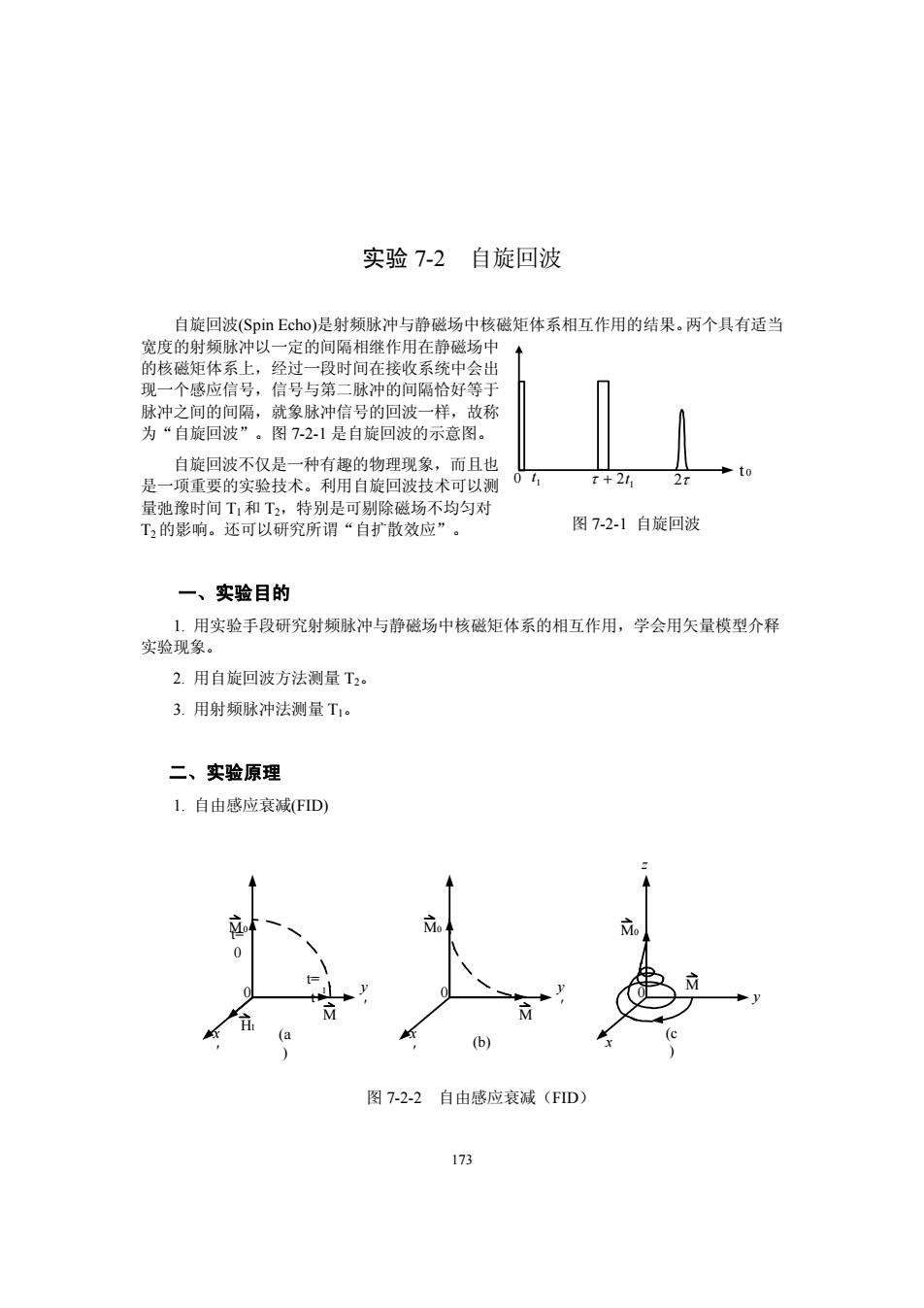
实验7-2自旋回波 自旋回波(Spin Echo)是射频脉冲与静磁场中核磁矩体系相互作用的结果。两个具有适当 宽度的射频脉冲以一定的间隔相继作用在静磁场中 的核磁矩体系上,经过一段时间在接收系统中会出 现一个感应信号,信号与第二脉冲的间隔恰好等于 脉冲之间的间隔,就象脉冲信号的回波一样,故称 为“自旋回波”。图7-2-1是自旋回波的示意图。 自旋回波不仅是一种有趣的物理现象,而且也 是一项重要的实验技术。利用自旋回波技术可以测 01 T+21 量弛豫时间T1和T2,特别是可剔除磁场不均匀对 T2的影响。还可以研究所谓“自扩散效应”。 图7-2-1自旋回波 一、实验目的 1.用实验手段研究射频脉冲与静磁场中核磁矩体系的相互作用,学会用矢量模型介释 实验现象。 2.用自旋回波方法测量T2。 3.用射频脉冲法测量T1。 二、实验原理 1.自由感应衰减FD) 2 M 0 (b) (c 图7-2-2自由感应衰减(FID) 173
173 实验 7-2 自旋回波 自旋回波(Spin Echo)是射频脉冲与静磁场中核磁矩体系相互作用的结果。两个具有适当 宽度的射频脉冲以一定的间隔相继作用在静磁场中 的核磁矩体系上,经过一段时间在接收系统中会出 现一个感应信号,信号与第二脉冲的间隔恰好等于 脉冲之间的间隔,就象脉冲信号的回波一样,故称 为“自旋回波”。图 7-2-1 是自旋回波的示意图。 自旋回波不仅是一种有趣的物理现象,而且也 是一项重要的实验技术。利用自旋回波技术可以测 量弛豫时间 T1 和 T2,特别是可剔除磁场不均匀对 T2 的影响。还可以研究所谓“自扩散效应”。 一、实验目的 1. 用实验手段研究射频脉冲与静磁场中核磁矩体系的相互作用,学会用矢量模型介释 实验现象。 2. 用自旋回波方法测量 T2。 3. 用射频脉冲法测量 T1。 二、实验原理 1. 自由感应衰减(FID) t 0 0 t1 τ + 2t1 2τ 图 7-2-1 自旋回波 y ' x ' 0 t= t 1 t= 0 y ' x ' 0 z y x 0 M0 M0 M M0 M M H1 (a ) (b) (c ) 图 7-2-2 自由感应衰减(FID)
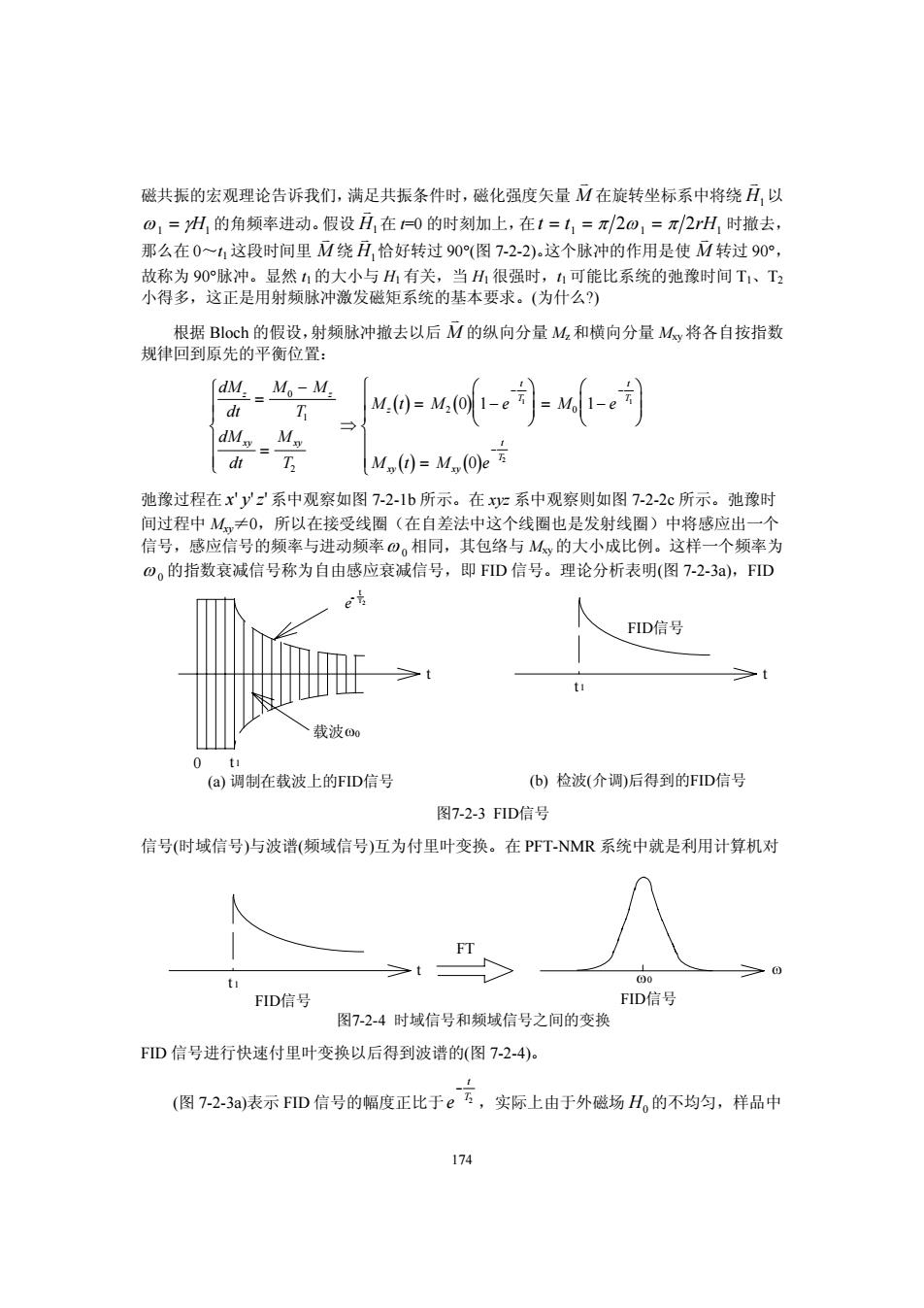
磁共振的宏观理论告诉我们,满足共振条件时,磁化强度矢量M在旋转坐标系中将绕H,以 o1=H的角频率进动。假设H,在0的时刻加上,在t=11=π/201=π/2rH时撤去, 那么在0~1这段时间里M绕H,恰好转过90(图7-2-2)。这个脉冲的作用是使M转过90°, 故称为90°脉冲。显然的大小与H有关,当H很强时,1可能比系统的弛豫时间T1、T2 小得多,这正是用射频脉冲激发磁矩系统的基本要求。(为什么?) 根据Bloch的假设,射频脉冲撤去以后M的纵向分量M,和横向分量My将各自按指数 规律回到原先的平衡位置: dM:M。-M dt T 0=o-月-司 M M(1)=M(O)e 弛豫过程在x'y'z系中观察如图7-2-1b所示。在xz系中观察则如图7-2-2c所示。弛豫时 间过程中M≠0,所以在接受线圈(在自差法中这个线圈也是发射线圈)中将感应出一个 信号,感应信号的频率与进动频率0。相同,其包络与M的大小成比例。这样一个频率为 o。的指数衰减信号称为自由感应衰减信号,即FD信号。理论分析表明(图7-2-3),FID FID信号 载波00 0t1 (a)调制在载波上的FID信号 (b)检波(介调)后得到的FID信号 图7-2-3FID信号 信号(时域信号)与波谱(频域信号)互为付里叶变换。在PFT-NMR系统中就是利用计算机对 -0 00 FID信号 FID信号 图7-2-4时域信号和频域信号之间的变换 FD信号进行快速付里叶变换以后得到波谱的(图7-24)。 (图7-2-3a)表示FID信号的幅度正比于e及,实际上由于外磁场H。的不均匀,样品中 174
174 磁共振的宏观理论告诉我们,满足共振条件时,磁化强度矢量 K M 在旋转坐标系中将绕 K H1以 ω γ 1 1 = H 的角频率进动。假设 K H1在 t=0 的时刻加上,在t t rH = 11 1 = π 2 2 ω = π 时撤去, 那么在 0~t1 这段时间里 K M 绕 K H1恰好转过 90°(图 7-2-2)。这个脉冲的作用是使 K M 转过 90°, 故称为 90°脉冲。显然 t1 的大小与 H1 有关,当 H1 很强时,t1 可能比系统的弛豫时间 T1、T2 小得多,这正是用射频脉冲激发磁矩系统的基本要求。(为什么?) 根据 Bloch 的假设,射频脉冲撤去以后 K M 的纵向分量 Mz和横向分量 Mxy将各自按指数 规律回到原先的平衡位置: () ( ) () ( ) dM dt M M T dM dt M T Mt M e M e Mt M e z z xy xy z t T t T xy xy t T = − = ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ ⇒ = − ⎛ ⎝ ⎜ ⎜ ⎞ ⎠ ⎟ ⎟ = − ⎛ ⎝ ⎜ ⎜ ⎞ ⎠ ⎟ ⎟ = ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ − − − 0 1 2 2 0 01 1 0 1 1 2 弛豫过程在 x' '' y z 系中观察如图 7-2-1b 所示。在 xyz 系中观察则如图 7-2-2c 所示。弛豫时 间过程中 Mxy≠0,所以在接受线圈(在自差法中这个线圈也是发射线圈)中将感应出一个 信号,感应信号的频率与进动频率ω 0 相同,其包络与 Mxy的大小成比例。这样一个频率为 ω 0 的指数衰减信号称为自由感应衰减信号,即 FID 信号。理论分析表明(图 7-2-3a),FID 信号(时域信号)与波谱(频域信号)互为付里叶变换。在 PFT-NMR 系统中就是利用计算机对 FID 信号进行快速付里叶变换以后得到波谱的(图 7-2-4)。 (图 7-2-3a)表示 FID 信号的幅度正比于e t T − 2 ,实际上由于外磁场 H0 的不均匀,样品中 载波 0 t 1 ω0 t e - t T2 t t 1 FID信号 (a) 调制在载波上的FID信号 (b) 检波(介调)后得到的FID信号 图7-2-3 FID信号 t t 1 FID信号 FT ω ω0 FID信号 图7-2-4 时域信号和频域信号之间的变换

不同核磁矩所处场大小不同,衰减时进动频率不相同,不同进动频率的指数衰减信号叠加 的结果使总和的FD信号以T2"衰减,T2"满足 111 TLT 其中五是Bloch定义的横向弛豫时间,而T,则反映了外场H,的不均匀T,一 -)。T2 H 的作用相当于使上能级的寿命缩短,从而使谱线展宽,用NMR方法通过测量线宽来计算 T2时实际上将T2'的影响也包含进去了。对液体样品来说,T2'常比T2要小得多,所以用线 宽来衡量T2是不合适的,以下我们将看到自旋回波技术就可以避免T2'的影响。 2.自旋回波(Spin Echo) 和自由感应衰减一样,自旋回波也可以用矢量模型来解释。 ≥y M t=0 tt (a) (b) (c) M M t=t+2ti =2r (d) (e) 图7-2-590°-t-180°自旋回波矢量图解 设磁场不太均匀,T2"<T2,观察自旋回波时用两个射频脉冲,第一个从=0到=1的是 “90°脉冲”,在τ时刻(T2"<t<T1,T2)加上第二个“180°脉冲”(脉冲持续时间比第一个 长一倍),我们来分析这时M的运动。在图7-2-5中,(a)是=0的情况,(b)是=时的情况。 M绕丑进动90,到达x'-y面上的y轴,随后可接收到自由进动信号,它以时间常数T2” 衰减至零(图7-2-6)。这个过程相当于不同磁场处的局部磁化强度矢量M,在x-y平面上分 散成均匀分布。这分散主要不是由于自旋一自旋弛豫作用,而是由于外磁场的不均匀。我 175
175 不同核磁矩所处场大小不同,衰减时进动频率不相同,不同进动频率的指数衰减信号叠加 的结果使总和的 FID 信号以 T2"衰减,T2"满足 1 11 T2 T2 T2 " ' = + 其中 T2 是 Bloch 定义的横向弛豫时间,而 T2',则反映了外场 H0 的不均匀(T2'= 1 0 γΔH )。T2' 的作用相当于使上能级的寿命缩短,从而使谱线展宽,用 NMR 方法通过测量线宽来计算 T2 时实际上将 T2'的影响也包含进去了。对液体样品来说,T2'常比 T2 要小得多,所以用线 宽来衡量 T2 是不合适的,以下我们将看到自旋回波技术就可以避免 T2'的影响。 2. 自旋回波(Spin Echo) 和自由感应衰减一样,自旋回波也可以用矢量模型来解释。 设磁场不太均匀,T2"<T2,观察自旋回波时用两个射频脉冲,第一个从 t=0 到 t=t1 的是 “90°脉冲”,在τ时刻(T2"<τ<<T1,T2)加上第二个“180°脉冲”(脉冲持续时间比第一个 长一倍),我们来分析这时 K M 的运动。在图 7-2-5 中,(a)是 t=0 的情况,(b)是 t=t1 时的情况。 K M 绕 K H1进动 90,到达 x' ' −y 面上的 y' 轴,随后可接收到自由进动信号,它以时间常数 T2" 衰减至零(图 7-2-6)。这个过程相当于不同磁场处的局部磁化强度矢量 K Mi 在 x' ' −y 平面上分 散成均匀分布。这分散主要不是由于自旋⎯自旋弛豫作用,而是由于外磁场的不均匀。我 z' y' x' 0 t=0 M0 M B1 (a) z' y' x' 0 t=t1 M (b) z' y' x' t=t1 M2 M1 t=τ (c) z' y' x' M'2 M'1 t=τ (d) +2 z' y' x' M t=2τ (e) 0 图7-2-5 90 180 o −τ − o自旋回波矢量图解 t1
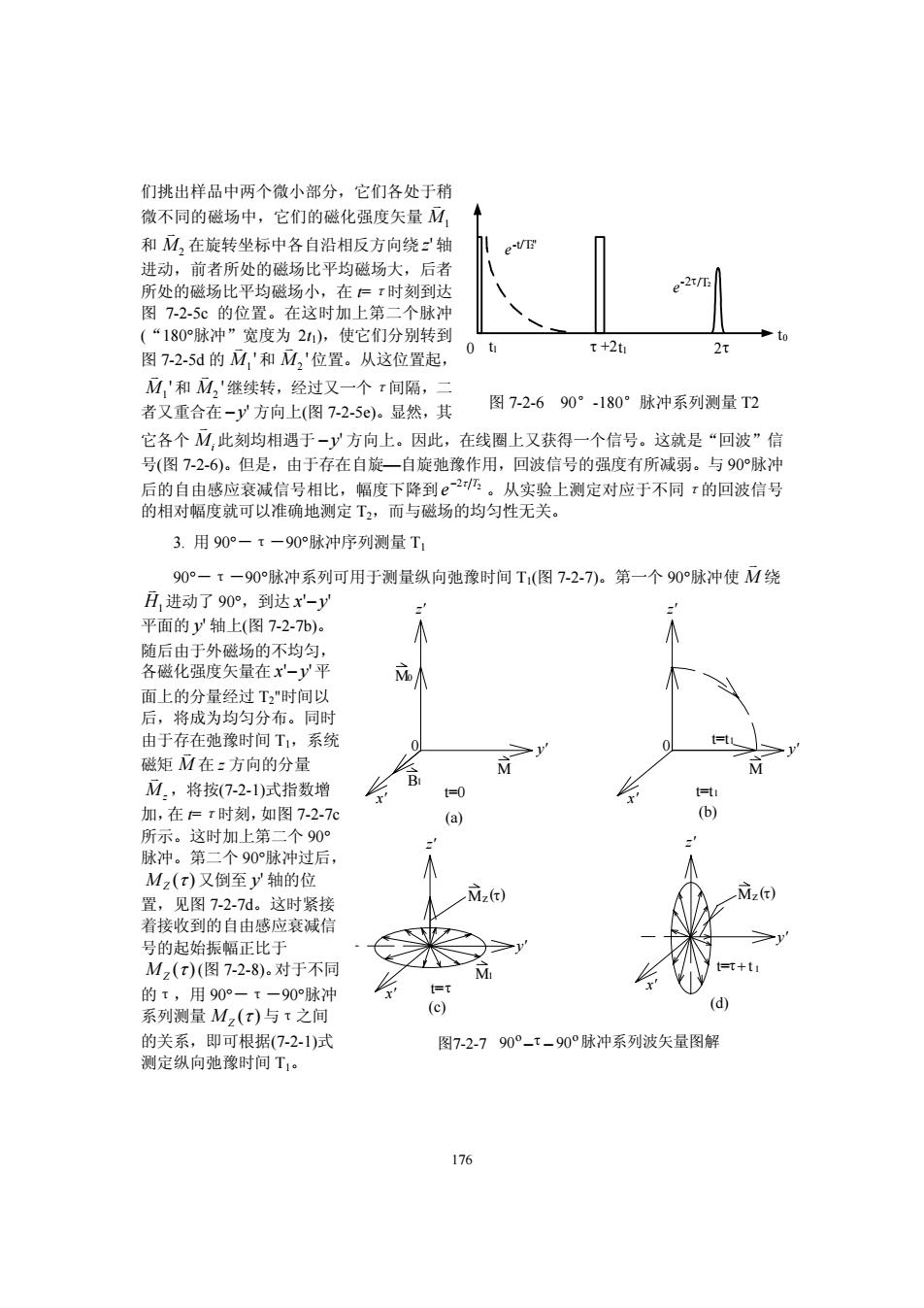
们挑出样品中两个微小部分,它们各处于稍 微不同的磁场中,它们的磁化强度矢量M, 和M,在旋转坐标中各自沿相反方向绕z轴 e-VT 进动,前者所处的磁场比平均磁场大,后者 所处的磁场比平均磁场小,在仁t时刻到达 图7-2-5c的位置。在这时加上第二个脉冲 (“180脉冲”宽度为21),使它们分别转到 0 t t +2t 2t 图7-2-5d的M,'和M,'位置。从这位置起, M,'和M,'继续转,经过又一个t间隔,二 者又重合在-y方向上(图7-2-5e)。显然,其 图7-2-690°-180°脉冲系列测量T2 它各个M,此刻均相遇于-y方向上。因此,在线圈上又获得一个信号。这就是“回波”信 号(图7-2-6)。但是,由于存在自旋一自旋弛豫作用,回波信号的强度有所减弱。与90°脉冲 后的自由感应衰减信号相比,幅度下降到2。从实验上测定对应于不同x的回波信号 的相对幅度就可以准确地测定T2,而与磁场的均匀性无关。 3.用90°一T一90°脉冲序列测量T1 90°一τ一90°脉冲系列可用于测量纵向弛豫时间T(图7-2-7)。第一个90°脉冲使M绕 丑进动了90°,到达x'-y 平面的y轴上(图7-2-7b)。 随后由于外磁场的不均匀, 各磁化强度矢量在x'-y平 面上的分量经过T2"时间以 后,将成为均匀分布。同时 由于存在弛豫时间T,系统 0 磁矩M在:方向的分量 M.,将按(7-2-1)式指数增 B t=0 t=t 加,在仁t时刻,如图7-2-7c (a) (b) 所示。这时加上第二个90 脉冲。第二个90°脉冲过后, Mz(t)又倒至y轴的位 置,见图7-2-7d。这时紧接 Mz(t) àz) 着接收到的自由感应衰减信 号的起始振幅正比于 M2(t)(图7-2-8)。对于不同 M =t+t 的T,用90°-t-90°脉冲 t=t 系列测量M2(x)与t之间 (c) (d) 的关系,即可根据(7-2-1)式 图7-2-790°-t-90°脉冲系列波矢量图解 测定纵向弛豫时间T1。 176
176 们挑出样品中两个微小部分,它们各处于稍 微不同的磁场中,它们的磁化强度矢量 K M1 和 K M2 在旋转坐标中各自沿相反方向绕 z' 轴 进动,前者所处的磁场比平均磁场大,后者 所处的磁场比平均磁场小,在 t=τ时刻到达 图 7-2-5c 的位置。在这时加上第二个脉冲 (“180°脉冲”宽度为 2t1),使它们分别转到 图 7-2-5d 的 K M1 '和 K M2 '位置。从这位置起, K M1 '和 K M2 '继续转,经过又一个τ间隔,二 者又重合在 −y' 方向上(图 7-2-5e)。显然,其 它各个 K Mi 此刻均相遇于 −y' 方向上。因此,在线圈上又获得一个信号。这就是“回波”信 号(图 7-2-6)。但是,由于存在自旋⎯自旋弛豫作用,回波信号的强度有所减弱。与 90°脉冲 后的自由感应衰减信号相比,幅度下降到e −2 T2 τ 。从实验上测定对应于不同τ的回波信号 的相对幅度就可以准确地测定 T2,而与磁场的均匀性无关。 3. 用 90°-τ-90°脉冲序列测量 T1 90°-τ-90°脉冲系列可用于测量纵向弛豫时间 T1(图 7-2-7)。第一个 90°脉冲使 K M 绕 K H1进动了 90°,到达 x' ' −y 平面的 y' 轴上(图 7-2-7b)。 随后由于外磁场的不均匀, 各磁化强度矢量在 x' ' −y 平 面上的分量经过 T2"时间以 后,将成为均匀分布。同时 由于存在弛豫时间 T1,系统 磁矩 K M 在 z 方向的分量 K Mz ,将按(7-2-1)式指数增 加,在 t=τ时刻,如图 7-2-7c 所示。这时加上第二个 90° 脉冲。第二个 90°脉冲过后, MZ ( ) τ 又倒至 y' 轴的位 置,见图 7-2-7d。这时紧接 着接收到的自由感应衰减信 号的起始振幅正比于 MZ ( ) τ (图 7-2-8)。对于不同 的τ,用 90°-τ-90°脉冲 系列测量 MZ ( ) τ 与τ之间 的关系,即可根据(7-2-1)式 测定纵向弛豫时间 T1。 0 t1 2τ t0 e-t/T"2 τ +2t1 e-2τ/T2 图 7-2-6 90°-180°脉冲系列测量 T2 z' y' x' 0 t=0 M0 M B1 (a) z' y' x' 0 t=t1 M (b) z' y' x' t=t1 Mz M1 t=τ (c) z' y' x' t=τ (d) + 图7-2-7 90 90 o −τ − o脉冲系列波矢量图解 t 1 ( ) τ Mz ( ) τ

二、实验装置 实验装置如图7-2-9所示。 脉冲程序器用于产生90°一τ一180°或 90°一t一90°脉冲序列,两个脉冲的宽度、 间隔及脉冲序列的重复频率均可调。射频发 正比于z() 射机在脉冲序列的控制下发送频率为⊙。 ≥t tt+2ti 的射频脉冲序列去激励样品。仪器使用单线 图7-2-890°-τ-90°脉冲系列测量T1 圈探头,发射和接收由同一个线圈完成,探 头还包括调配电路和由二极管构成的自动开关,使发射和接收都能工作在良好的状态下。 接收放大器包括射频放大、检波和低频放大,输出信号送到示波器观察,同时送到一个单 点取样积分器,积分后用表头指示回波幅度。取样位置由来自脉冲程序器的取样脉冲控制。 脉冲程序器还输出一个同步脉冲作为示波器x轴的触发信号。 单点取 样积分 表头 回波信号 接收探头 脉,冲 射频 接收 程序器 发射机 放大器 同步脉冲 图7-2-9自旋回波实验装置 三、实验内容和要求 1.熟悉仪器,观察脉冲序列波形和射频冲序列波形,了解脉冲宽度、间隔及重复周期 的调节方法及调节范围。 2.观察甘油样品的FD信号 提示:①测量射频脉冲频率0o,利用共振条件及H的旋磁比数值Y=26753rad/S·G 计算Ho,并设定Ho(以后还需细调)。②适当选取脉冲间隔τ及周期T。 3.观察甘油样品的自旋回波信号 注意:不满足90°一τ一180°脉冲序列时也会看到回波信号,但90°一T一180°脉冲序列 作用下回波信号最强。 177
177 二、 实验装置 实验装置如图 7-2-9 所示。 脉冲程序器用于产生 90°-τ-180°或 90°-τ-90°脉冲序列,两个脉冲的宽度、 间隔及脉冲序列的重复频率均可调。射频发 射机在脉冲序列的控制下发送频率为ω 0 的射频脉冲序列去激励样品。仪器使用单线 圈探头,发射和接收由同一个线圈完成,探 头还包括调配电路和由二极管构成的自动开关,使发射和接收都能工作在良好的状态下。 接收放大器包括射频放大、检波和低频放大,输出信号送到示波器观察,同时送到一个单 点取样积分器,积分后用表头指示回波幅度。取样位置由来自脉冲程序器的取样脉冲控制。 脉冲程序器还输出一个同步脉冲作为示波器 x 轴的触发信号。 三、实验内容和要求 1. 熟悉仪器,观察脉冲序列波形和射频冲序列波形,了解脉冲宽度、间隔及重复周期 的调节方法及调节范围。 2. 观察甘油样品的 FID 信号 提示:①测量射频脉冲频率ω 0 ,利用共振条件及 H 的旋磁比数值γH=26753rad/S·G 计算 H0,并设定 H0(以后还需细调)。②适当选取脉冲间隔τ及周期 T。 3. 观察甘油样品的自旋回波信号 注意:不满足 90°-τ-180°脉冲序列时也会看到回波信号,但 90°-τ-180°脉冲序列 作用下回波信号最强。 0 t1 τ τ+2t1 t 图7-2-8 90 90 o o − −τ 脉冲系列测量T1 e-t/T"2 正比于Mz ( ) τ S N 接 收 放大器 单点取 样积分 射 频 发射机 脉 冲 程序器 Y X 表头 回波信号 接收探头 同步脉冲 图7-2-9 自旋回波实验装置