
第一章矢量分析 即数学中的“场论” 主要内容: S1.1基本概念 §1.2无旋场、无散场及矢量场的分解 §1.37算子的运算 S1.4积分定理 §1.56函数
第 章一 矢量分析 即数学中的“场论” 主要内容: §1.1 基本概念 §1.2 无旋场、无散场及矢量场的分解 §1 3. 算子的运算 §1.4 积分定理 §1.5 δ 函数

§1.1基本概念 场的定义: 一个物理量或数学量在空间的分布称为该物理量或数 学量的场。即:若对空间某一区域内的任意点,都有 某个物理量或数学量的一个确定值与之对应,则称该 区域内确定了该物理量或数学量的一个场。 数学上,场《函数(自变量为空间坐标) 标量场(Scalar Field) 场 矢量场(Vector Field) 备注:场可随时间变化,但数学中的场论仅研 究其随空间的变化
§1.1 基本概念 场的定义: 一个物理量或数学量在空间的分布称为该物理量或数 学量的场。即:若 某 域内的任意点 若对空间某一区域内的任意点,都有 某个物理量或数学量的一个确定值与之对应,则称该 区域内确定了该物理量或数学量的 个场 区域内确定了该物理量或数学量的一个场。 数学上,场 函数(自变量为空间坐标 自变量为空间坐标) 场 标量场(Scalar Field) 矢量场(Vector Field) 备注:场可随时间变化,但数学中的场论仅研 究其随空间的变化
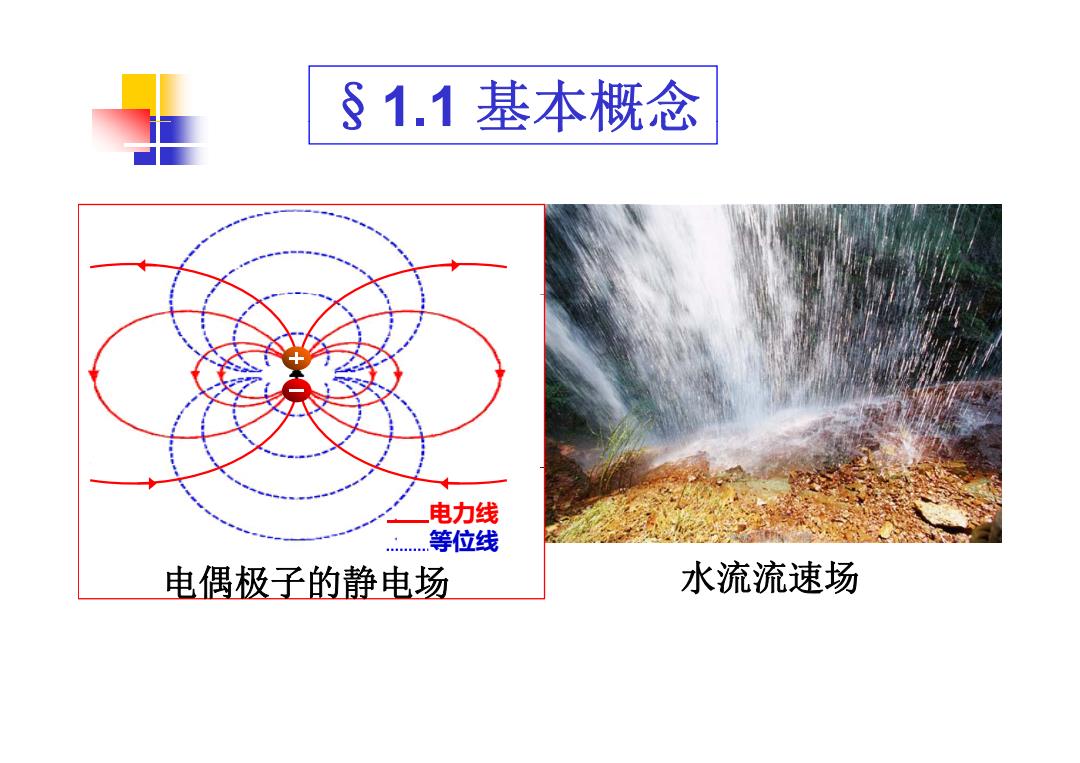
§1.1基本概念 电力线 等位线 电偶极子的静电场 水流流速场
§1.1 基本概念 等位线 电力线 电偶极子的静电场 水流流速场
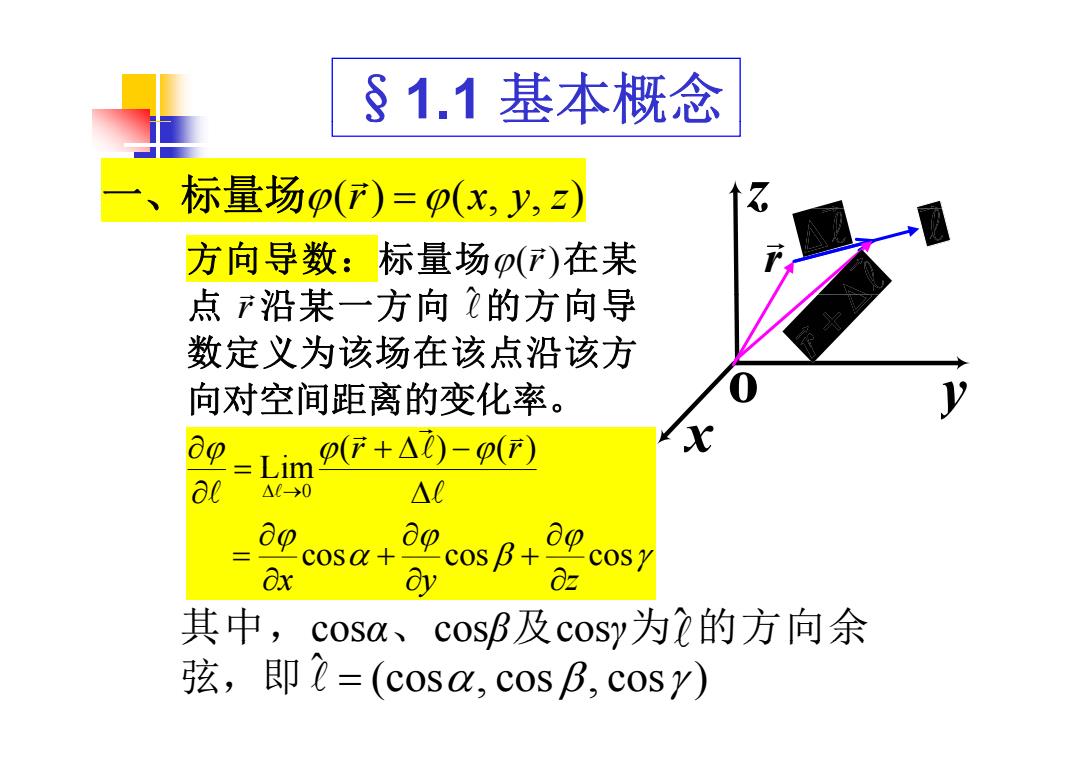
§1.1基本概念 标量场p()=p(x,y,z) 方向导数:标量场0()在某 点沿某一方向的方向导 数定义为该场在该点沿该方 向对空间距离的变化率。 ∂0 Lim p(行+△C)-p(F) al △0→0 △U 0 cosa 8x op cosB+ 8y osy 8z 其中, c0S0、 cosB及cosy为)的方向余 弦,即C=(cosa,cosB,cosY)
§1.1 基本概念 一 、标量场(r) (x, y, z) 、标量场(r) (x, y, z) z 方向导数:标量场 (r) 在某 点 沿某 方向 ˆ 的方向导 z r 点 r沿某一方向 的方向导 数定义为该场在该点沿该方 o ( ) ( ) Lim r r 向对空间距离的变化率。 o x y cos cos cos Lim 0 cos cos cos x y z 其中,cosα、cosβ及cosγ为ˆ 的方向余 弦,即 (cos , cos , cos ) ˆ

§1.1基本概念 梯度:标量场在某点的梯度为一矢量。 其大小等于该点所有方向导数的最大 值,其方向为取得该最大值的方向。 -gadp.t-与i的夹角 其中,grado即为梯度: grado ∂x gradient Nabla或Hamilton算子,读作“del
§1.1 基本概念 标量场在某点的梯度为一矢量 §1.1 基本概念 梯 度:标量场在某点的梯度为 矢量。 其大小等于该点所有方向导数的最大 梯 度: 值,其方向为取得该最大值的方向。 ) d ˆ d ( d ˆ 与的夹角 grad grad cos(grad 与的夹角) 其中 d 即为梯度 d ˆ ˆ ˆ 其中,grad 即为梯度: z z y y x x grad ˆ ˆ ˆ gradient Nabla或Hamilton算子, 读作“del