I=112的核自旋能级裂分与H,的关系 。 由式E=一Ho及图可知H核在磁场中,由低能 级E向高能级E2跃迁,所需能量为 AE=E2-E=uHo -(-HHo)=2 uHo ·△E与核磁矩及外磁场强度成正比,H越大,能 级分裂越大,△E越大 H,外加磁场 m=-1/2E2=uH 无磁场 △E=2uH0 m=+1/2E=一Ho
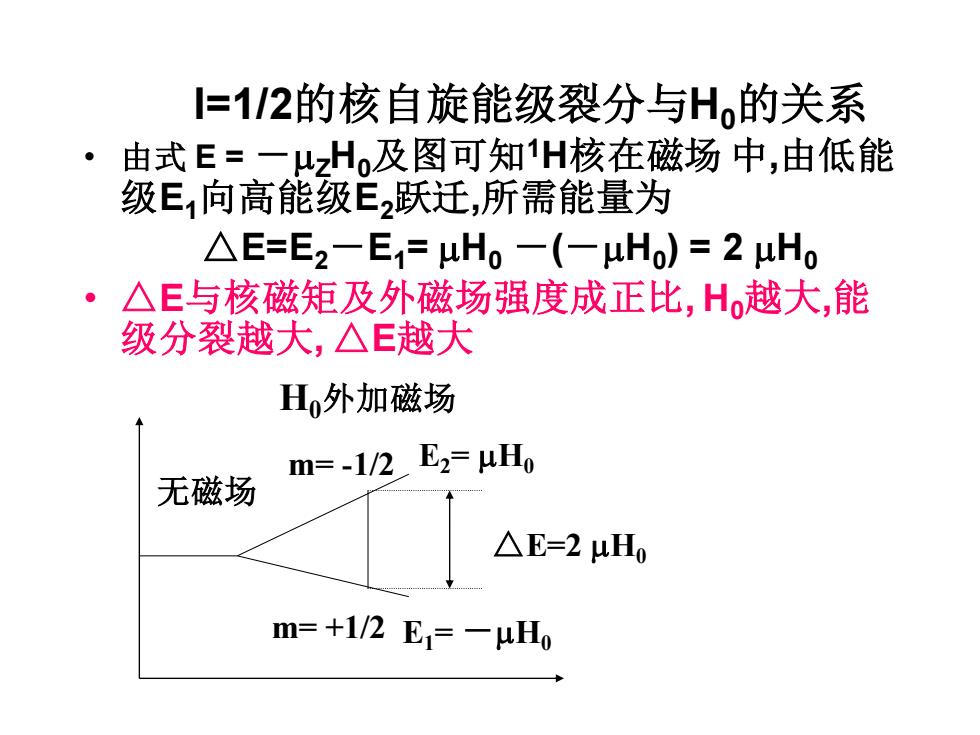
I=1/2的核自旋能级裂分与H0的关系 • 由式 E = -ZH0及图可知1H核在磁场 中,由低能 级E1向高能级E2跃迁,所需能量为 △E=E2-E1= H0 -(-H0 ) = 2 H0 • △E与核磁矩及外磁场强度成正比, H0越大,能 级分裂越大, △E越大 无磁场 H0外加磁场 E1= -H0 E2= H0 △E=2 H0 m= -1/2 m= +1/2

(二)原子核的共振吸收 。 如果以一定频率的电磁波照射处于磁场B,中的 核,且射频频率ν恰好满足下列关系时: hv=△E △E=2μB0 2uBo (核磁共振条件式) V= 自旋核的跃迁能量 h 高能级 磁性核 hv=△E 低能级 处于低能态的核将吸收射频能量而跃迁至高 能态,这种现象叫做核磁共振现象。 h u=m =1/2的核发生核磁共振吸收射频 2元 的频率,即共振频率
(二)原子核的共振吸收 • 如果以一定频率的电磁波照射处于磁场B0中的 核,且射频频率恰好满足下列关系时: • h =ΔE ΔE=2 B0 (核磁共振条件式) h 0 2 = ◼ 处于低能态的核将吸收射频能量而跃迁至高 能态,这种现象叫做核磁共振现象。 2 h = m I=1/2 的核发生核磁共振吸收射频 的频率,即共振频率。 自旋核的跃迁能量 磁性核 h =ΔE 高能级 低能级

y1h代入v=2B得 Bo 4=Y22π 2π 产生核磁共振光谱的条件 。(1)对自旋量子数=12的同一核来说, 因磁矩为一定值,Y一为常数,所以发生 共振时,照射频率的大小取决于外磁场 强度的大小。外磁场强度增加时,为使 核发生共振,照射频率也相应增加;反 之,则减小
• (1)对自旋量子数I=1/2的同一核来说,, 因磁矩为一定值,—为常数,所以发生 共振时,照射频率的大小取决于外磁场 强度的大小。外磁场强度增加时,为使 核发生共振,照射频率也相应增加;反 之,则减小。 2 0 代入 得 = h h 2 B0 2 2 1 = = 产生核磁共振光谱的条件

·例:外磁场B=4.69T(特斯拉,法定计量单位) ·H的共振频率为 v=YuBo_ 2.68×108T-1s1×4.69T 2π 2×3.14 =2.0015×108s1=200.15MHz (1s-=1Hz) 放在外磁场B。=2.35Tv=100MHz
• 例:外磁场B0=4.69T(特斯拉,法定计量单位) • 1H 的共振频率为 2.0015 10 200.15 (1 1 ) 2 3.14 2.68 10 4.69 2 8 1 1 8 1 1 0 s MHz s Hz s H = = = = = − − − − ◼ 放在外磁场 B0 =2.35T =100MHz

(2)对自旋量子数=112的不同核来说,若同时 放入一固定磁场中,共振频率取决于核本身磁 矩的大小,山大的核,发生共振所需的照射频率 也大;反之,则小。例:13C的共振频率为: y=B。 6.73×107T-1s1×4.69T 2π 2×3.14 =5.026×107s1=50.26MHz y=mB。=2.68×108T-s1×4.69T 2元 2×3.14 =2.0015×108s1=200.15MHz
• (2)对自旋量子数I=1/2的不同核来说,若同时 放入一固定磁场中,共振频率取决于核本身磁 矩的大小, 大的核,发生共振所需的照射频率 也大;反之,则小。例:13C的共振频率为: s MHz s c 5.026 10 50.26 2 3.14 6.73 10 4.69 2 7 1 7 1 1 0 = = = = − − − s MHz s H 2 0015 10 200 15 2 3 14 2 68 10 4 69 2 8 1 8 1 1 0 . . . . . = = = = − − −