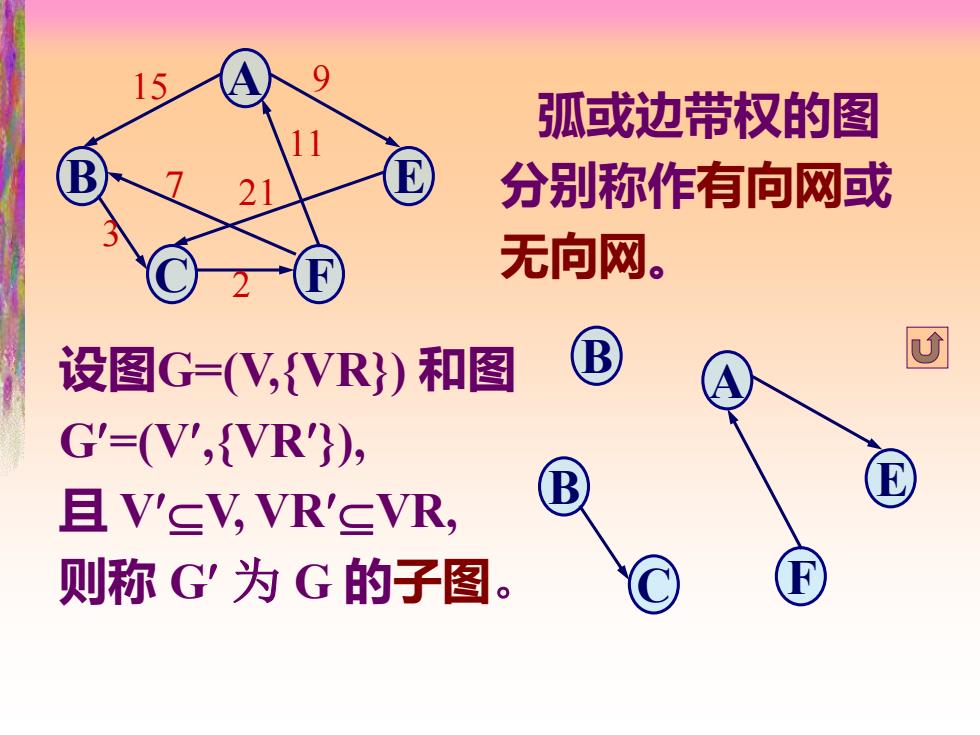
15 弧回或边带权的图 分别称作有向网或 无向网。 设图G=(V,{VR)和图 G'=(V',{VR}), 且V'sV,VR'sVR, 则称G为G的子图
A B E C F A E F B B C 设图G=(V,{VR}) 和图 G=(V,{VR}), 且 VV, VRVR, 则称 G 为 G 的子图。 15 9 7 21 11 3 2 弧或边带权的图 分别称作有向网或 无向网

假设图中有n个顶点,e条边,则 含有e=n(n-1)/2条边的无向图称作完全图: 含有e=n(n-1)条弧的有向图称作有向完全图; 若边或弧的个数e<nlogn,则称作稀疏图 否则称作稠密图。 回
含有 e=n(n-1)/2 条边的无向图称作完全图; 含有 e=n(n-1) 条弧的有向图称作有向完全图; 若边或弧的个数 e<nlogn,则称作稀疏图, 否则称作稠密图。 假设图中有n个顶点,e条边,则
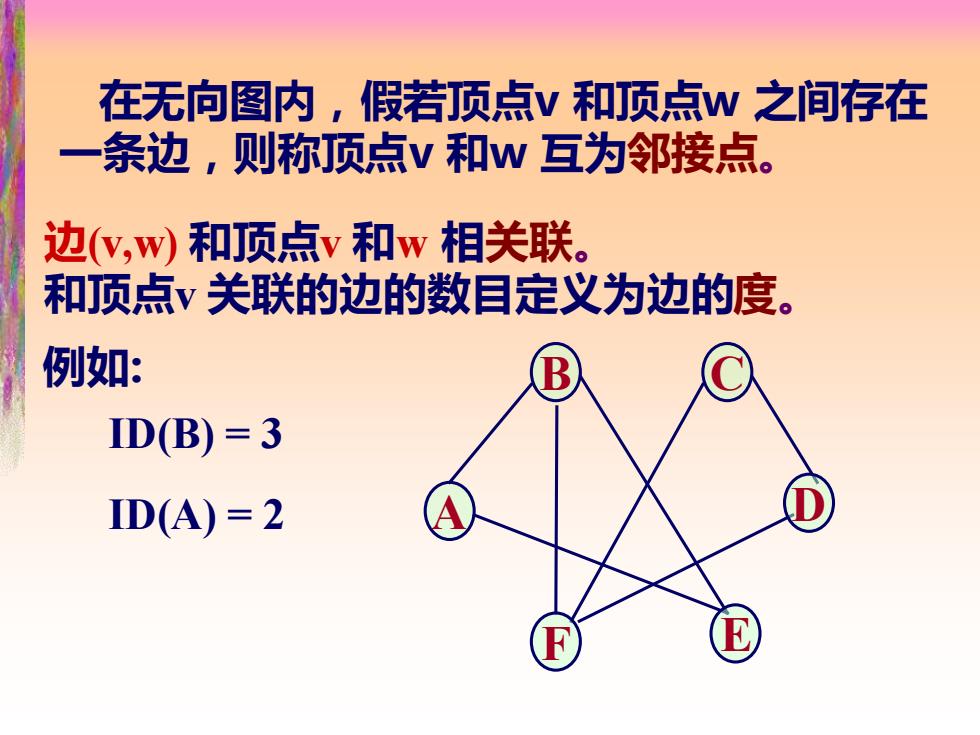
在无向图内,假若顶点V和顶点w之间存在 条边,则称顶点v和w互为邻接点。 边y,w)和顶点v和w相关联。 和顶点v关联的边的数目定义为边的度。 例如: B ID(B)=3 D(A)=2
例如: ID(B) = 3 ID(A) = 2 边(v,w) 和顶点v 和w 相关联。 和顶点v 关联的边的数目定义为边的度。 A C D F E B 在无向图内,假若顶点v 和顶点w 之间存在 一条边,则称顶点v 和w 互为邻接点
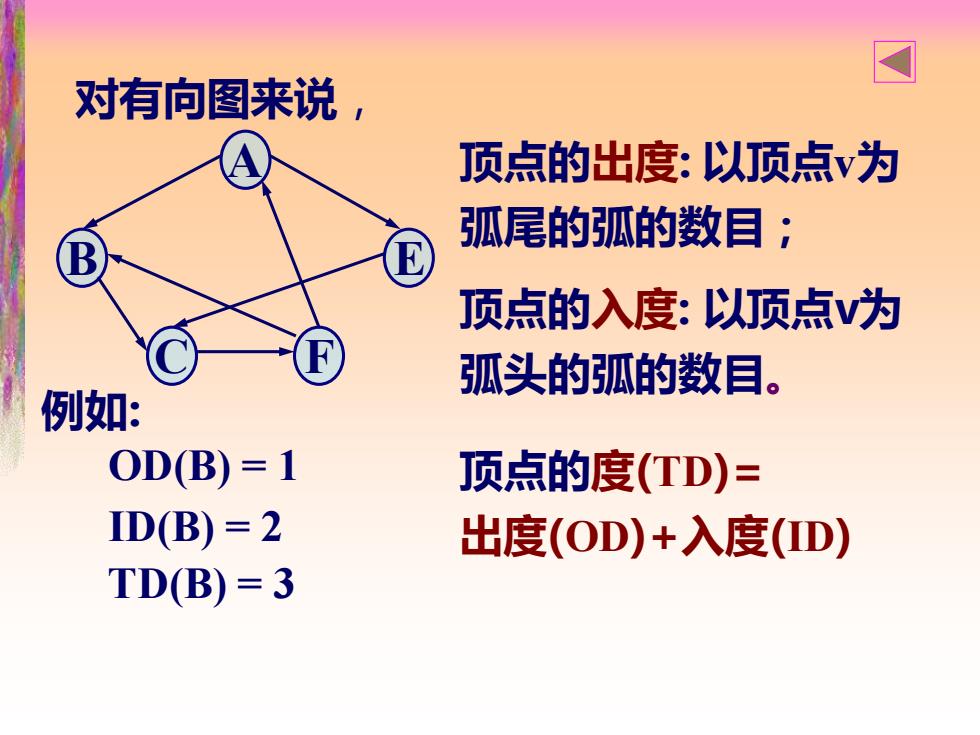
网 对有向图来说, 顶点的出度:以]顶点v为 弧尾的弧的数目; 顶点的入度:以]顶点为 弧头的弧的数目。 例如: OD(B)=1 顶点的度(TD)= ID(B)=2 出度(OD)+入度(D) TD(B)=3
顶点的出度: 以顶点v为 弧尾的弧的数目; A B E C F 顶点的入度: 以顶点v为 弧头的弧的数目。 顶点的度(TD)= 出度(OD)+入度(ID) 例如: ID(B) = 2 OD(B) = 1 TD(B) = 3 对有向图来说
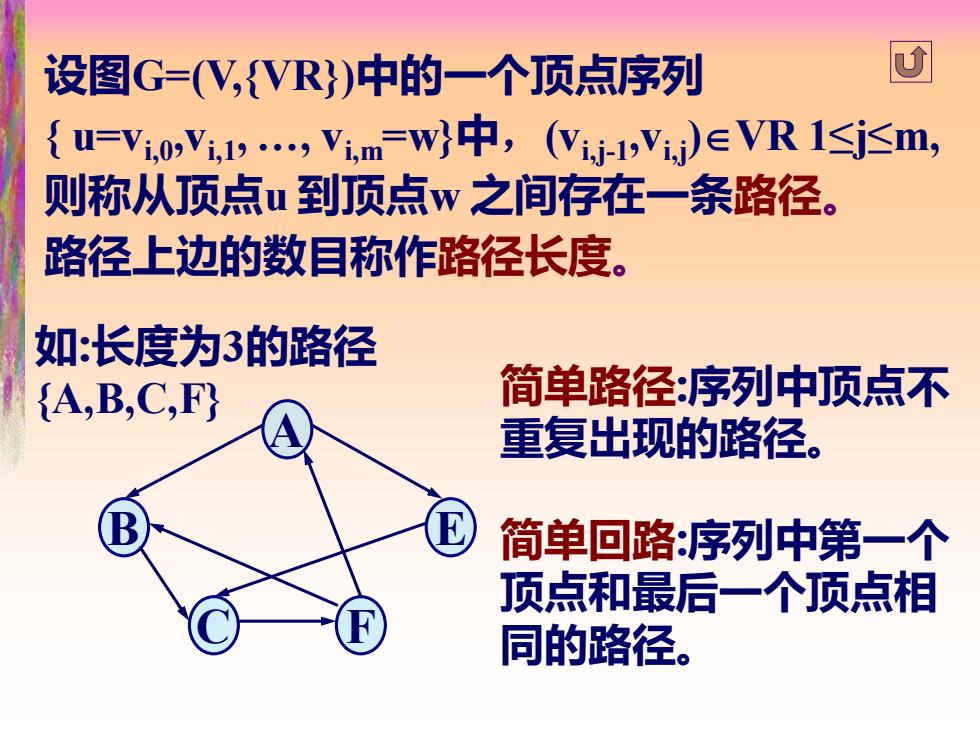
设图G=(V,{VR)中的一个顶点序列 团 {u=V.0Y,,Vm=wy中,(Wi-1V)eVR1≤jm, 则称从顶点u到顶点w之间存在一条路径。 路径上边的数目称作路径长度。 如:长度为3的路径 (A,B,C,F} 简单路径:序列中顶点不 重复出现的路径。 简单回路:序列中第一个 顶点和最后一个顶点相 同的路径
设图G=(V,{VR})中的一个顶点序列 { u=vi,0,vi,1, …, vi,m=w}中,(vi,j-1 ,vi,j)VR 1≤j≤m, 则称从顶点u 到顶点w 之间存在一条路径。 路径上边的数目称作路径长度。 A B E C F 如:长度为3的路径 {A,B,C,F} 简单路径:序列中顶点不 重复出现的路径。 简单回路:序列中第一个 顶点和最后一个顶点相 同的路径