
根据描述体系性质的物理量与体系中物质的量的关系。 一类具有广度性质的状态函数,如:V、n、m、 u、H、S、G等。这类性质具有加合性。 状态 函数 另一类具有强度性质的状态函数,如:T、P、P、 等。这类性质没有加合性。 研究状态和状态函数时应注意两点: 1.描述一个系统所处的状态时,不必将所有的状态函 数全部列出,通常只选择几个易于测定的相互独立的状态 函数来描述系统的状态。如;PV=nRT 2.状态函数的变化值只取决于状态变化的始态和终 态,而与变化的途径天关。如:50g50C的水(始态)加 热变为50g80C的水(终态)。 △T=T(终态)-T(始态)=30℃
根据描述体系性质的物理量与体系中物质的量的关系。 一类具有广度性质的状态函数,如:V、n、m、 u、H、S、G 等。这类性质具有加合性。 另一类具有强度性质的状态函数,如:T、P、ρ、 等。这类性质没有加合性。 研究状态和状态函数时应注意两点: 1.描述一个系统所处的状态时,不必将所有的状态函 数全部列出,通常只选择几个易于测定的相互独立的状态 函数来描述系统的状态。如;PV=nRT 2.状态函数的变化值只取决于状态变化的始态和终 态,而与变化的途径无关。如:50g 50ºC的水(始态)加 热变为50g 80ºC的水(终态)。 ΔT = T (终态)-T (始态)= 30ºC。 状态 函数

(三)过程和途径 体系从一种状态变到另一种状态称为经历了一个过程。 等温过程(isothermal process)△T=0 等压过程(isobar process)△P=0 过程 等容过程(isovolumic process)△V=0 绝热过程(adiabatic process)△Q=0 途径完成一个热力学过程,可以采取多种不同的方式。 我们把每种具体的方式,称为一种途径。 过程着重于始态和终态;而途径着重于具体方式
(三)过程和途径 体系从一种状态变到另一种状态称为经历了一个过程。 过程 等温过程(isothermal process) ΔT = 0 等压过程(isobar process) ΔP = 0 等容过程(isovolumic process) ΔV = 0 绝热过程(adiabatic process) ΔQ = 0 途径 完成一个热力学过程,可以采取多种不同的方式。 我们把每种具体的方式,称为一种途径。 过程着重于始态和终态;而途径着重于具体方式
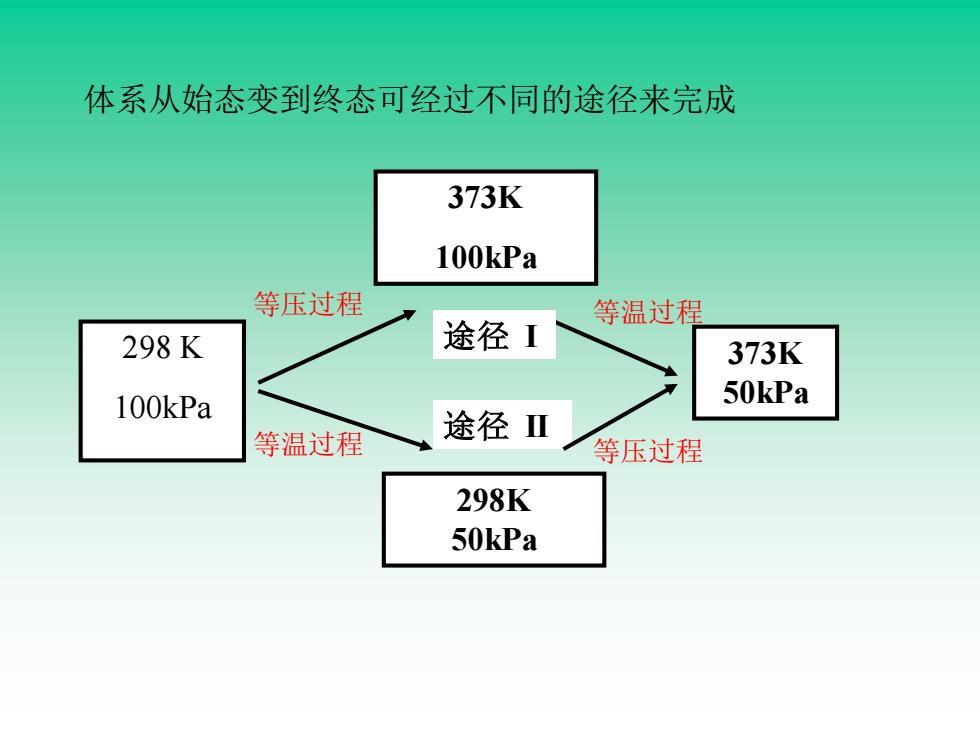
体系从始态变到终态可经过不同的途径来完成 373K 100kPa 等压过程 等温过程 298K 途径I 373K 100kPa 50kPa 等温过程 途径Ⅱ 等压过程 298K 50kPa
体系从始态变到终态可经过不同的途径来完成 途径 I 373K 100kPa 373K 50kPa 298 K 100kPa 途径 II 298K 50kPa 等压过程 等温过程 等压过程 等温过程

二、热力学第一定律 (一)热和功 在热力学中,热(heat)是系统和环境之间由于温度差 而交换的能量形式,常用符号“Q”表示。体系和环境之间 除了热以外的一切能量交换形式统称为功(wOk),常用 符号“W”表示。 系统向环境放热,Q为负值,即Q<0; 系统从环境吸热,Q为正值,即Q>0。 热力学规定: 系统对环境作功,W为负值,即W<O: 环境对系统作功,W为正值,即W>O。 热和功不是状态函数,热和功的变化数值与系统的变化 途径密切相关
二、热力学第一定律 (一)热和功 在热力学中,热(heat)是系统和环境之间由于温度差 而交换的能量形式,常用符号“Q”表示。体系和环境之间 除了热以外的一切能量交换形式统称为功(work),常用 符号“W”表示。 热力学规定: 系统向环境放热,Q为负值,即Q < 0; 系统从环境吸热,Q为正值,即Q > 0。 系统对环境作功,W为负值,即W< 0; 环境对系统作功, W为正值,即W> 0。 热和功不是状态函数,热和功的变化数值与系统的变化 途径密切相关
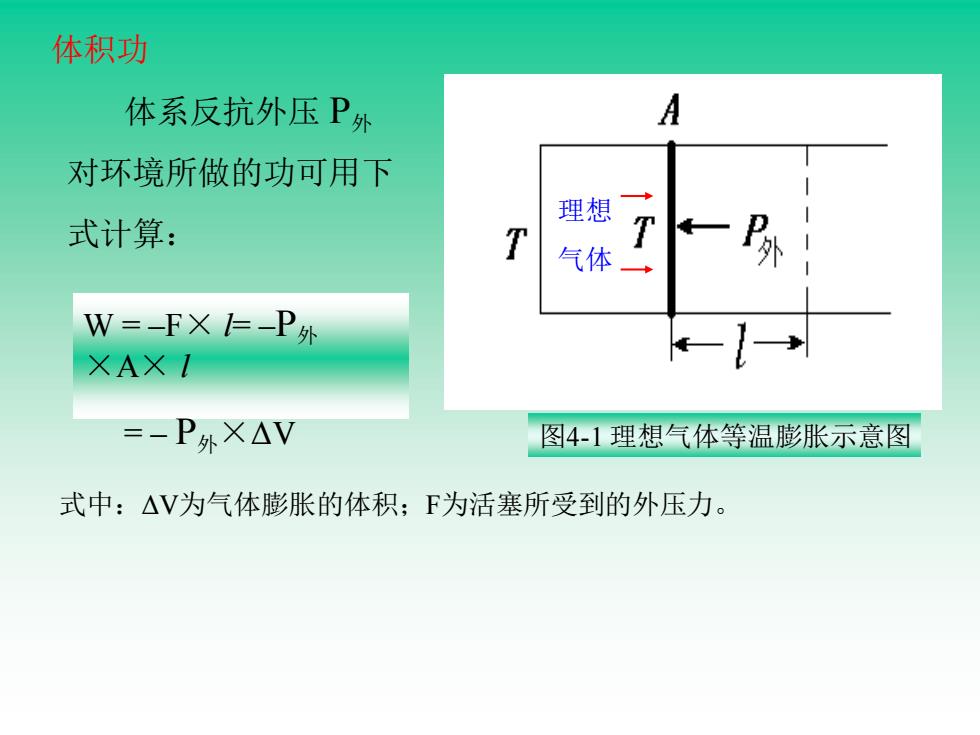
体积功 体系反抗外压P外 A 对环境所做的功可用下 理想 式计算: T 气体 W=-FX=-P外 XAXI =-P外X△V 图4-1理想气体等温膨胀示意图 式中:△V为气体膨胀的体积;F为活塞所受到的外压力
体积功 图4-1 理想气体等温膨胀示意图 理想 气体 体系反抗外压 P外 对环境所做的功可用下 式计算: W = –F× l= –P外 ×A× l = – P外×ΔV 式中:ΔV为气体膨胀的体积;F为活塞所受到的外压力