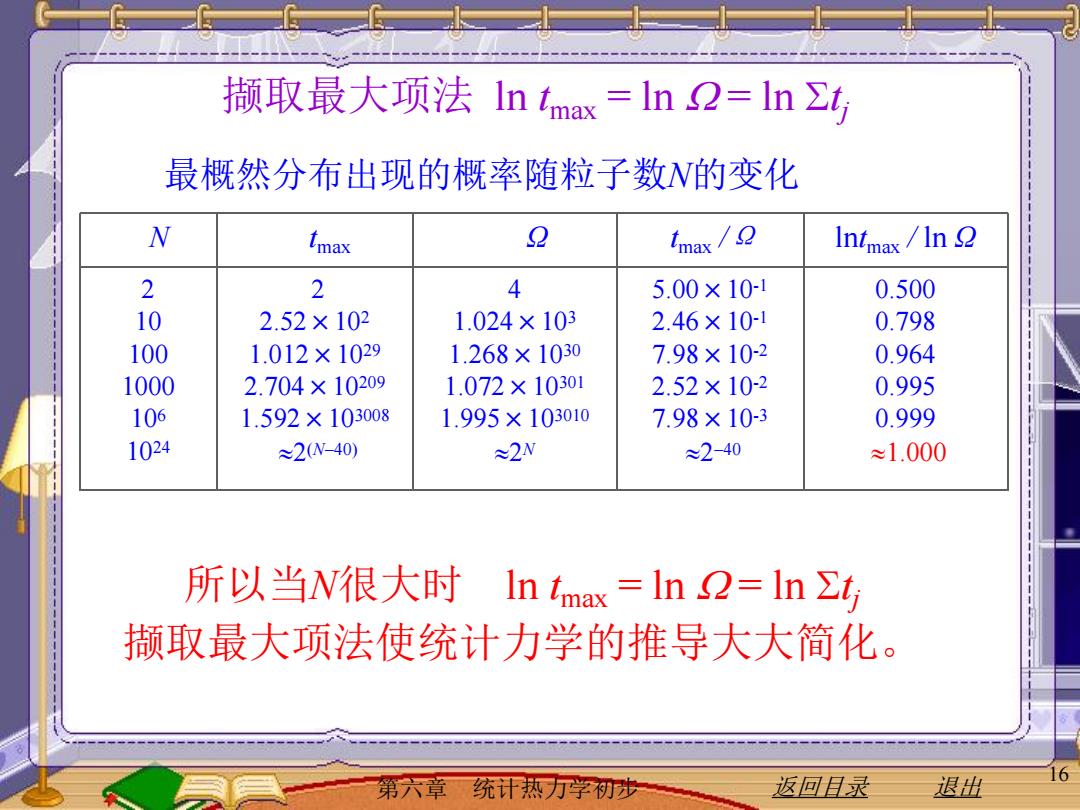
撷取最大项法In imax=ln2=ln∑t 最概然分布出现的概率随粒子数N的变化 N 2 Intmax /In 2 210 2 4 5.00×10-1 0.500 2.52×102 1.024×103 2.46×10-1 0.798 100 1.012×1029 1.268×1030 7.98×10-2 0.964 1000 2.704×10209 1.072×10301 2.52×10-2 0.995 10s 1.592×103008 1.995×103010 7.98×10-3 0.999 1024 ≈2W-40) ≈2N ≈2-40 ≈1.000 所以当N很大时 In tmax=ln2=ln∑t 撷取最大项法使统计力学的推导大大简化。 第六章 统计热万了学初光 返回目录 退出
第六章 统计热力学初步 返回目录 退出 16 撷取最大项法 ln tmax = ln = ln tj N tmax Ω tmax /Ω lntmax / ln Ω 2 10 100 1000 106 1024 2 2.52×10 2 1.012×1029 2.704×10209 1.592×103008 2 (N40) 4 1.024×10 3 1.268×1030 1.072×10301 1.995×103010 2 N 5.00×10-1 2.46×10 -1 7.98×10-2 2.52×10-2 7.98×10-3 2 40 0.500 0.798 0.964 0.995 0.999 1.000 最概然分布出现的概率随粒子数N的变化 所以当N很大时 ln tmax = ln = ln tj 撷取最大项法使统计力学的推导大大简化

例题1用量热法测得的CO气体的熵值与统计 热力学的计算结果不一致,这是由于在0K时CO分 子在其晶体中有两种可能的取向 CO或OC,因 此不满足热力学第三定律所要求的“完美晶体” 的条件,即0K时标准熵值不为零。试求算CO晶体 在0K时的摩尔熵值为若干? 解根据玻耳兹曼定理.在0K时, 完美晶体 中分子的空间取向都是相同的(即不可区分的), 因此其微观状态数21,故S=0。而CO晶体中的 分子既然可能有两种不同的空间取向,则其21, 故S≠0。 第六章 统计热力学初步 返回目录 退出
第六章 统计热力学初步 返回目录 退出 17 例题1 用量热法测得的CO气体的熵值与统计 热力学的计算结果不一致,这是由于在0K时CO分 子在其晶体中有两种可能的取向——CO或OC,因 此不满足热力学第三定律所要求的“完美晶体” 的条件,即0K时标准熵值不为零。试求算CO晶体 在0K时的摩尔熵值为若干? 解 根据玻耳兹曼定理.在0K时,完美晶体 中分子的空间取向都是相同的(即不可区分的), 因此其微观状态数=1,故S=0。而CO晶体中的 分子既然可能有两种不同的空间取向,则其≠1, 故S≠0

1molC0共有6.02×1023个分子,每个分子都可能 有两种空间取向,或是CO或是OC,因此其微观 状态数应为 2=26.02x102 S=kln2=(1.38×1023ln202x1o)J-K1 =5.76J.K-1 返回目录 8 第六章统计热力学初 退出
第六章 统计热力学初步 返回目录 退出 18 1mol CO共有6.0210 23个分子,每个分子都可能 有两种空间取向,或是CO或是OC,因此其微观 状态数应为 23 6.02 10 2 2 L 23 23 6.02 10 1 S k ln (1.38 10 ln 2 ) J K 1 5.76 J K

3.玻耳兹曼分布 决定系统宏观性质的是微观粒子的能量分布 能级:基态、激发态(量子化) OK时,都处于基态, >OK时,任一微观粒子都有从基态激发的倾向, 粒子在众多能级形成许多不同方式的分布 能级: e08182.ei… 简并度: 80 8182…8i… 种分布:no n1n2. ni... 第六章 统计热万学初光 返回目录 退出
第六章 统计热力学初步 返回目录 退出 19 3. 玻耳兹曼分布 决定系统宏观性质的是微观粒子的能量分布 能级:基态、激发态(量子化) 0K时,都处于基态, >0K时,任一微观粒子都有从基态激发的倾向, 能级: ε0 ε1 ε2 …εi … 简并度: g0 g1 g2 … gi… 一种分布: n0 n1 n2 … ni … 粒子在众多能级形成许多不同方式的分布

玻耳兹曼指出,在众多的分布中,微观状态数最 多的分布方式为: n 8,e-sl W >g e-slT (6.3) 上式即为玻耳兹曼分布。 式中: 8 :能级的能量值; gi 能级的简并度(具有相同能量的量子状态数): n:分配于能级的粒子数; N:系统中微观粒子总数: exp(-e,/kT):玻耳兹曼因子 第六章 统计热力学初光 返回目录 退出
第六章 统计热力学初步 返回目录 退出 20 玻耳兹曼指出,在众多的分布中,微观状态数最 多的分布方式为: / / e e i i kT i i kT i n g N g 上式即为玻耳兹曼分布。 式中: εi:i能级的能量值; gi:i能级的简并度(具有相同能量的量子状态数); ni : 分配于i能级的粒子数; N : 系统中微观粒子总数; exp(–εi /kT):玻耳兹曼因子 (6.3)