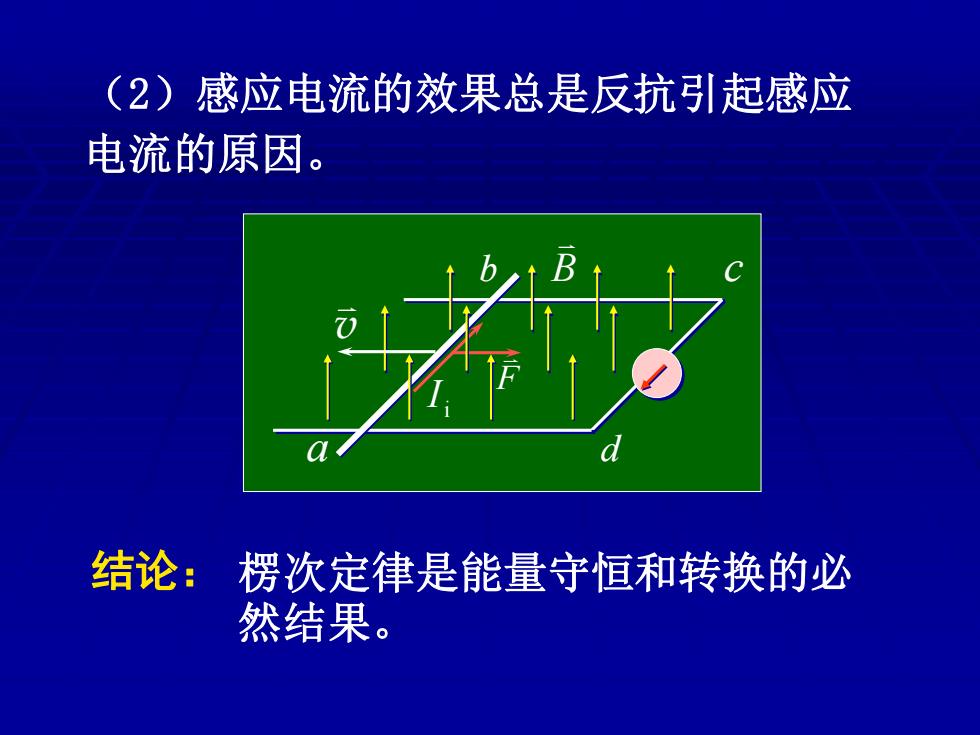
(2)感应电流的效果总是反抗引起感应 电流的原因。 结论: 楞次定律是能量守恒和转换的必 然结果
a b c d (2)感应电流的效果总是反抗引起感应 电流的原因。 i I F 楞次定律是能量守恒和转换的必 然结果。 结论: B v

例1一长直导线通以电流i=I。snot,旁边有一 个共面的矩形线圈abcd。求:线圈中的感应电动势。 解: o8- b 4o102 sin ot+☑ 2 dΦ E dt 4n0 lwcos@tIn +☑ 2π
解: 例1 一长直导线通以电流 ,旁边有一 个共面的矩形线圈abcd。求:线圈中的感应电动势。 i I sin t = 0 O 1 l 2 l d b c a r x i x dx + = = 1 d 2π d 2 0 r l S r l x x i Φ B S r r l t I l 0 0 2 1 sin ln 2π + = t Φ i d d = − r r l l t I 1 2 0 0 cos ln 2π + = −

§8.2 动生电动势, 感生电动势 根据磁通量变化的不同原因,把感应电动势 分为两种情况加以讨论。 动生电动势:在稳恒磁场中运动着的导体内产 生的感应电动势。 感生电动势:导体不动,因磁场的变化产生的 感应电动势。 注意:动生电动势和 感生电动势只是一个 相对的概念。 甲
§8.2 动生电动势 感生电动势 根据磁通量变化的不同原因,把感应电动势 分为两种情况加以讨论。 动生电动势:在稳恒磁场中运动着的导体内产 生的感应电动势。 感生电动势:导体不动,因磁场的变化产生的 感应电动势。 注意:动生电动势和 感生电动势只是一个 相对的概念 。 v

8-2-1 动生电动势 运动导体内电 子受到洛伦兹力的 的作用: F=-e(xB) 非静电场: E=D×B 电动势: 6=fEdl=(o×B)dl
l B A v 8-2-1 动生电动势 运动导体内电 子受到洛伦兹力的 的作用: ( ) FL e B = − v Ii 非静电场: E B k = v 电动势: = = b L a E l B l i k d (v ) d - F
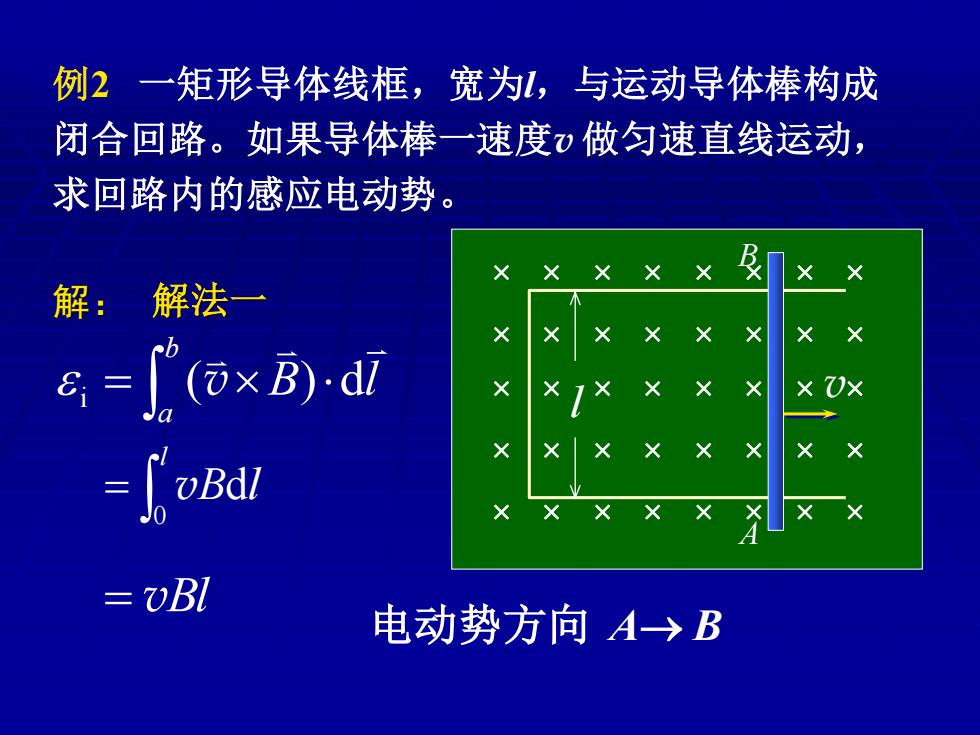
例2一矩形导体线框,宽为,与运动导体棒构成 闭合回路。如果导体棒一速度做匀速直线运动, 求回路内的感应电动势。 解:解法一 e=(×d =foBdi vBl 电动势方向A→B
例2 一矩形导体线框,宽为l,与运动导体棒构成 闭合回路。如果导体棒一速度v 做匀速直线运动, 求回路内的感应电动势。 解: 解法一 = b a B l i (v ) d = l B l 0 v d = vBl 电动势方向 A→ B l B A v