中国科学技术大学：《电磁场理论 Electromagnetic Theory》课程教学资源（课件讲稿）第2章 静电场

§2.2静电场的电位 备注：当电荷分布至无限远时，不可选p。=0。 二、泊松方程和拉普拉斯方程 V2=-p/s 泊松Poisson)方程 特别，若p=0,则 =0 拉普拉斯Laplace)方程 三、泊松方程的形式解与电位表达式 ①泊松方程的形式解

§2.2 静电场的电位 备注：当电荷分布至无限远时，不可选  0   。 二、泊松方程和拉普拉斯方程 0 2     /  泊松(Poisson)方程 特别，若 ρ=0，则 0 2    拉普拉斯(Laplace)方程 三、泊松方程的形式解与电位表达式 ① 泊松方程的形式解

§2.2静电场的电位 第二标量格林定理： "fv器-eis 选：0为待求电位， V2p()=-p(F)180 w-7 ，F∈V,V2w(',)=-6('-) πR3 -4aRa9-as

§2.2 静电场的电位 第二标量格林定理：                V S dS n n ( )dV ( ) 2 2         选：φ 为待求电位， 0 2  (r)  (r)/    r V R    , 4 1   ， ( , ) ( ) 2 r r r r                                                  S V dS n R r n r R r r r dV r R          4 1 ( ) ( ) 4 1 ( ) ( ) ( ) 4 1 0       ρ V S nˆ

§2.2静电场的电位 泊松方程形式解： ) 4Re2-wr} 物理意义与等效思想： 为何称为形式解？ ②电位表达式 V为无限大空间，电荷分布有限空间，选0，=0

§2.2 静电场的电位 泊松方程形式解：                             S V dS n R r n r R dV R r r 1 ( ) 1 ( ) 4 1 ( ) 4 1 ( ) 0           物理意义与等效思想： 为何称为形式解？ ② 电位表达式 V 为无限大空间，电荷分布有限空间，选  0  

§2.2静电场的电位 R 0(= 面电荷分布：p()dW'→p,()dS',, 线电荷分布：p(F)dW'→p,()d',C. 场的远区特性： 零级近似：下=卞-'≈ 0= 零级近似的物理含义：

§2.2 静电场的电位 验证： 0 1 ( ) 1 ( )                          S dS n R r n r R S     时，     V dV R r r ( ) 4 1 ( ) 0      面电荷分布： r dV r dS s ( )   ( )      ，V  S 线电荷分布：     (r)dV   (r)d ，V   场的远区特性： 零级近似：R r r r         ) 1 ( 4 ) 1 ( ) ( 4 1 2 0 2 0 r O r Q r r dV O r V             零级近似的物理含义：

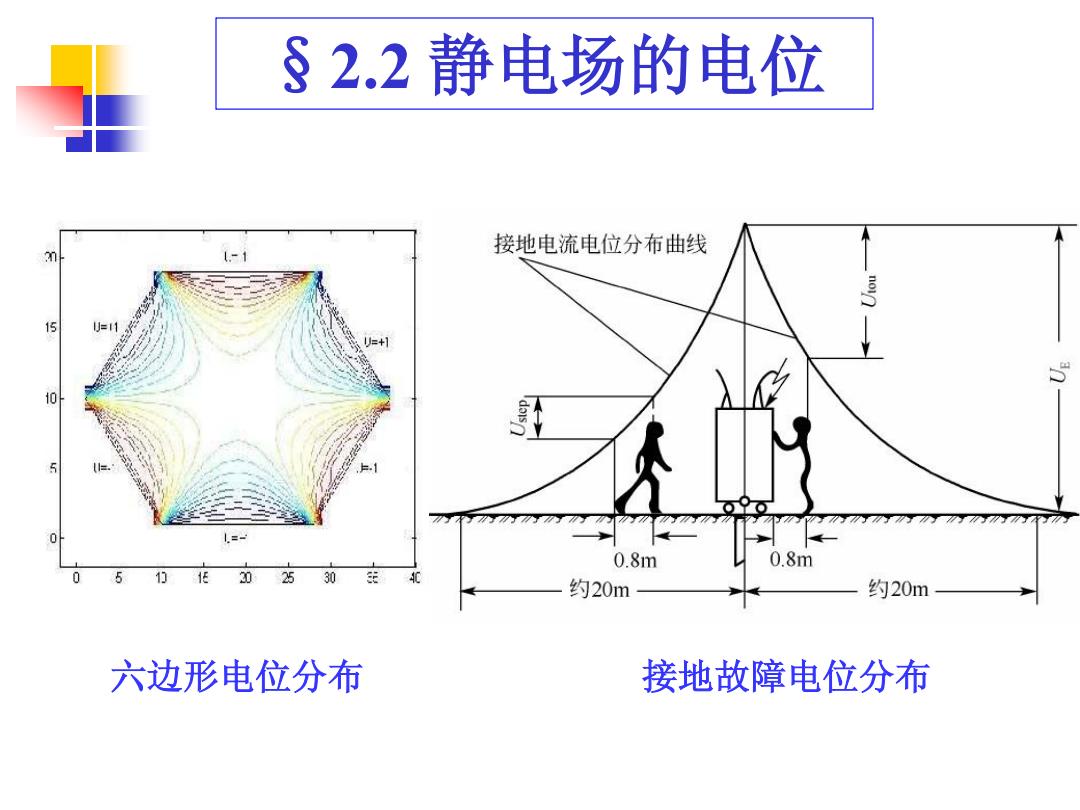
§2.2静电场的电位 接地电流电位分布曲线 10 0.81m 0.8m 1 2025 约20m 约20m 六边形电位分布 接地故障电位分布

§2.2 静电场的电位 六边形电位分布 接地故障电位分布