
§2.1真空中静电场的基本定律 电荷分布在有限区域时,场的远区特性: 远区:下→0或者:卞有限,但'→0 零级近似:F=产-'≈万 E=46 anur+ol=g 零级近似的物理含义:当电荷分布在有限 空间且观察点趋向于无限远时,可以忽略 电荷分布的几何尺寸,将体分布(或面分 布、线分布)的电荷看作一个点电荷
§2.1 真空中静电场的基本定律 电荷分布在有限区域时,场的远区特性: 远区:r 或者:r 有限,但r 0 零级近似:R r r r ) 1 ( 4 ) 1 ( ) ( 4 3 3 0 3 3 0 r O r Qr r r dV O r r E V 零级近似的物理含义:当电荷分布在有限 空间且观察点趋向于无限远时,可以忽略 电荷分布的几何尺寸,将体分布(或面分 布、线分布)的电荷看作一个点电荷

§2.1真空中静电场的基本定律 静电场的基本方程 微分形式: V.E=p/8 静电场的散度方程 V×E=0 静电场的旋度方程 积分形式: fE·=Q/, 静电场的高斯定理 jE·d=0 静电场的环路定理 (Q=pdW为S内的总电荷量) 静电场是无旋场,没有漩涡源,而只有通量源 即电荷分布。电力线从正电荷(或无限远处) 发出,终止于负电荷(或无限远处)。在没有 电荷的区域,电力线是连续的
§2.1 真空中静电场的基本定律 二、静电场的基本方程 微分形式: 0 E / 静电场的散度方程 E 0 静电场的旋度方程 积分形式: 0 E dS Q / S 静电场的高斯定理 0 E d 静电场的环路定理 ( V Q dV 为 S 内的总电荷量) 静电场是无旋场,没有漩涡源,而只有通量源 即电荷分布。电力线从正电荷(或无限远处) 发出,终止于负电荷(或无限远处)。在没有 电荷的区域,电力线是连续的
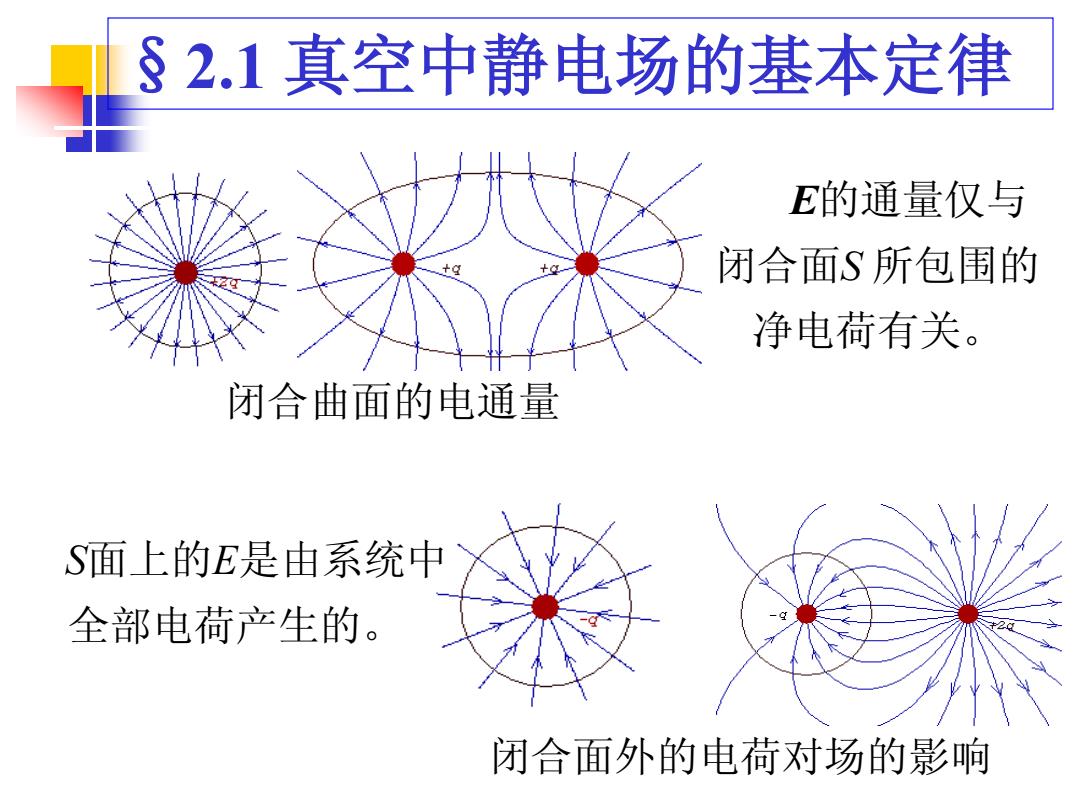
§2.1真空中静电场的基本定律 E的通量仅与 闭合面S所包围的 净电荷有关。 闭合曲面的电通量 S面上的E是由系统中 全部电荷产生的。 闭合面外的电荷对场的影响
闭合曲面的电通量 E的通量仅与 闭合面S 所包围的 净电荷有关。 闭合面外的电荷对场的影响 S面上的E是由系统中 全部电荷产生的。 §2.1 真空中静电场的基本定律

§2.2静电场的电位 静电场的电位表示 静电场为无旋场,因而其电场强度可用 一标量函数的梯度来表示。即: E=-Vo 电位的定义: 任意A和B两点的电位降定义为将单位试验 电荷从A点移到B点电场力所作的功。 A和B两点的电位降=∫E.d0=-∫Vp·d0 ra0d=-∫d0=p-oa p即为电位
§2.2 静电场的电位 一、静电场的电位表示 静电场为无旋场,因而其电场强度可用 一标量函数的梯度来表示。即: E 电位的定义: 任意 A 和 B 两点的电位降定义为将单位试验 电荷从 A 点移到 B 点电场力所作的功。 A 和 B 两点的电位降 B A B A E d d B A A B B A d d φ 即为电位。 A B

§2.2静电场的电位 电位能或势能: 任意A和B两点的电位能减少W4-WB定义为将试验电 荷q从A点移到B点电场力所作的功。即: W4-W。=∫qE.d=q(p4-p8) 性质: 1)电场强度垂直于等位面,且指向电位下降的方向。 2)当电荷分布有限区域时,可选0,=0。此时,任意 点的电位等于将单位试验电荷从该点移至无限远处电 场力所作的功,任意点的电位能或势能为将试验电荷 q从该点移至无限远处电场力所作的功
§2.2 静电场的电位 电位能或势能: 任意 A 和 B 两点的电位能减少 WA-WB定义为将试验电 荷 q 从 A 点移到 B 点电场力所作的功。即: ( ) A B B A WA WB qE d q 性质: 1)电场强度垂直于等位面,且指向电位下降的方向。 2)当电荷分布有限区域时,可选 0 。此时,任意 点的电位等于将单位试验电荷从该点移至无限远处电 场力所作的功,任意点的电位能或势能为将试验电荷 q 从该点移至无限远处电场力所作的功