
第2章热力学第一定律 P4572 2-2热力学第一定律表达式 二存储能 内存储能(内能):U,kJ;=Um,kJ/kg u=(T,V)状态参数 ∮du=0△u=42-4 宏观动能 外存储能 E=>mc 重力位能E,=mg 总存储能卫 E=U+E+E,1,e=u+c12+gz E2-E,=(U2-U)+(E2-E1)+(Ep2-Ep1)
第2章 热力学第一定律 P45~72 2-2热力学第一定律表达式 二.存储能 内存储能(内能):U,kJ;u=U/m,kJ/kg 外存储能 宏观动能 2 2 1 E mc k = 重力位能 E mgz p = 总存储能E E =U + Ek + Ep e = u + c / 2 + gz 2 ( ) ( ) ( ) E2 − E1 = U2 −U1 + Ek 2 − Ek1 + Ep2 − Ep1 u = u(T,v) 状态参数 = 0 ∫ du ∆u = u2 − u1 1kg

第2章热力学第一定律 P4572 2-2热力学第一定律表达式 三流入、流出系统能量 质量具有存储能e=u+c2/2+g 相互 质量传递 质量流动传输能? 作用 能量传递功量、热量
第2章 热力学第一定律 P45~72 2-2热力学第一定律表达式 三.流入、流出系统能量 相互 作用 质量传递 能量传递 功量、热量 质量具有存储能 质量流动传输能 ? e = u + c / 2 + gz 2

第2章热力学第一定律 P4572 23封闭系统能量方程式 封闭系统能量方程式 进入系统的能量-离开系统的能量=系统存储能量的变化 条件:封闭系统 △(-mc2)≈0 △(mgz)≈0 质量具有存储能 相互 质量传递 质量流动传输能 作用 能量传递 功量、热量 E2-E=(U2-U)+(ExzE)+(Ep2=Ep) 方程: 微元 Q=(U2-U)+Wk39=(42-4)+w过程d=d+dw
第2章 热力学第一定律 P45~72 2-3封闭系统能量方程式 一.封闭系统能量方程式 进入系统的能量-离开系统的能量=系统存储能量的变化 相互 作用 质量传递 能量传递 功量、热量 质量具有存储能 质量流动传输能 ( ) ( ) ( ) E2 − E1 = U2 −U1 + Ek 2 − Ek1 + Ep2 − Ep1 条件:封闭系统 ) 0 2 1 ( 2 ∆ mc ≈ ∆(mgz) ≈ 0 方程: Q W ΔU Q = (U2 −U1) +W 1kg q = (u2 − u1) + w δq = du +δw 微元 过程
第2章热力学第一定律 P4572 23封闭系统能量方程式 一封闭系统能量方程式 方程:Q=(U2-U)+WW可以是体积功、拉伸功等 物理意义: 系统从外界吸收的热一部分用于其内能增 加,一部分对外做功 ①单位一致性 注意点: ②功量、热量正负号; ③功量计算 ④任意工质、任意过程 二应用举例 例1.简单可压缩系统,可逆U1=5J,U2=20J
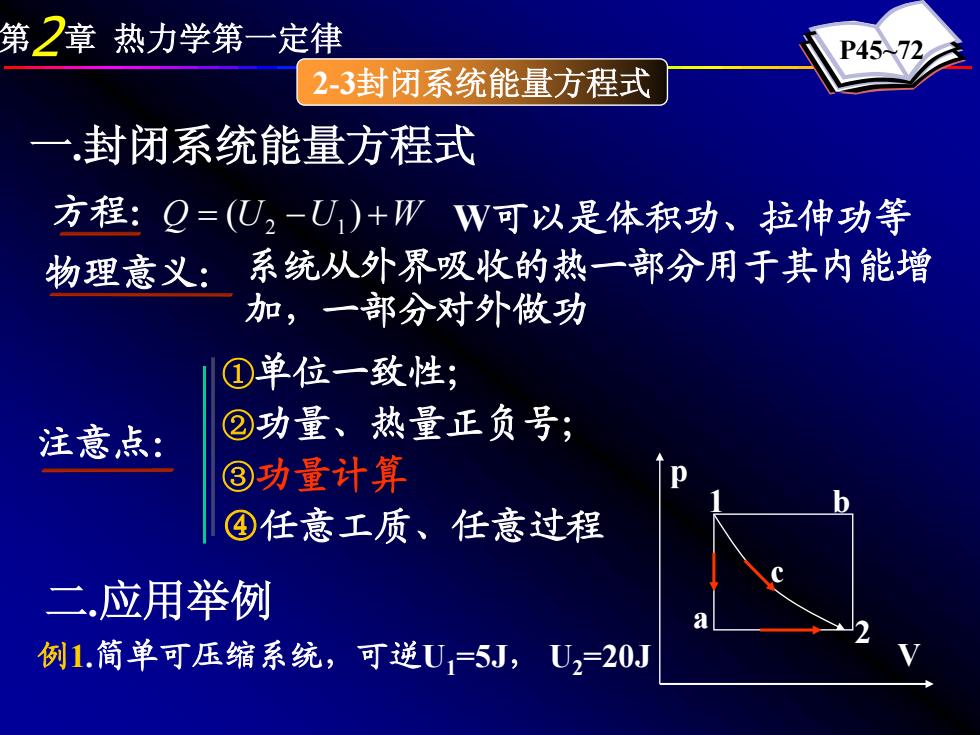
第2章 热力学第一定律 P45~72 2-3封闭系统能量方程式 一.封闭系统能量方程式 方程:Q = (U2 −U1) +W W可以是体积功、拉伸功等 物理意义: 系统从外界吸收的热一部分用于其内能增 加,一部分对外做功 注意点: ①单位一致性; ②功量、热量正负号; ③功量计算 ④任意工质、任意过程 二.应用举例 例1.简单可压缩系统,可逆U1=5J, U2=20J p V 1 2 b a c

第2章热力学第一定律 P45-72 23封闭系统能量方程式 二应用举例 p U1=5J (1)1-c-2,Q=45J,W=30J (2)U=-20J,1-a,W=0J, Q=-25J U2=20J (3)a-2,Q=60J W=20J 注意:①过程的方向,U2-U1;②Q、W正负号 例2.一定量气体在气缸内体积由0.9m3可逆膨胀到1.4m3,过程中, 气体压力保持定值,且p=0.2MPa,若膨胀过程中气体内能增加 了12000J,求:①此过程中气体吸入或放出热量,②若活塞质 量为20kg,且初始时活塞静止,求终态时活塞速度。已知环境压 力po=0.1MPa
第2章 热力学第一定律 P45~72 2-3封闭系统能量方程式 (1)1-c-2,Q=45J,W= p V 1 2 b a c U1=5J U2=20J 30J (2)Ua =-20J,1-a, W= 0J,Q=-25J (3)a-2, Q=60J W=20J 注意: ①过程的方向,U2-U1; ② Q、W正负号 二.应用举例 例2.一定量气体在气缸内体积由0.9m3可逆膨胀到1.4m3,过程中, 气体压力保持定值,且p=0.2MPa,若膨胀过程中气体内能增加 了12000J,求: ①此过程中气体吸入或放出热量; ②若活塞质 量为20kg,且初始时活塞静止,求终态时活塞速度。已知环境压 力p0=0.1MPa