
复习上节课 s=n hv n=为整数。1hv,2hv,3hv 1900年Planck假定: 黑体中的原子分子辐射能量时作简谐振动,它只能发射或吸收频率为ⅴ,数 值为ε=hv的整数倍电磁能,n=为整数。1hv,2hv,3hv 结论:能量量子化
1900年Planck假定: 黑体中的原子分子辐射能量时作简谐振动,它只能发射或吸收频率为ν ,数 值为=hν的整数倍电磁能, n =为整数。 1hν,2hν,3hν = n hν n =为整数。 1hν,2hν,3hν 结论:能量量子化 复习上节课

Ax△px≥h 不确定关系或称不确定原理 适用于电子等微观粒子 不确定关系表明:对于微观粒子不能同 时用确定的位置和确定的动量来描述。 2
2 xpx h 不确定关系表明:对于微观粒子不能同 时用确定的位置和确定的动量来描述。 不确定关系或称不确定原理 适用于电子等微观粒子
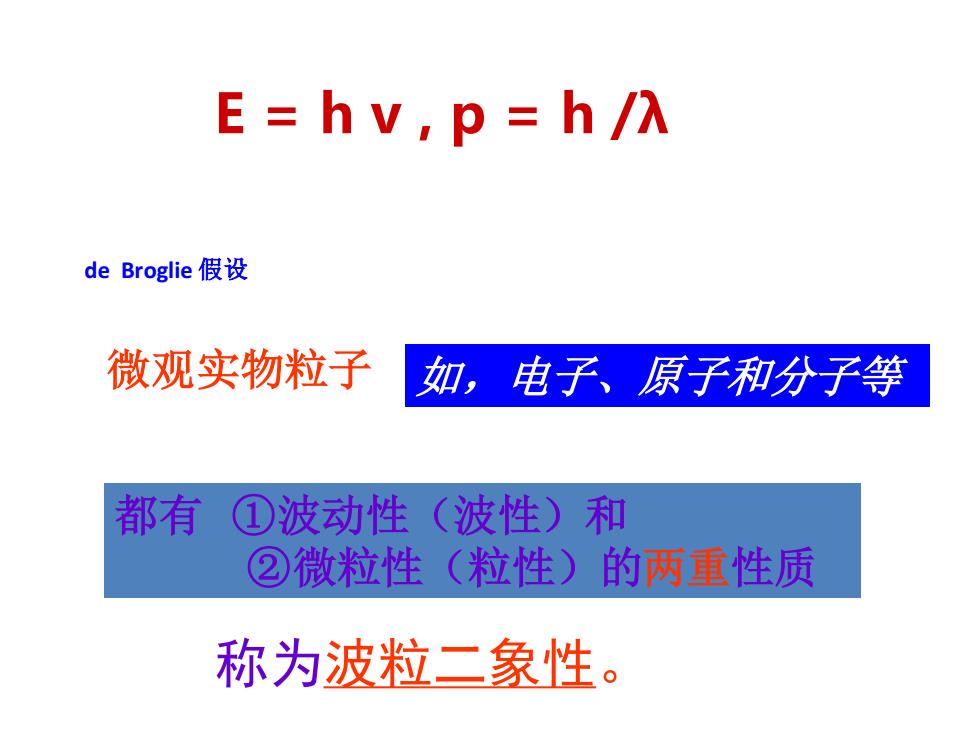
E=hv,p h/A de Broglie假设 微观实物粒子 如,电子、原子和分子等 都有 ①波动性(波性)和 ②微粒性(粒性)的两重性质 称为波粒二象性
E = h v , p = h /λ 称为波粒二象性。 de Broglie 假设 微观实物粒子 如,电子、原子和分子等 都有 ①波动性(波性)和 ②微粒性(粒性)的两重性质

复习上节课 假设3:若某一力学量A的算符[A]作用于某一 状态函数ψ后,等于某一常数a乘以ψ,即 [A]=aΨ 那么对ψ所描述的这个微观体系的状态,其力 学量A具有确定的数值a, a称为力学量算符[A]的本征值, Ψ称为A的本征态或本征波函数, 上式称为A的本征方程
复习上节课 假设3:若某一力学量 A 的算符[A] 作用于某一 状态函数ψ后,等于某一常数 a 乘以ψ,即 [A]ψ= aψ 那么对ψ所描述的这个微观体系的状态,其力 学量 A 具有确定的数值a, a 称为力学量算符 [A] 的本征值, ψ 称为A的本征态或本征波函数, 上式称为A的本征方程
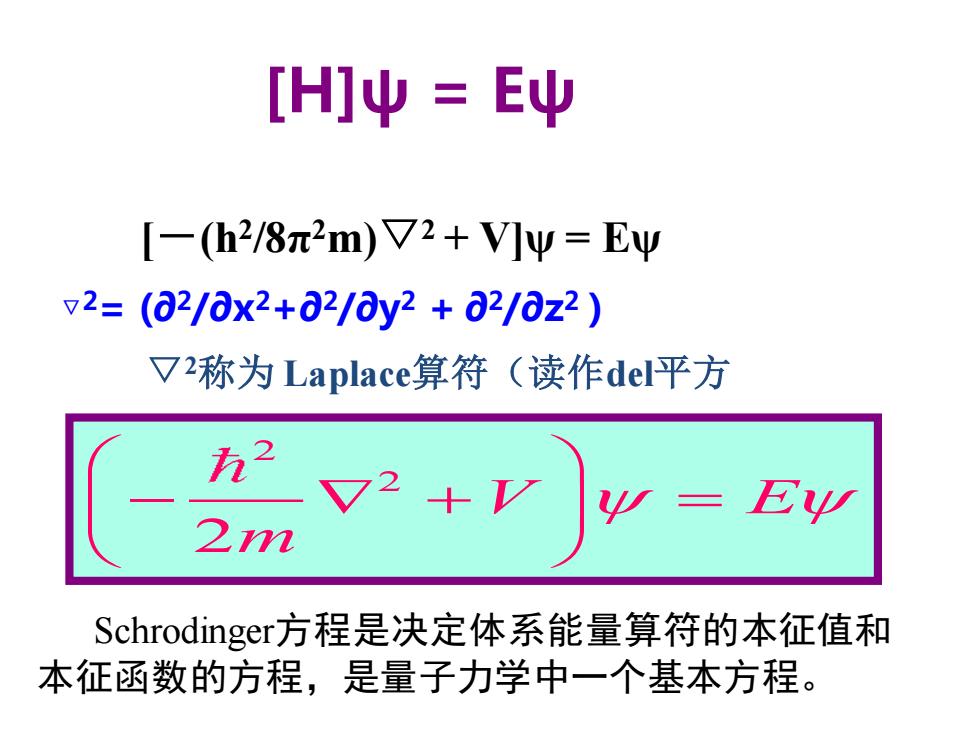
[H]ψ=EΨ [-(h2/8π2m)V2+V]小Ψ=EΨ v2=(a2/ax2+∂2/ay2+a2/az2) V2称为Laplace算符(读作del平方 EΨ Schrodinger方程是决定体系能量算符的本征值和 本征函数的方程,是量子力学中一个基本方程
[-(h2 /8π 2m)▽2 + V]ψ = Eψ [H]ψ = Eψ ▽2= (∂2/∂x 2+∂2/∂y 2 + ∂2/∂z 2 ) ▽2称为 Laplace算符(读作del平方 2 2 2 V E m − + = Schrodinger方程是决定体系能量算符的本征值和 本征函数的方程,是量子力学中一个基本方程