
ther Typeo 3.2.2Thermodynam olution 霾想溶液的热力学 稀溶液的许多性质, -k(N,Inm+N Inn LS≠-k(Nln+N,nm (1)Flory-Hugginsi高分子溶液理论 推导中的假设: ·on-luggins底分子液理论 ·①中分于的排列象品体一样,是品格列年个海相分子占一个格子 ②高分子酰是柔性的,所有构象只有相问的能 是匀分布的得段古有任意一个子的几 部的 用统计热力学的方法推导出 Entropy混合桶 AS= AS=-R(n,Ino.+lng, △S=-(Nn乃+N,n) △H.=RT%mg2 AF=RT(n Ing+n:Ing:+m 由于有众多打 高 Enthalpy混合格 化学位:△4,=RT[n+-+ △4=RTx-,p 的通意文一个剂分子从溶剂中到筒高分子中的能
Other Types of Solutions 其它类型溶液 ( ln ln ) 1 1 2 2 S k N n N n M ( ln ln ) N1 n1 N2 n2 SM k HM ≠ 0 Athermal solutions 无热溶液 Regular solution 正规溶液 Irregular solution 无规溶液 HM = 0 ( ln ln ) N1 n1 N2 n2 SM k HM ≠ 0 不能外传 ( l N1 0 外传 不能外传egul 正 外传规溶液 外传 不能 ution 能外传 不 l N2 不能 Ty S k( M k( HM ≠ 0 solution 液 H 高分子溶液是真溶液,是热力学稳定的体系,溶 液的性质不随时间而变化,因此,我们可以用热力学 方法研究高分子稀溶液,用热力学函数来描述高分子 稀溶液的许多性质。 3.2.2 Thermodynamics of ideal solution 理想溶液的热力学 不能外传 来描 传 外传 不能外传 溶 传 液 传的 传 不能外传 液 不能是 不能真 不能溶 随时不间 不能外传 力 溶 学不能 不能 s of 力学 此,我们 用热力学函数来 Flory-Huggins高分子溶液理论 Flory和Huggins从液体的似晶格模型出发,用统计热 力学的方法,推导出了高分子溶液的混合熵,混合热和混 合自由能的关系式。 (1)Flory-Huggins高分子溶液理论 不能外传 外传 不能外传 不能外传 s高 能外分 能外传子 Huggin 推不导 不能外传 用不能统计 热 不能 高 晶格 子溶液的混 推导中的假设: ①溶液中分子的排列象晶体一样,是晶格排列。每个溶剂分子占一个格子, 每个高分子占有相连的 x 个格子,x 个 高分子与溶剂分子的体积比(高分 子由 x 个链段组成)每个链段与溶剂分子的体积相等,每个链段只占一个 格子 ②高分子链是柔性的,所有构象具有相同的能量 ③所有高分子链具有相同的聚合度 ④溶液中高分子链段是均匀分布的(即链段占有任意一个格子的几率相等) 不能外传 的 传外 能 外传量 外传 ( 不 即 不能链 不能段 外传 不能外传 子链 传是 传柔 所有 能外高 能外传分子 ④ 不能溶 不能外液中 不能外传 象 能 晶 能外体 能外一 连 不的 不能x 个 成)不每 不能外传 剂 不能分 不能外子占 分子 不能的体 每 不 不能 个 高 剂分子的体 构象具有相同的 同的聚合度 段是均匀分布的 Flory-Huggins运用统计热力学的方法推导出 的高分子溶液的混合熵: ( ln ln ) 1 1 2 2 S R n n m 1 1 2 H RT n m ( ln ln ) 1 1 2 2 1 1 2 F RT n n n m 式中: 为Huggins相互作用参数,是一个表征 溶剂分子与高分子相互作用程度大小的参数。 1 不能外传2 ln2 互 不 作 不用 不能参 用不程 外传 不能外传Fm 能外式 不能外传 合熵 传 ( ln 1 R n RT 不能外传 不能 力学 ln l 1 1 2 n 为Huggins相互作 子与高分子相互 Entropy 混合熵 ( ln ln ) 1 1 2 2 S k N v N v M 1 2 1 1 N xN N v 1 2 2 2 N xN xN v ( ln ln ) 1 1 2 2 S k N n N n M Mole fraction Solvent1 Polymer Volume fraction N1个溶剂分子与N2个高分子的混合熵 > N1个溶剂分子与N2个小分子的混合熵 N1个溶剂分子与N2个高分子的混合熵 < N1个溶剂分子与xN2个小分子的混合熵 solvent 2 Solvent 注:推导步骤与理想溶液相近,但根据高分子的特点,在计算排列方式时,除了考虑高分子之 间的排列外,还要考虑一个高分子内链段的排列,而且后一个链段的位置必然受到前一个 链段的牵制。另外,由于有众多的构象,纯高分子的熵不等于0。 不能外传1 N x 剂 能 分 能外子 能外与 能外N 个 个溶 不剂 不能分 不能子与 的不特 外传众 传 多 传的 传 不能外传1 外 个 外 溶 外传剂 外传分 外传子 N 能1 不能个 能外溶 能外剂 不能注: 不能外传 ( ln N1 不能外传vent 不能外传 action 不能 n 2 v 2 N e fraction v 的混合熵 > N1个溶剂分 分子的混合熵 < N1个溶 溶液相近,但根据高 还要考虑一个高分 制。另外,由于有众 Enthalpy 混合焓 1 2 1 1 2 H (Z 2)N v kT N v M kT Z kT Z ( 2) 1 Flory-Huggins interaction parameter Flory-Huggins 相互作用参数(Huggins参数) 1kT 的物理意义:一个溶剂分子从纯溶剂中拿到纯高分子中引起的能量变化 1 2 1 2 H M Z (N N )n n Mole fraction Solvent1 solvent 2 Volume fraction (v1=1) 不能外传 Z 不能外传g 传 g 传in 传 外传 不能外传 不能外传1 2)N ns 传外 不能外传ction 不能 H kT Z ( 2) n parame 用参数(Hugg 意义:一个溶剂分子 on (v1 ) ] 1 [ln (1 2 1 1 2 1 2 x RT 可分解为两项,第一项相当于理想溶液的化学位变化, 第二项相当于非理想部分,称为“过量化学位”(又称 “过剩”、“超额”)。 化学位: 1 2 1 2 ) 2 1 RT( E 1 = 可见 1 =1/2, 即 =0时才符合理想溶液的条 件,此状态称为 状态。当 <1/2 即 < 0, 溶解自发发生。 < 0。 E 1 1 E 1 不能外传2 2 ) 2 ) 时 不能才 不能外符合 <1 外传 不能外传 可 能外见 件能外 不溶 不能外传 T , 能第 能外传一项 理 不能想 不能外部分 超额不能” 不能外传] 变 能 化 能外, 又 不称 不能 不能 过量 1 1 RT( 即 =0时 为 状态。当 生。 < 0 E 1 E 1 状
Flory-Krigbaum稀溶液理论 在前而理论的基础上FKiham又提出了稀望 城通论。以立服由于似品格烘型没有考康到稀激液的高分 ®来考虑溶质分子与剂分子的相互作用 液中原来不可能实现的构象有可能实现 3.2.2 Thermodynamics of idealsotio 理想溶液的热力学 摘△Sy=-k(N,nm+N2lnm,) 格△Hw=0 直由能△Gu=kT(N,lnn+N,lnn, 、=RT Inm 0-1 SA- RT Inn 3.2.3 Thermodynamics of regular solutior 正规溶液的然力 甲AZB 甲B乙A Regular solution ASAS AH0 AA+8-8→2A-8 A一时的量为 AHy =Ni-Ae e-2+2头-2W+m △SM=-kNnm+N,nm) △H=Z△c-(N1+N2mm 高分于涂旅与理想缘液的偏是 自由能AGw-Z△N+N:nm:+kr(N,n%+N:lnm 。高分子的体积比溶剂分子大得多 ·混合热不等于0 化学位△4=RTnm+N,Z△an ·混合箱比理想溶液大 过量化拳位A4=A4-A=N,Z△a Flory-Huggin
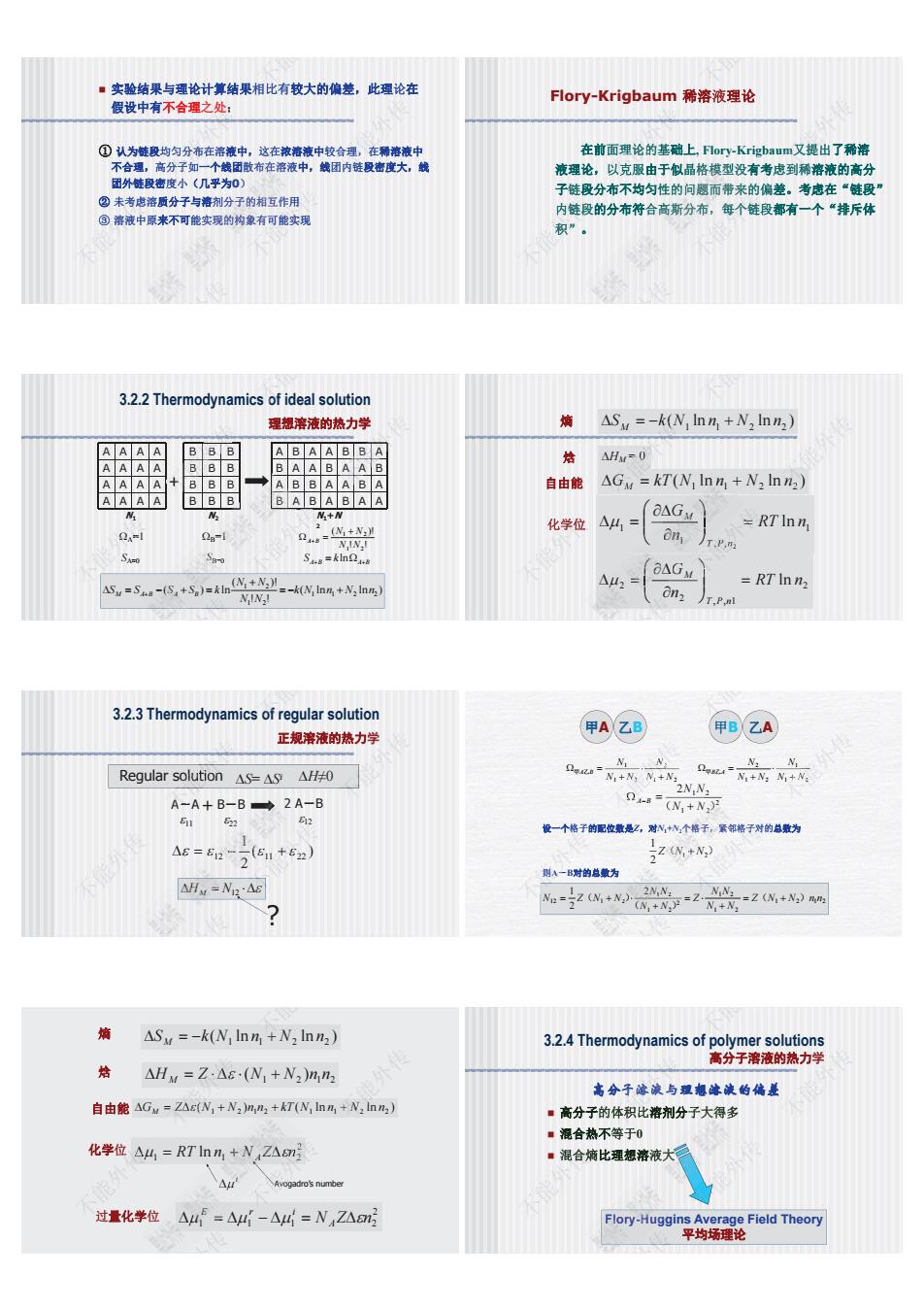
实验结果与理论计算结果相比有较大的偏差,此理论在 假设中有不合理之处: ① 认为链段均匀分布在溶液中,这在浓溶液中较合理,在稀溶液中 不合理,高分子如一个线团散布在溶液中,线团内链段密度大,线 团外链段密度小(几乎为0) ② 未考虑溶质分子与溶剂分子的相互作用 ③ 溶液中原来不可能实现的构象有可能实现 不能外传 作用 传 可 外传 能能 能外实 能外传现 外传 不能外传 未考 传虑 ③ 传外 溶 外传液 外传中 不能外传处 传: 传 匀 不能分 不能外布在 高分不能子如 小 不能外传 合 不 理 不能, 不能在 内不链 不能 比 这在 散布在溶液 0) 剂分子的相互作用 能实现的构象有可 在前面理论的基础上, Flory-Krigbaum又提出了稀溶 液理论,以克服由于似晶格模型没有考虑到稀溶液的高分 子链段分布不均匀性的问题而带来的偏差。考虑在“链段” 内链段的分布符合高斯分布,每个链段都有一个“排斥体 积”。 Flory-Krigbaum 稀溶液理论 不能外传 来 传 的 每 传外个 外传链 外传段 外传 不能外传内 外传链 外传段 积 能外传” 不能外传 面理 不能论 不能外的 以克不服 不能外传 m又 不能提 不能出 到不稀 不能 晶格模型 的问题而带来 合高斯分布,每 3.2.2 Thermodynamics of ideal solution 理想溶液的热力学 AAAA AAAA AAAA AAAA BBB BBB BBB BBB ABAABBA BAABAAB ABBAABA BABABAA + N1 N2 N1+N 2 ! ! ( )! 1 2 1 2 N N N N A B A B A B S k ln A=1 B=1 SA=0 SB=0 ( ln ln ) ! ! ( )! ( ) ln 1 1 2 2 1 2 1 2 k N n N n N N N N S S S S k M A B A B 不能外传N 不 外传 不能外传N1 A=1 不 不能外传 B B B B + B 不能外传 B A外 A A A 不能 s of A B A B=1 SB=0 (S S ) k B S A S B ( ln ln ) 1 1 2 2 S k N n N n M ( ln ln ) N1 n1 N2 n2 GM kT 1 , , 1 1 ln 2 RT n n G T P n M HM = 0 2 , , 1 2 2 RT ln n n G T P n M 熵 焓 自由能 化学位 不能外传 , , 2 R T P n 不能 外传 不能外传 化学 外传位 外传 不能外传( G 不能外 M 0 不能外传 n ) 不能 ln n1 1 n G T M 2 G 3.2.3 Thermodynamics of regular solution 正规溶液的热力学 + 11 HM N12 A-A B-B 2 A-B 22 12 ( ) 2 1 12 11 22 ? Regular solution S= Si H≠0 不能外传 12 ) 11 2 外传 不能外传 不能外传 A- olutio 不能外传 不能of r HM N1 2 22 ( 2 1 12 1 1 2 2 1 2 1 N N N N N N A B 甲 乙 1 2 1 1 2 2 N N N N N N B A 甲 乙 甲A 乙B 甲B 乙A 2 1 2 2 1 2 (N N ) N N A B 设一个格子的配位数是Z,对N1+N2个格子,紧邻格子对的总数为 ( 1 2 ) 2 1 Z N N 则A-B对的总数为 1 2 1 2 1 2 1 2 2 1 2 1 2 12 1 2 2 2 1 Z N N n n N N N N Z N N N N N Z N N ( ) ( ) ( ) 不能外传 格子对 不 外传 不能外传 则 不能外A 能外 不 不能外传 2 N N N 不能外传 N2 不能 2 2 2 N ) +N2个格子,紧邻格 ( 1 2 ) 2 Z N1 N2 1 1 2 1 2 2 N1 N N1N2 N1 N2 ( ) ( ln ln ) 1 1 2 2 S k N n N n M ( ) ( ln ln ) 1 2 1 2 N1 n1 N2 n2 GM Z N N n n kT 2 1 1 2 RT ln n NAZn 熵 焓 自由能 化学位 1 2 1 2 H Z (N N )n n M 过量化学位 2 1 1 1 2 N Z n A E r i i Avogadro’s number 不能外传2 n2 不 Avog 不能 外传 不能外传 位 传 不能外传 Z能外传 (N Z 不能外传 N l 不能 2 n1 NAZn 位 1 E i 3.2.4 Thermodynamics of polymer solutions 高分子溶液的热力学 高分子溶液与理想溶液的偏差 高分子的体积比溶剂分子大得多 混合热不等于0 混合熵比理想溶液大 Flory-Huggins Average Field Theory 平均场理论 不能外传 不能 外传 不能外传混 传 合 传熵 传 不能外传 子 能 溶 能外液与 的 不 体 不积 不能比 等 不能外传 学 传 不能 p 子大得 液大 Flory-Hugg