
标准偏差与平均偏差 。当≥20时,标准偏差与平均偏差的关系: δ=0.7979o≈0.80o 平均值的标准偏差 。从总体中抽出一组容量为的样本x1,x2,.,xm O n ·对于有限次 或:d,=
⚫ 标准偏差与平均偏差 ⚫ 当n20时,标准偏差与平均偏差的关系: = 0.7979 0.80 n x = n x = ⚫ 平均值的标准偏差 ⚫ 从总体中抽出一组容量为n的样本x1,x2,.,xn ⚫ 对于有限次 n s sx = n d 或:dx =
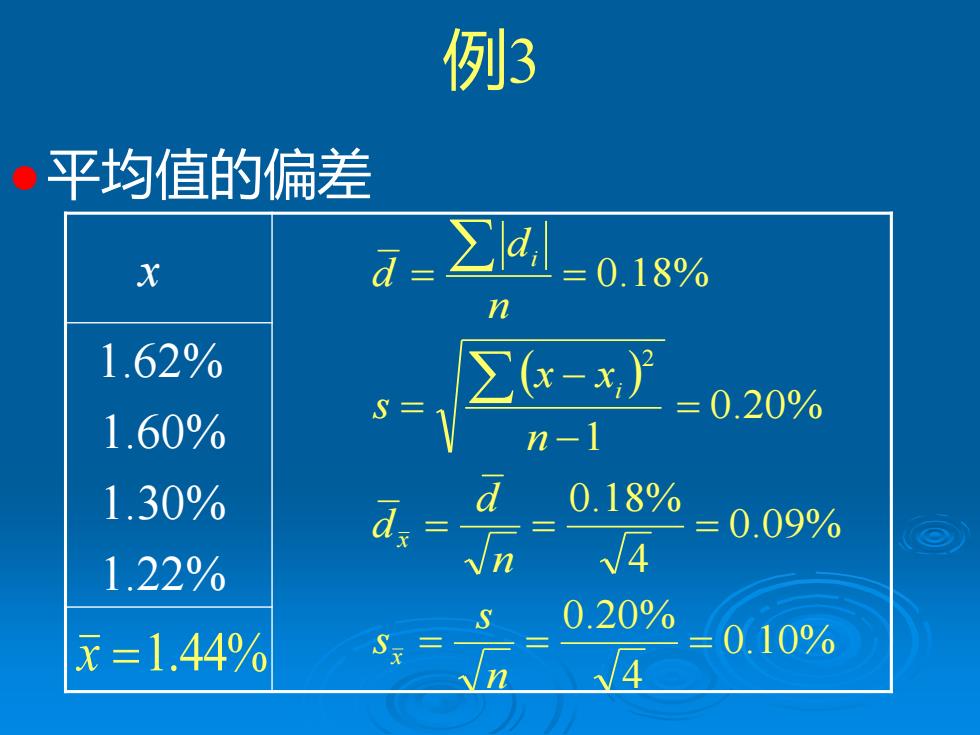
例3 ·平均值的偏差 X a=∑ 1=0.18% n 1.62% ∑(-x尸 =0.20% 1.60% n-1 1.30% d 0.18% d; =0.09% 1.22% 0.20% x=1.44% S,三 三 0.10%
例3 ⚫平均值的偏差 x 1.62% 1.60% 1.30% 1.22% x =1.44% ( ) 0.10% 4 0.20% 0.09% 4 0.18% 0.20% 1 0.18% 2 = = = = = = = − − = = = n s s n d d n x x s n d d x x i i

§7-2 随机误差的正态分布 我们在第一章中学过,误差根据误差的性质和产生的 原因,可分为系统误差和随机误差。 系统误差(可测误差):是由某种固定的原因所造成 的。 特征:恒定性 重复测定重复出现 单向性 误差的大小、方向、正负一定 可测性 可以测定与校正 产生的原因:由一些经常性的比较固定原因造成的
§7-2 随机误差的正态分布 ⚫ 我们在第一章中学过,误差根据误差的性质和产生的 原因,可分为系统误差和随机误差。 ⚫ 系统误差 (可测误差):是由某种固定的原因所造成 的。 ▲ 特征:恒定性——重复测定重复出现 单向性——误差的大小、方向、正负一定 可测性——可以测定与校正 ▲ 产生的原因:由一些经常性的比较固定原因造成的

偶然误差(「 随机误差) 产生的原因:由一些不确定的偶然因素所引 起。 ▲特征:不恒定,可大可小,时正时负,难以 预料和控制。 随机误差似乎没有什么规律,但在同一条件下 进行多次(大量)测定,则随机误差的分布符 合统计规律。即按“正态分布”规律分布
偶然误差 (随机误差) ▲ 产生的原因:由一些不确定的偶然因素所引 起。 ▲ 特征:不恒定,可大可小,时正时负,难以 预料和 控制。 随机误差似乎没有什么规律,但在同一条件下 进行多次(大量)测定,则随机误差的分布符 合统计规律。即按“正态分布”规律分布

一、 正态分布 ·正态分布即所谓的高斯分布,它的曲 线呈对称钟形,两头小,中间大,分 布曲线有最高点。 0 xX-四
一、正态分布 ⚫正态分布即所谓的高斯分布,它的曲 线呈对称钟形,两头小,中间大,分 布曲线有最高点。 y 1 x x- 0