例如: 测定铁矿石中铁含量8次,数据如下: 56.12、56.30、 56.32、56.38、56.34、 56.40、56.42、 56.50。 平均值为56.35 按平均偏差结课,会使所得偏差结果偏小 这样大偏差得不到充分的反映。 如果把数学的统计方法来处理精密度,这 样大偏差就能得到充分的反映,即用“标准 偏差”表示。在分析化学中广泛采用”标准 偏差”来衡量数据的分散程度
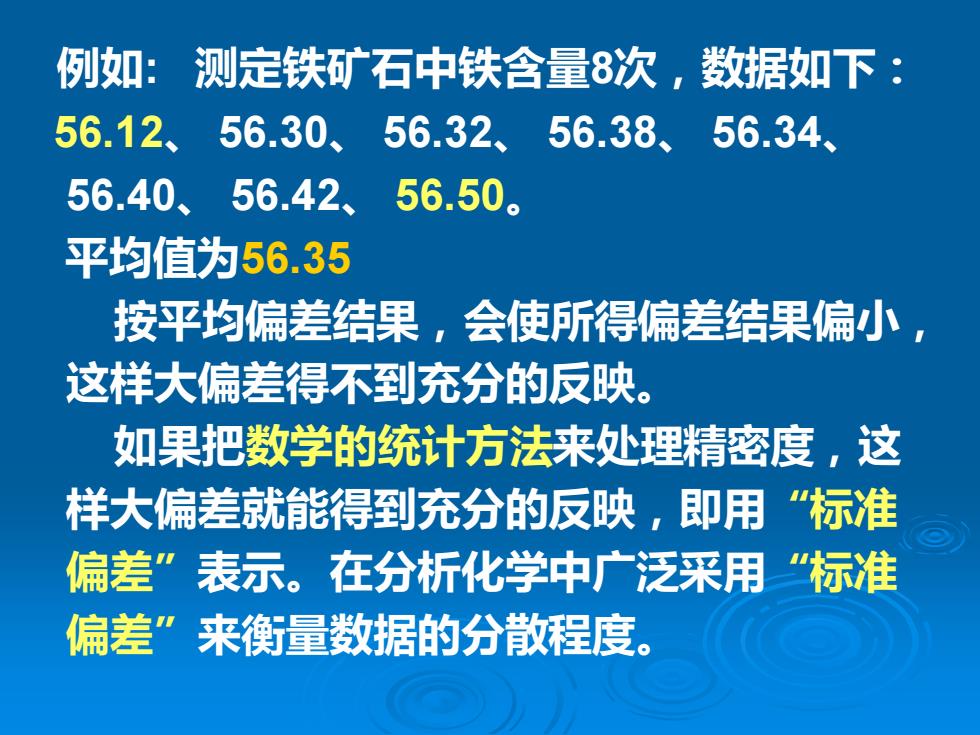
例如: 测定铁矿石中铁含量8次,数据如下: 56.12、 56.30、 56.32、 56.38、 56.34、 56.40、 56.42、 56.50。 平均值为56.35 按平均偏差结果,会使所得偏差结果偏小, 这样大偏差得不到充分的反映。 如果把数学的统计方法来处理精密度,这 样大偏差就能得到充分的反映,即用“标准 偏差”表示。在分析化学中广泛采用“标准 偏差”来衡量数据的分散程度

§7-1标准偏差 总体标准偏差σ:(读“西格玛”) 。趋于无限次时,各测量值对总体平均 值的偏离,用总体标准偏差o表示。 ∑- n ·大小偏差都能得到充分的反映,很好说 明数据的分散程度
§7-1 标准偏差 ⚫总体标准偏差: (读“西格玛”) ⚫ n趋于无限次时,各测量值对总体平均 值的偏离,用总体标准偏差表示 。 n x i − = 2 ( ) ⚫ 大小偏差都能得到充分的反映,很好说 明数据的分散程度

● 样本标准偏差s: f尺n-l, ∑- 自由度 。为有限次时, S1 n-1 ·相对标准偏差RSD或变异系数CV: RSD=二×100% X
⚫样本标准偏差s: ⚫ n为有限次时, 1 ( ) 2 − − = n x x s i f=n-1, 自由度 ⚫相对标准偏差RSD或变异系数CV : = 100% x s RSD

例1 某样测定结果分析见下表 x d d? 2d, 0.036% n 10.48% 0.05% 2.5×10-7 d 10.37% 0.06% 3.6×10-7 d ×100%=0.35% 10.47% 0.04% 1.6×10-7 10.43% 0.00% 0 S= =0.046% 10.40% n-1 0.03% 0.9×10-7 k=10.43%∑d=0.18%∑f=8.6×10 RSD ×100%=0.44%
例1 ⚫某样测定结果分析见下表 x di 2 10.48% 10.37% 10.47% 10.43% 10.40% 0.05% 0.06% 0.04% 0.00% 0.03% 2.5×10-7 3.6×10-7 1.6×10-7 0 0.9×10-7 x = 10.43% di di = 0.18% 2 7 di 8.6 10− = 100% 0.44% 0.046% 1 100% 0.35% 0.036% 2 = = = − = = = = = x s RSD n d s x d d n d d i r i
例2 两组数据比较 X d s +0.3,-0.2,-0.4,+0.2,+0.1, 0.24 0.28 +0.4,0.0,-0.3,+0.2,-0.3 0.0,+0.1,-0.7,+0.2,-0.1 -0.2,+0.5,-0.2,+0.3,+0.1 0.24 0.33 两组数据的平均偏差均为0.24,两组数据的分散程 度无法区分开来,而标准偏差值不同,所以,用标 准偏差衡量数据的分散程度比平均偏差更为恰当
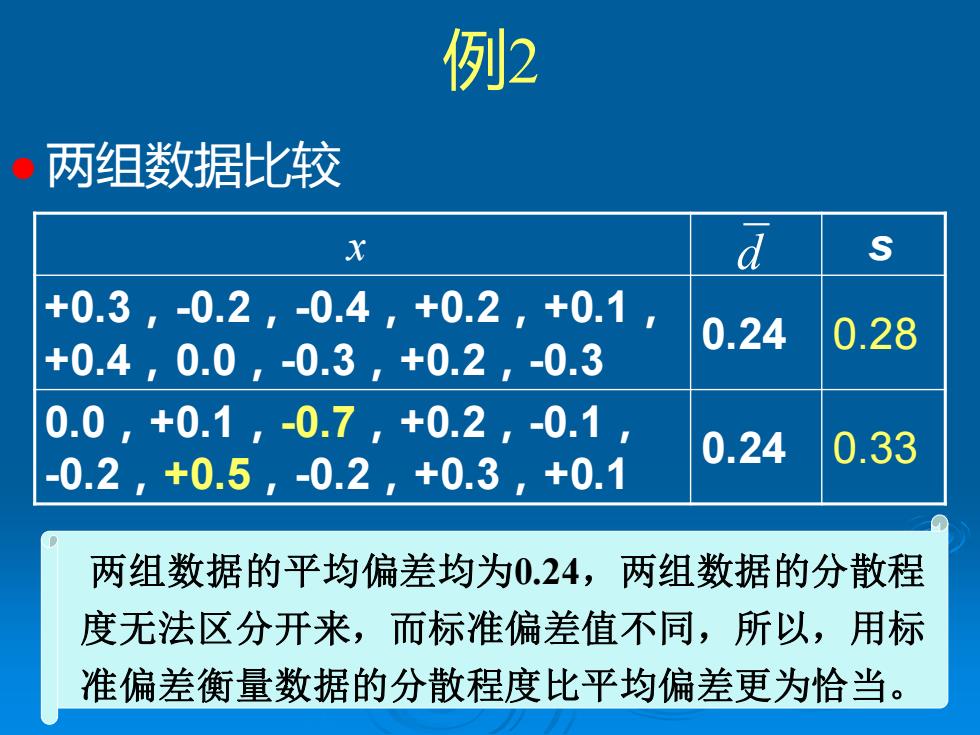
例2 ⚫ 两组数据比较 x s +0.3,-0.2,-0.4,+0.2,+0.1, +0.4,0.0,-0.3,+0.2,-0.3 0.24 0.28 0.0,+0.1,-0.7,+0.2,-0.1, -0.2,+0.5,-0.2,+0.3,+0.1 0.24 0.33 d 两组数据的平均偏差均为0.24,两组数据的分散程 度无法区分开来,而标准偏差值不同,所以,用标 准偏差衡量数据的分散程度比平均偏差更为恰当