
L.=m,0,=m,r0 刚体对Oz轴的角动量为 L.=∑L.-∑mrio=(mro 令 .=Σy 单位:kgm2 J为刚体对Oz轴的转动惯量。 L2=J20
i i i = m r v 2 i i = m r Liz 刚体对Oz轴的角动量为 = = = i i i i i i i z i z L L m r ( m r ) 2 2 令 = i z i i J m r 2 J z 为刚体对 Oz 轴的转动惯量。 Lz = J z 2 单位: kgm

结论:刚体的转动惯量与刚体的形状、大小、质量 的分布以及转轴的位置有关。 对于质量连续分布的刚体: J=fr'dm=f,plr J=fdm=[y"ars (面质量分布) J=Jy"dm=Sr"ndi (线质量分布)
刚体的转动惯量与刚体的形状、大小、质量 的分布以及转轴的位置有关。 结论: 对于质量连续分布的刚体: = = V V J r dm r dV 2 2 = = S S J r dm r dS 2 2 (面质量分布) = = L L J r dm r dl 2 2 (线质量分布)

例1计算质量为m,长为l的细棒绕一端的转动惯量。 解:J=∫r2dm dn=pds=%d dm r2=x2 -s-m
例1 计算质量为m,长为l 的细棒绕一端的转动惯量。 o x z J r dm 2 解: = x l m dm = dx = d 2 2 r = x l l x l m x l m J x 0 3 0 2 3 1 = d = 2 3 1 J = ml dx dm x O

例2一质量为m,半径为R的均匀圆盘,求对通过盘 中心并与盘面垂直的轴的转动惯量。 解: dm=o2元rdr J=∫r2dm=2mo∫rd J=2πordn πoR=1 2-2
o R 例2 一质量为m,半径为R的均匀圆盘,求对通过盘 中心并与盘面垂直的轴的转动惯量。 解: dm = 2π rdr J = r dm 2 = 2π r dr 3 = R J r r 0 3 2π d 2 4 2 1 2 π mR R = = r dr
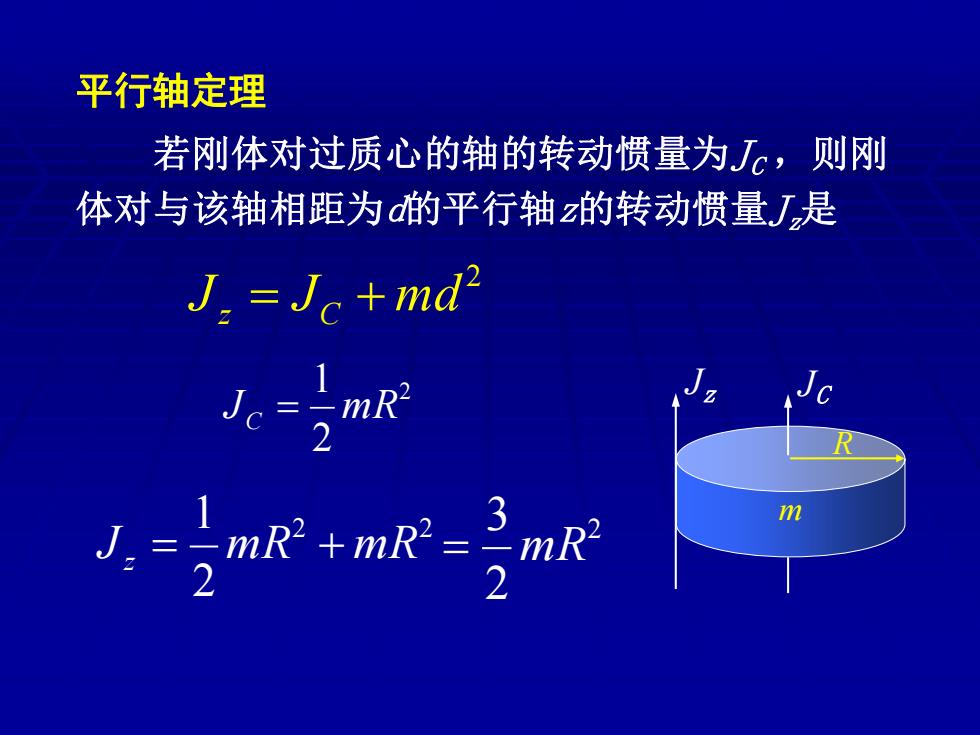
平行轴定理 若刚体对过质心的轴的转动惯量为J,则刚 体对与该轴相距为d的平行轴z的转动惯量J是 J.=Jc+md2 .-mR'+m-3mk
m R Jz 平行轴定理 若刚体对过质心的轴的转动惯量为JC ,则刚 体对与该轴相距为d的平行轴z的转动惯量Jz是 2 J J md z = C + 2 JC 2 1 JC = mR 2 2 2 1 Jz = mR + mR 2 2 3 = mR