非常满意 300 3000 合计 3000 中位数位置=3000/2=1500 从学生数累计看,中位数在第三组,所以,Me=一般。 [例3-5]有8名工人,每人日产零件数按从低到高的顺序排列如下:17、19、20、22、23、23、 24、25(件人)。则 M.-+5)=22+23)=25 中位数为22.5件人,这个数字反映了工人总体日产零件数的一般水平。 (2)由单项式分组数量数据确定中位数。单项式数量数据分组已经将数据顺序化,这时数据个数 即总体单位数刀=Σ人确定中位数位置的方法要通过累计次数计算。 [例36]由表3-5数据计算中位数。 表3-5 教师开课门数累计频数表 开课门数x 教师数f 向上累计数(人) 向下累计数(人) 1 15 85 2 30 45 70 3 28 73 40 4 12 12 合计 85 中位数的位置是85/2=42.5,因此,Me=2。 (3)由组距式分组的数量数据确定中位数。组距式分组的数量数据也已经将数据顺序化,确定中 位数的方法与单项式分组数据一样,先通过累计次数确定中位数所在的组,再确定中位数,只是,这时 的中位组的变量值是非唯一的 一段区间,在假定中位数组内的各数据均匀分布的前提下,利用下 面的公式: 算中位数的近似值 下限公式: ∑f M。=Lw,+ -SM (3-7) fs, 上限公式: ∑f -S M。=Uy,- -xdM. (3-8) JM, 式中:M,表示中位数:L,表示中位数所在组的下限:U表示中位数所在组的上限:S,表 示向上累计至中位数所在组前一组的次数:S,1表示向下累计至中位数所在组后一组的次数:厂,表 6
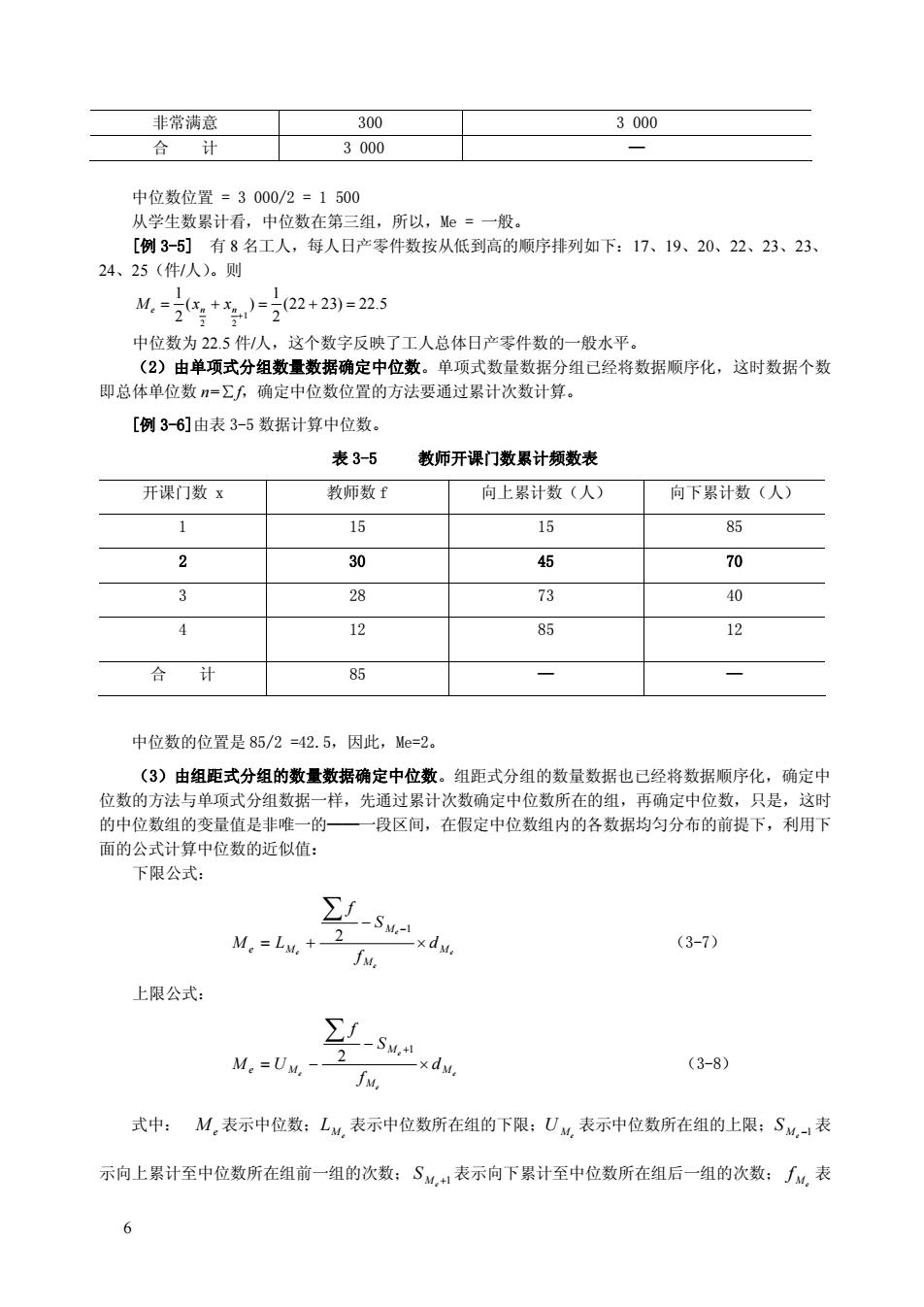
6 非常满意 300 3 000 合 计 3 000 — 中位数位置 = 3 000/2 = 1 500 从学生数累计看,中位数在第三组,所以,Me = 一般。 [例 3-5] 有 8 名工人,每人日产零件数按从低到高的顺序排列如下:17、19、20、22、23、23、 24、25(件/人) 。则 1 2 2 1 1 ( ) (22 23) 22.5 2 2 Me n n x x + = + = + = 中位数为 22.5 件/人,这个数字反映了工人总体日产零件数的一般水平。 (2)由单项式分组数量数据确定中位数。单项式数量数据分组已经将数据顺序化,这时数据个数 即总体单位数 n=∑f,确定中位数位置的方法要通过累计次数计算。 [例 3-6]由表 3-5 数据计算中位数。 表 3-5 教师开课门数累计频数表 开课门数 x 教师数 f 向上累计数(人) 向下累计数(人) 1 15 15 85 2 30 45 70 3 28 73 40 4 12 85 12 合 计 85 — — 中位数的位置是 85/2 =42.5,因此,Me=2。 (3)由组距式分组的数量数据确定中位数。组距式分组的数量数据也已经将数据顺序化,确定中 位数的方法与单项式分组数据一样,先通过累计次数确定中位数所在的组,再确定中位数,只是,这时 的中位数组的变量值是非唯一的——一段区间,在假定中位数组内的各数据均匀分布的前提下,利用下 面的公式计算中位数的近似值: 下限公式: e e e e M M M e M d f S f M L ¥ - = + - Â 1 2 (3-7) 上限公式: e e e e M M M e M d f S f M U ¥ - = - + Â 1 2 (3-8) 式中: M e 表示中位数; M e L 表示中位数所在组的下限; M e U 表示中位数所在组的上限; -1 M e S 表 示向上累计至中位数所在组前一组的次数; +1 M e S 表示向下累计至中位数所在组后一组的次数; M e f 表

示中位数所在组的次数:d,表示中位数所在组的组距。 [例3-7刀根据表3-6数据,计算农民家庭年人均纯收入中位数。 表3-6农民家庭年人均纯收入累计次数表 年人均纯收入(元) 农民家庭数(户) 向上累计户数 向下累计户数 1000-1200 240 240 3000 12001400 480 720 2760 1400~1600 105 170 2280 1600-1800 600 2370 1230 1800~2000 270 2640 630 2000-2200 2850 360 2200-2400 120 2970 150 2400~2600 30 3000 30 合计 3000 3000-720 -×dk=1400+ 1050 ×200=1548.57(元) -5d-60-2 00-1230 M,=U,-2 050 ×200=1548.57(元) 计算表明,这3000户农民家庭年人均纯收入的中位数是1548.57元,也就是说,人均纯收入在1 548.57元以上的农民家庭有1500户,在1547.57元以下的也有1500户。 中位数容易理解,不受极极端值影响,特别适宜于开口组数据资料和一些不能用数字测定的事物, 这是其优点,但是,我们有必须注意到它的灵敏度和计算功能较差,特别是当总体中的数据有间断数的 话,其作为代表值的功用就会削弱 3.其它分位数 所谓分位数就是把数据进行等分后位于等分点上的数据值,中位数就是一个二分位数。除了中位数 外,常用的分位数还有四分位数、八分位数和百分位数等。 (1)四分位数(Quartile) 四分位数又称为四分位点,它利用三个等分点将数据四等分:第一个等分点称为下四分位数,第二 个等分点就是中位数,第三个等分点称为上四分位数。 四分位数的计算方法与中位数相 先确定其位置,再确定其数值 a.顺序数据中四分位数位置的确定。 Q位置=(l,23》 (39) 式中,Q,是第i个四分位数,n是数据个数即总体单位数。 [例3-8]利用例3-4的数据确定四分位数。 g,位置=”=300=750 ,=不满意 42 Q位置=2-2×300-1500 Q,=一般 4
7 示中位数所在组的次数; M e d 表示中位数所在组的组距。 [例 3-7] 根据表 3-6 数据,计算农民家庭年人均纯收入中位数。 表 3-6 农民家庭年人均纯收入累计次数表 年人均纯收入(元) 农民家庭数(户) 向上累计户数 向下累计户数 1 000~1 200 240 240 3 000 1 200~1 400 480 720 2 760 1 400~1 600 1 050 1 770 2 280 1 600~1 800 600 2 370 1 230 1 800~2 000 270 2 640 630 2 000~2 200 210 2 850 360 2 200~2 400 120 2 970 150 2 400~2 600 30 3 000 30 合 计 3 000 — — 1 3000 2 1050 720 2 1400 200 1548.57 e e e e M e M M M f S M L d f - Â - = + ¥ = - + ¥ = ( 元 ) 1 3000 2 1050 1230 2 1600 200 1548.57 e e e e M e M M M f S M U d f + Â - = - ¥ = - - ¥ = ( 元 ) 计算表明,这 3 000 户农民家庭年人均纯收入的中位数是 1 548.57 元,也就是说,人均纯收入在 1 548.57 元以上的农民家庭有 1 500 户,在 1 547.57 元以下的也有 1 500 户。 中位数容易理解,不受极极端值影响,特别适宜于开口组数据资料和一些不能用数字测定的事物, 这是其优点,但是,我们有必须注意到它的灵敏度和计算功能较差,特别是当总体中的数据有间断数的 话,其作为代表值的功用就会削弱。 3.其它分位数 所谓分位数就是把数据进行等分后位于等分点上的数据值,中位数就是一个二分位数。除了中位数 外,常用的分位数还有四分位数、八分位数和百分位数等。 (1)四分位数(Quartile) 四分位数又称为四分位点,它利用三个等分点将数据四等分:第一个等分点称为下四分位数,第二 个等分点就是中位数,第三个等分点称为上四分位数。 四分位数的计算方法与中位数相似,先确定其位置,再确定其数值。 a.顺序数据中四分位数位置的确定。 4 i i n Q × 位置 = (i=1,2,3)。 (39) 式中,Qi 是第 i 个四分位数,n 是数据个数即总体单位数。 [例 3-8]利用例 3-4 的数据确定四分位数。 1 3000 750 4 2 n Q 位置 = = = Q1 = 不满意 2 2 2 3000 1500 4 4 n Q ¥ 位置 = = = Q2 = 一般

Q,位置-”-30-250Q=满意 b.未分组和单项式分组的数量数据中四分位数位置的确定: Q位置=+(1.2,3. (3-10) 第一个四分位数的位置:Q位置=”+ (3-11 A 第二个四分位数的位置:Q,位置=20-” (312) 第三个四分位数的位置:Q,位置=3仙+) (3-13) 4 [例3-9]计算例35中数据的四分位数。 0位置-”中-}-258=5+025-5-194020-19=1925 g位限”-号45g=兰223.2 Q位置=+=6750,=+075-)=23+0,7523-23)=23 4 从本例可以发现,当四分位数的位置不在某个数值上时,应当根据四分位数的位置,按照比例分 四分位数两边的数据 在单项式分组的数量数据中确定四分位数位置的方法与未分组数据的方法一样,只是要根据累计频 数或累计频率来确定。 c组距式分组数量数据中四分位数位置的确定: - g,=6+ (3-14) 式中,L®表示第i个分位数所在组的下限:Σ∫数据个数,即整体单位数:S。-表示向上累计至 第i个分位数所在组前一组的次数:。表示第i个分位数所在组的次数:d。表示第i个分位数所在组 的组距。 [例3-10]利用表3-6的数据确定四分位数。 EL-Sa 3000-720 g=%+ d=1400+ 1050 20=1405.71 1050×200=1548.57 3×3000-1770 =e+4 6%=1600+ 600 ×200=1760 (2)百分位数(Percentile) 百分位数是数据顺序排列后,将数据100等分,位于1(i=1,2,.,99)个等分点位置的数据值。 8
8 3 3 3 3000 2250 4 4 n Q ¥ 位置 = = = Q3 = 满意 b.未分组和单项式分组的数量数据中四分位数位置的确定: ( 1) 2 i i n Q + 位置 = (i=1,2,3)。 (310) 第一个四分位数的位置: 1 1 4 n Q + 位置 = (311) 第二个四分位数的位置: 2 2( 1) 1 4 2 n n Q + + 位置 = = (312) 第三个四分位数的位置: 3 3( 1) 4 n Q + 位置 = (313) [例 3-9] 计算例 35 中数据的四分位数。 1 1 9 2.25 4 4 n Q + 位置 = = = 1 2 3 2 Q = x + 0.25(x - x ) = 19 + 0.25(20 -19) = 19.25 2 1 9 4.5 2 2 n Q + 位置 = = = 4 5 2 22 23 22.5 2 2 x x Q + + = = = 3 3( 1) 6.75 4 n Q + 位置 = = 3 6 7 6 Q = x + 0.75(x - x ) = 23 + 0.75(23 - 23) = 23 从本例可以发现,当四分位数的位置不在某个数值上时,应当根据四分位数的位置,按照比例分摊 四分位数两边的数据差值。 在单项式分组的数量数据中确定四分位数位置的方法与未分组数据的方法一样,只是要根据累计频 数或累计频率来确定。 c.组距式分组数量数据中四分位数位置的确定: 1 4 i i i i Q i Q Q Q i f S Q L d f - × Â - = + × (314) 式中, Q i L 表示第 i 个分位数所在组的下限;Â f 数据个数,即整体单位数; 1 Q i S - 表示向上累计至 第 i 个分位数所在组前一组的次数; Q i f 表示第 i 个分位数所在组的次数; Q i d 表示第 i 个分位数所在组 的组距。 [例 3-10] 利用表 3-6 的数据确定四分位数。 1 1 1 1 1 1 3000 720 4 4 1400 200 1405.71 1050 Q Q Q Q f S Q L d f - Â - - = + × = + ¥ = 2 2 2 2 1 2 3000 720 4 2 1400 200 1548.57 1050 Q Q Q Q f S Q L d f - Â - - = + × = + ¥ = 3 3 3 3 1 3 3 3000 1770 4 4 1600 200 1760 600 Q Q Q Q f S Q L d f - Â ¥ - - = + × = + ¥ = (2)百分位数(Percentile) 百分位数是数据顺序排列后,将数据 100 等分,位于 i(i=1,2,.,99)个等分点位置的数据值

可见,第25百分位数就是第一个四分位数:第50百分位数即第二个四分位数,也就是中位数:第75 百分位数则是第三个四分位数。 百分位数的计算思路与四分位数一样。 需要说明的是,分位数是用于衡量数据的位置的测定指标,但它所衡量的不一定是中心位置。百分 位数提供了有关各数据项如何在最小值与最大值之间分布的信息。对于没有大量重复的数据,第1百分 位数将它分为两个部分。大约i%的数据项的值比第i百分位数小:而大约(100-i)%的数据项的值 比第i百分位数大。 对第i百分位数,严格的定义如下:第1百分位数是这样一个值,它使得至少有i%的数据项小于 或等于这个值,且至少有(100一1)%的数据项大于或等于这个值。 3.1.3数值平均数 数值平均数又称为均值,是用于测定数量数据的集中趋势的指标,算术平均数是最常用的数值平均 数,由算术平均数又引申出了调和平均数和几何平均数。 1.筐术平均数(均值)(arithmetic mean(mean) 算术平均数又称均值, 是统 十数据高低相互抵消后的结果,表现了数据的集中趋势和代表性水平 从统计思想看,均值削弱了数据中偶然性,揭示了蕴含在偶然性当中的必 然性,是统计数据集中趋势的一个最重要特征值。而且本身具有良好的数学性质。 (1)基本形式 算术平均数= 总体标志总量 (3-15) 体单位总新 算术平均数的计算条件:算术平均数是同质总体的标志总量和单位总数的比率关系 ,它要求基本公 式的分子(总体标志总量)与分母(总体单位总量)必须是同一总体,并且分子与分母在数量上存在若 直接的、 ·一的对应关系,即其分子(总体标志总量)数值要随者分母(总体单位总量)数值的变动而 变动。如100个职工所组成总体,其工资总额130000元,则平均工资就是130000/100-1300元:现在假 设其中的职工甲离开了该总体,甲的工资是1500元,则新总体的相关情况改变为:单位数99人,标志 总量128500,平均 资12 1297.98元 算术平均数的这一计算要求也是其与强度相对数的主要区别之一 算术平均数与强度相对数有相似之处:两者都是两个绝对数(总量指标)对比,并且有的强度相对 数还带有平均的含义:两者的都有计量单位,而且,计量单位也都是双重单位。但是两者有明显区别。 主要表现: 指标含义不同。强度相对数说明的是某一现象在另一现象中发展的强度、密度或普遍程度:而算 术平均数说明的是现象发展的一般水平。 b计算方法不同。强度相对数与算术平均数虽然都是两个有联系的总量指标之比,但是,强度相对 数分子与分母的联系,只表现为一种相互关系,其分子与分母在数量上不存在若直接的一一对应关系, 而算术平均数是在一个同质总体内标志总量与它自身的单位总量的比例关系,分子与分母的联系是一种 内在的联系,即其分子与分母在数量上存在者直接的 一对应关系 人均消费支出是消费总支出与人口数之比,消费支出与人口数有直接的 对应关系,故人均 消费支出是算术平均数:而人均国内生产总值是国内生产总值与人口数的比率,二者间不存在直接的 一对应关系。所以,人均国内生产总值是一个强度相对数。 实际工作中,由于数据的不同,算术平均数有简单算术平均数和加权算术平均数两种计算形式。 (2)简单算术平均数(simple arithmetic mean) 简单算术平均数主要用于未分组数据,用总体各单位标志值简单加总得到的标志总量除以单位总量 而得。计算公式如下:
9 可见,第 25 百分位数就是第一个四分位数;第 50 百分位数即第二个四分位数,也就是中位数;第 75 百分位数则是第三个四分位数。 百分位数的计算思路与四分位数一样。 需要说明的是,分位数是用于衡量数据的位置的测定指标,但它所衡量的不一定是中心位置。百分 位数提供了有关各数据项如何在最小值与最大值之间分布的信息。对于没有大量重复的数据,第 i 百分 位数将它分为两个部分。大约 i%的数据项的值比第 i 百分位数小;而大约(100-i)%的数据项的值 比第 i 百分位数大。 对第 i 百分位数,严格的定义如下:第 i 百分位数是这样一个值,它使得至少有 i%的数据项小于 或等于这个值,且至少有(100-i)%的数据项大于或等于这个值。 3.1.3 数值平均数 数值平均数又称为均值,是用于测定数量数据的集中趋势的指标,算术平均数是最常用的数值平均 数,由算术平均数又引申出了调和平均数和几何平均数。 1.算术平均数(均值) (arithmetic mean (mean) 算术平均数又称均值,是统计数据高低相互抵消后的结果,表现了数据的集中趋势和代表性水平。 从统计思想看,均值削弱了数据中偶然性,揭示了蕴含在偶然性当中的必 然性,是统计数据集中趋势的一个最重要特征值。而且本身具有良好的数学性质。 (1)基本形式 = 总体标志总量 算术平均数 总体单位总数 (315) 算术平均数的计算条件:算术平均数是同质总体的标志总量和单位总数的比率关系,它要求基本公 式的分子(总体标志总量)与分母(总体单位总量)必须是同一总体,并且分子与分母在数量上存在着 直接的、一一的对应关系,即其分子(总体标志总量)数值要随着分母(总体单位总量)数值的变动而 变动。如 100 个职工所组成总体,其工资总额 130000 元,则平均工资就是 130000/100=1300 元;现在假 设其中的职工甲离开了该总体,甲的工资是 1500 元,则新总体的相关情况改变为:单位数 99 人,标志 总量 128500,平均工资 128500/99=1297.98 元。 算术平均数的这一计算要求也是其与强度相对数的主要区别之一。 算术平均数与强度相对数有相似之处:两者都是两个绝对数(总量指标)对比,并且有的强度相对 数还带有平均的含义;两者的都有计量单位,而且,计量单位也都是双重单位。但是两者有明显区别。 主要表现: a.指标含义不同。强度相对数说明的是某一现象在另一现象中发展的强度、密度或普遍程度;而算 术平均数说明的是现象发展的一般水平。 b.计算方法不同。强度相对数与算术平均数虽然都是两个有联系的总量指标之比,但是,强度相对 数分子与分母的联系,只表现为一种相互关系,其分子与分母在数量上不存在着直接的一一对应关系, 而算术平均数是在一个同质总体内标志总量与它自身的单位总量的比例关系,分子与分母的联系是一种 内在的联系,即其分子与分母在数量上存在着直接的一一对应关系。 如,人均消费支出是消费总支出与人口数之比,消费支出与人口数有直接的一一对应关系,故人均 消费支出是算术平均数;而人均国内生产总值是国内生产总值与人口数的比率,二者间不存在直接的一 一对应关系。所以,人均国内生产总值是一个强度相对数。 实际工作中,由于数据的不同,算术平均数有简单算术平均数和加权算术平均数两种计算形式。 (2)简单算术平均数(simple arithmetic mean) 简单算术平均数主要用于未分组数据,用总体各单位标志值简单加总得到的标志总量除以单位总量 而得。计算公式如下:

不=++.+五=白 (316) 式中,下代表算术平均数,x,表各单位标志值,n代表总体单位数。 [例3-11]例3-5的中,日产零件数分别为17、19、20、22、23、23、24、25(件/人)8名工人 的日产零件的平均数为: ._7+19+20+2+23+23+24+25-21625件1人 8 (3)加权算术平均数(weighted arithmetic mean) 加权算术平均数主要用于数据已经分组,并编制出次数分布的条件下。这时必须先将各组标志值乘 以相应的次数,得到各组的标志总量,然后再相加得到总体标志总量。加权算术平均数的计算公式为: (3-17) [例3-12】利用表3-2的数据计算算术平均数。 表3-7 教师平均开课门数计算表 开课门数 教师数 标志值 £(%) xf 三 1 15 15 17.65 0.1765 30 0 35.29 0.7058 3 28 84 32.94 0.9882 48 14.12 0.5648 合计 85 207 100.00 2.4353 0-245n 285 或按照频率计算:=5=2435X门) 说明该院教师该学年平均开课门数为2.45门。 如果是组距式分组,在假定各组内的变量值均匀分布的条件下,用各组的组中值代表各组的平均值 以各组组中值乘以各组次数作为各组的标志总最,再计算总平均数。 筒3利用表3与数据计第草术平均发
10 n x n x x x x n i i n Â= = + + + = 1 2 L 1 (316) 式中, x 代表算术平均数,xi 表各单位标志值,n 代表总体单位数。 [例 3-11] 例 3-5 的中,日产零件数分别为 17、19、20、22、23、23、24、25(件/人)8 名工人 的日产零件的平均数为: 1 17 19 20 22 23 23 24 25 21.625( / 8 n i i x x n = Â + + + + + + + = = = 件 人) (3)加权算术平均数(weighted arithmetic mean) 加权算术平均数主要用于数据已经分组,并编制出次数分布的条件下。这时必须先将各组标志值乘 以相应的次数,得到各组的标志总量,然后再相加得到总体标志总量。加权算术平均数的计算公式为: 1 1 2 2 1 1 1 2 1 1 n i i n n n i i n i n i n i i i i x f x f x f x f f x x f f f f f = = + = = Â × + + + = = = Â + + Â Â L L (317) [例 3-12] 利用表 3-2 的数据计算算术平均数。 表 3-7 教师平均开课门数计算表 开课门数 i x 教师数 i f 标志值 i i x × f 1 i n i i f f = Â (%) 1 i i n i i f x f = × Â 1 15 15 17.65 0.1765 2 30 60 35.29 0.7058 3 28 84 32.94 0.9882 4 12 48 14.12 0.5648 合计 85 207 100.00 2.4353 1 1 207 2.4353 85 n i i i n i i x f x f = = Â × = = = Â (门) 或按照频率计算: 1 1 2.4353 n i i n i i i f x x f = = = Â = Â (门) 说明该院教师该学年平均开课门数为 2.45 门。 如果是组距式分组, 在假定各组内的变量值均匀分布的条件下, 用各组的组中值代表各组的平均值, 以各组组中值乘以各组次数作为各组的标志总量,再计算总平均数。 [例 313] 利用表 33 数据计算算术平均数