
二、卡诺定理 二、卡诺定理 在T和T,两热源之间工作的所有热机中可逆热机(卡诺热机)效率最 大。 n卡>n (证明略) 三、卡诺定理推论 在T和T2两热源之间工作的所有可逆热机效率相等,与工作物质 的性质无关。 η卡=n'(证明略) 结论: T-五≥g+9 9 ≤0 不 T T 可
二、卡诺定理 在T1和T2两热源之间工作的所有热机中可逆热机(卡诺热机)效率最 大。 卡 (证明略) 三、卡诺定理推论 在T1和T2两热源之间工作的所有可逆热机效率相等,与工作物质 的性质无关。 卡 = (证明略) 1 1 2 1 1 2 Q Q Q T T T + − 结论: 0 2 2 1 1 + T Q T Q 不 可 二、卡诺定理

§3-4熵、亥母霍兹函数、吉布斯函数 Entropy,Helmholz function,Gibbs function -Derive entropy and define entropy The property of entropy and calculate the change of entropy 三、Equation of the second law 四、Helmholz function and its criteria 。 五、Gibbs function and its criteria ·六、The meaning of△A、△G
§3-4 熵、亥母霍兹函数、吉布斯函数 Entropy,Helmholz function,Gibbs function • 一、Derive entropy and define entropy • 二、The property of entropy and calculate the change of entropy • 三、Equation of the second law • 四、Helmholz function and its criteria • 五、Gibbs function and its criteria • 六、The meaning of A、G

、 熵的定义与导出 Derive entropy and define entropy 对任意可逆循环ABCDA(光 可 滑曲线)作许多绝热可逆 (红色)线分割,再作等温可 逆(棕色)线与相邻的两绝热 可逆线相交,使许多小卡诺 循环组成的面积与原ABCDA所 围面积相等。(见左上图) V/[V]
对任意可逆循环ABCDA(光 滑曲线)作许多绝热可逆 (红色)线分割,再作等温可 逆(棕色)线与相邻的两绝热 可逆线相交,使许多小卡诺 循环组成的面积与原ABCDA所 围面积相等。(见左上图) 一、熵的定义与导出 Derive entropy and define entropy P p
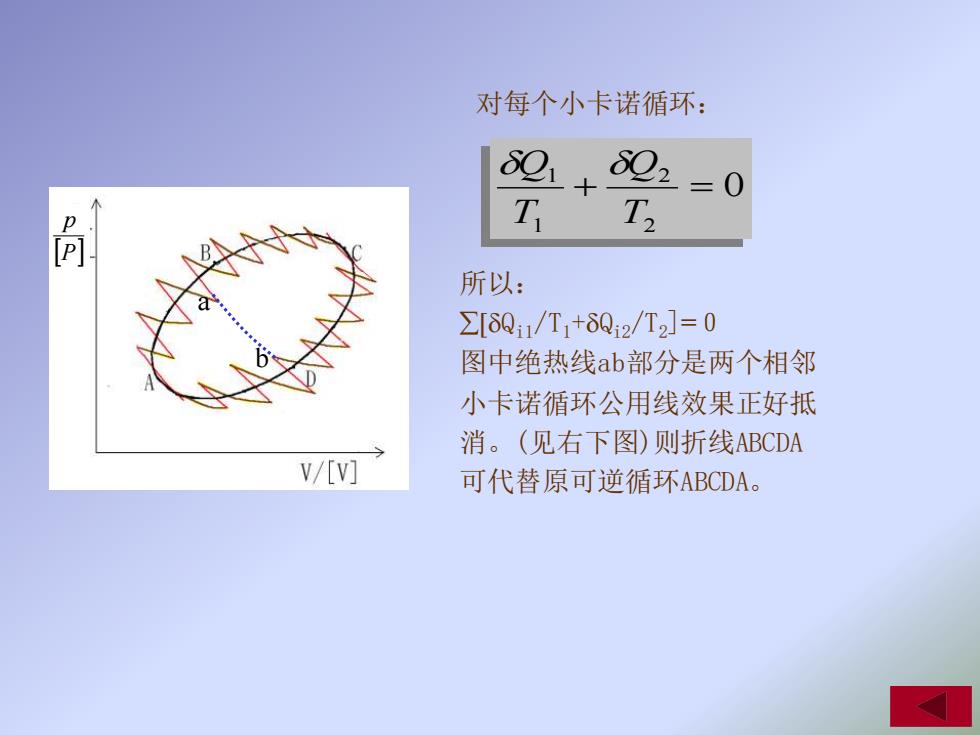
对每个小卡诺循环: 821 802 0 T T 所以: ∑[δQ11/T1+δQ12/T2]=0 图中绝热线ab部分是两个相邻 小卡诺循环公用线效果正好抵 消。(见右下图)则折线ABCDA V/[V] 可代替原可逆循环ABCDA
所以: [Qi1/T1+Qi2/T2]=0 图中绝热线ab部分是两个相邻 小卡诺循环公用线效果正好抵 消。(见右下图)则折线ABCDA 可代替原可逆循环ABCDA。 对每个小卡诺循环: 0 2 2 1 1 + = T Q T Q a b P p
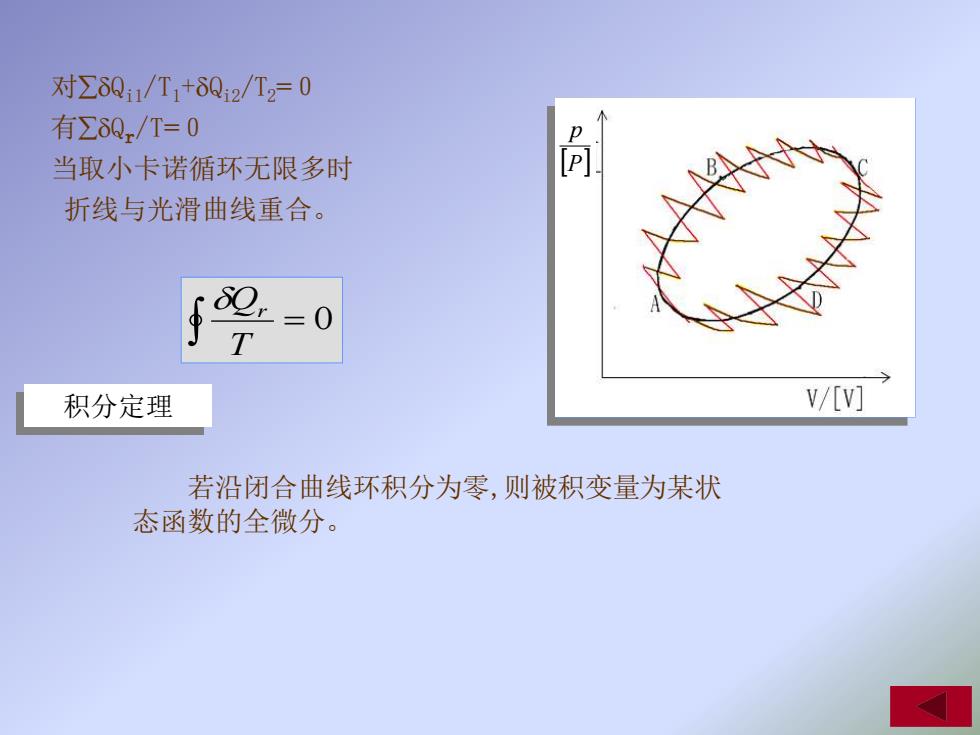
对∑6Q1/T1+6Q2/T20 有∑ò0/T=0 当取小卡诺循环无限多时 折线与光滑曲线重合。 T =0 积分定理 V/[V叮 若沿闭合曲线环积分为零,则被积变量为某状 态函数的全微分
P p 对Qi1/T1+Qi2/T2=0 有Qr/T=0 当取小卡诺循环无限多时 折线与光滑曲线重合。 = 0 T Qr 积分定理 若沿闭合曲线环积分为零,则被积变量为某状 态函数的全微分