
思考: ①配位数为4的正四面体结构的配位 化合物是否有顺、反异构体? ②配位数为6的八面体结构的配位化 无机化学电子救 合物是否有顺、反异构体?
思考: ① 配位数为4的正四面体结构的配位 化合物是否有顺、反异构体? ② 配位数为6的八面体结构的配位化 合物是否有顺、反异构体?
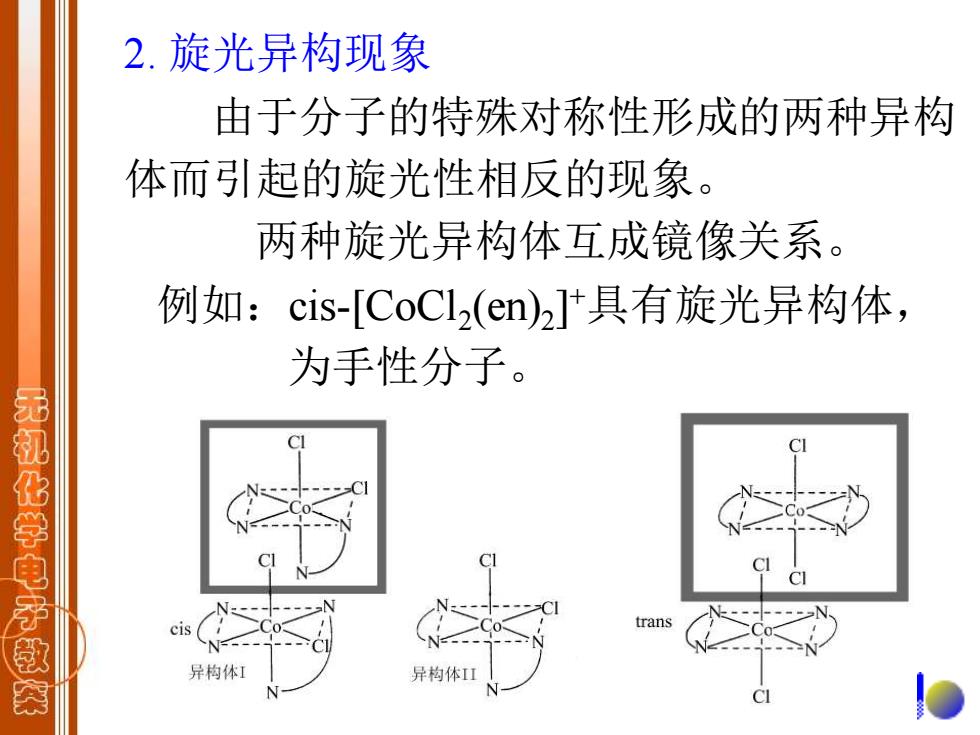
2.旋光异构现象 由于分子的特殊对称性形成的两种异构 体而引起的旋光性相反的现象。 两种旋光异构体互成镜像关系。 例如:cis-[CoCl2(en)2]具有旋光异构体, 为手性分子。 无机化学电子救 cis trans 异构体I 异构体山
2. 旋光异构现象 由于分子的特殊对称性形成的两种异构 体而引起的旋光性相反的现象。 两种旋光异构体互成镜像关系。 例如:cis-[CoCl2 (en)2 ] +具有旋光异构体, 为手性分子

11.1.3配合物的磁性 磁 性:物质在磁场中表现出来的性质。 磁矩:u=√nn+2)(B.M)玻尔磁子 n一未成对电子数 顺磁性: 被磁场吸引4>0,n>0。 无机化学电子 例:O2,NO,NO2 反磁性:被磁场排斥u=0,n=0。例:H2,N2 铁磁性:被磁场强烈吸引。例:Fe,Co,Ni
11.1.3 配合物的磁性 n — 未成对电子数 顺磁性:被磁场吸引 µ > 0 , n > 0 。 例:O2,NO,NO2 反磁性:被磁场排斥 µ = 0 , n =0。例:H2 ,N2 铁磁性:被磁场强烈吸引。例:Fe,Co,Ni 磁 性:物质在磁场中表现出来的性质。 磁 矩: = n(n+ 2) (B.M.)玻尔磁子

根据u=Vn(n+2)可用未成对电子 数目n估算磁矩u。 n 0 2 3 4 5 u/B.M. 01.732.833.87 4.905.92 羞 实例: 化学电 [Ti(H2O)6]3+ Ti3+: 3d1 u=1.73 n=1 K3[Mn(CN)] Mn3+: 3d4 u=3.18 n=2 数 K3[Fe(CN)] Fe3+: 3d5 w=2.40 n=1
n 0 1 2 3 4 5 µ/B.M. 0 1.73 2.83 3.87 4.90 5.92 实例: [Ti(H2O)6 ] 3+ Ti3+: 3d1 µ =1.73 n=1 K3 [Mn(CN)6 ] Mn3+: 3d4 µ =3.18 n=2 K3 [Fe(CN)6 ] Fe3+: 3d5 µ =2.40 n=1 根据 = n(n+ 2) 可用未成对电子 数目n估算磁矩µ

§11.2配合物的化学候理论 11.2.1 价键理论 11.2.2 晶体场理论 *11.2.3 分子轨道理论 回
§11.2 配合物的化学键理论 11.2.1 价键理论 11.2.2 晶体场理论 *11.2.3 分子轨道理论