
3.2力对点的矩和力对轴的矩 思考:空间问题中力对点的矩用矢量表示还是用代数量 表示? ·一力对点的矩以矢量表示-一一一力矩矢 Mo(F) B M(F) 作用在0点 大小 定位矢量 方向 Mo(F)=r×F 18
18 3.2 力对点的矩和力对轴的矩 ❖ 一 力对点的矩以矢量表示-力矩矢 M F O ( ) O r MO(F) 思考:空间问题中力对点的矩用矢量表示还是用代数量 表示? M F r F O ( ) = 作用在O点 定位矢量 F B 大小 A 方向 h
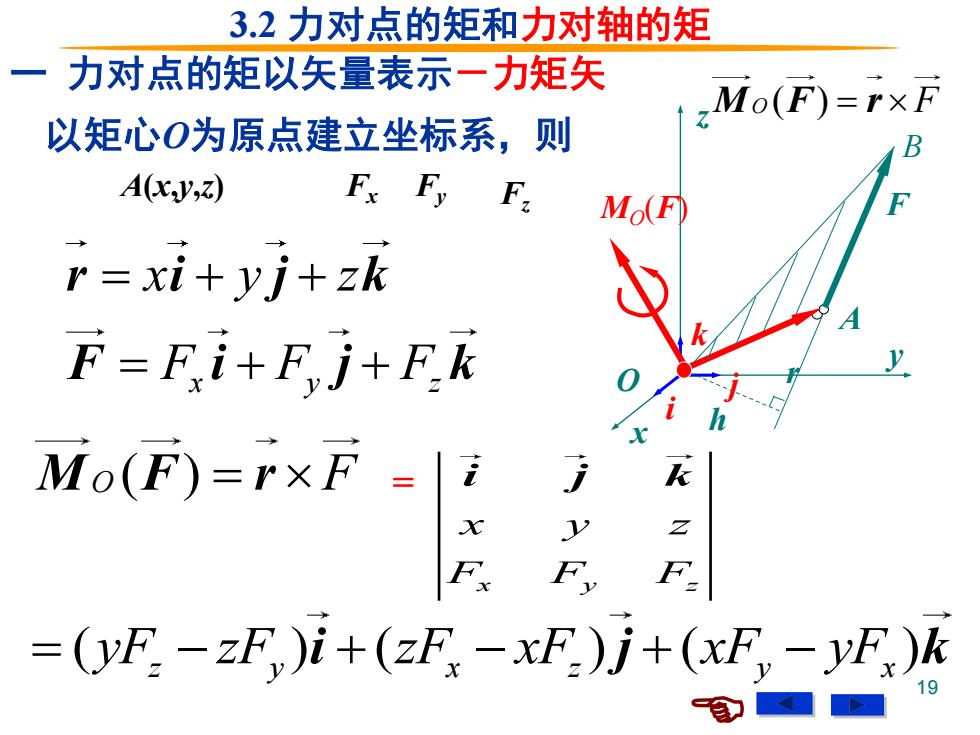
3.2力对点的矩和力对轴的矩 力对点的矩以矢量表示一力矩矢 zMo(F)=rxF 以矩心O为原点建立坐标系,则 B A(xy,) Fx Fy F. M(F) r=xi+yj+zk F=Fi+Fj+Fk Mo(F)=rxF=i =(yF,-zF)i+(zF,-xF.)j+(xF,-yF)k 9
19 以矩心O为原点建立坐标系,则 x y z x y z F F F = + + = + + r i j k F i j k M F r O ( ) = F A(x,y,z) x y z j i k 一 力对点的矩以矢量表示-力矩矢 x y z x y z F F F i j k ( ) ( ) ( ) z y x z y x = − + − + − yF zF zF xF xF yF i j k = F B A O r MO(F) h Fx Fy Fz M F r O ( ) = F 3.2 力对点的矩和力对轴的矩
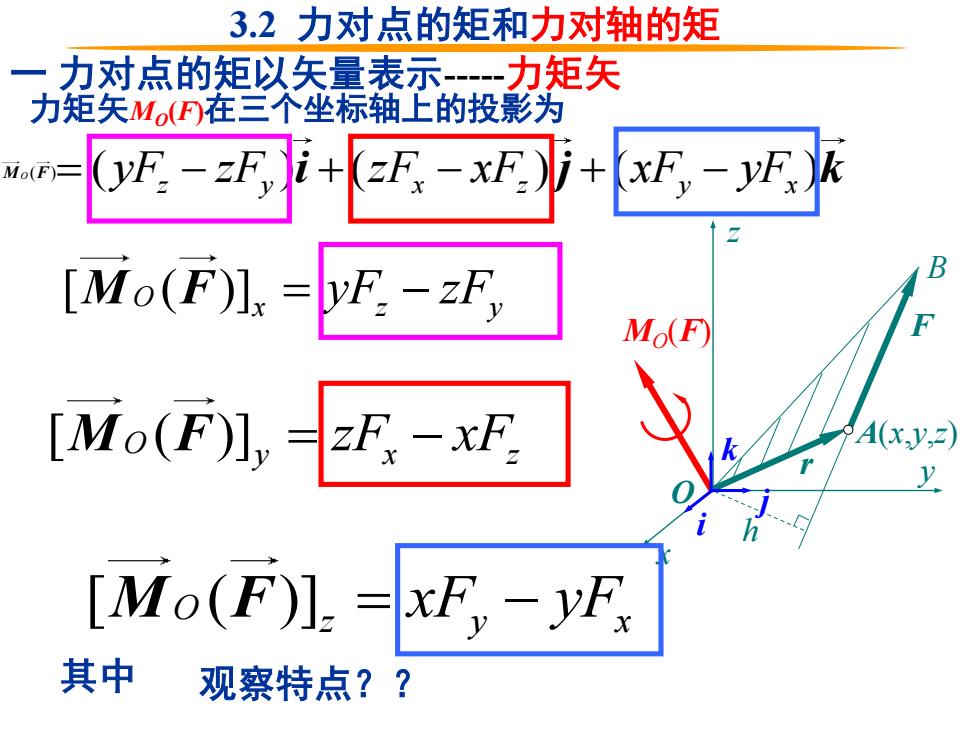
3.2力对点的矩和力对轴的矩 一力对点的矩以矢量表示-力矩矢 力矩矢Mo(F在三个坐标轴上的投影为 Mo(F)- -5 =F,-xF.)j+xF,-yF,) [Mo(F)],=yF:-zF, Mo(F) [Mo(F)],=zF,-xF. A(x.y,) [Mo(F】=xF-yF 其中 观察特点??
力矩矢MO(F)在三个坐标轴上的投影为 [ ( )] O x z y M F = − yF zF x y z O M F O(F) r A(x,y,z) h B j i k 一 力对点的矩以矢量表示-力矩矢 [ ( )] O y x z M F = − zF xF [ ( )] O z y x M F = − xF yF ( ) ( ) ( ) z y x z y x = − + − + − yF zF zF xF xF yF i j k 其中 观察特点?? 3.2 力对点的矩和力对轴的矩 M F O ( )
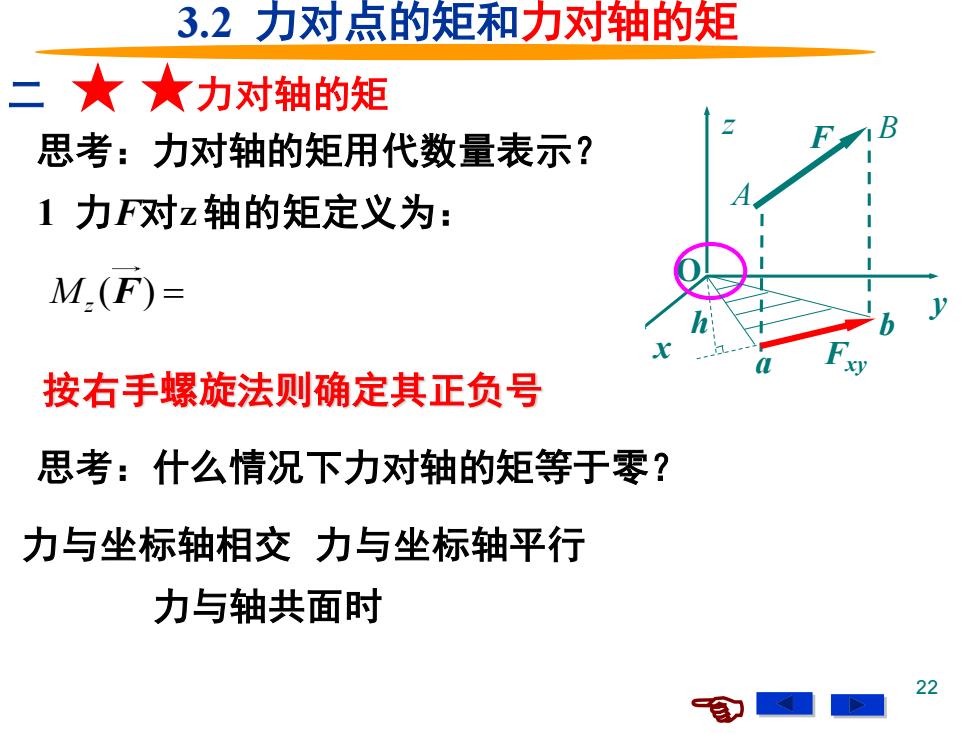
3.2力对点的矩和力对轴的矩 二★★力对轴的矩 思考:力对轴的矩用代数量表示? 1力对z轴的矩定义为: M.(F)= 按右手螺旋法则确定其正负号 思考:什么情况下力对轴的矩等于零? 力与坐标轴相交力与坐标轴平行 力与轴共面时 22
22 1 力F对z 轴的矩定义为: ( ) ( ) 2 M M F h A z O xy xy Oab F F = = = 二 ★ ★力对轴的矩 z F B A 按右手螺旋法则确定其正负号 思考:力对轴的矩用代数量表示? 思考:什么情况下力对轴的矩等于零? 力与轴共面时 y x O a Fxy h b 3.2 力对点的矩和力对轴的矩 力与坐标轴相交 力与坐标轴平行
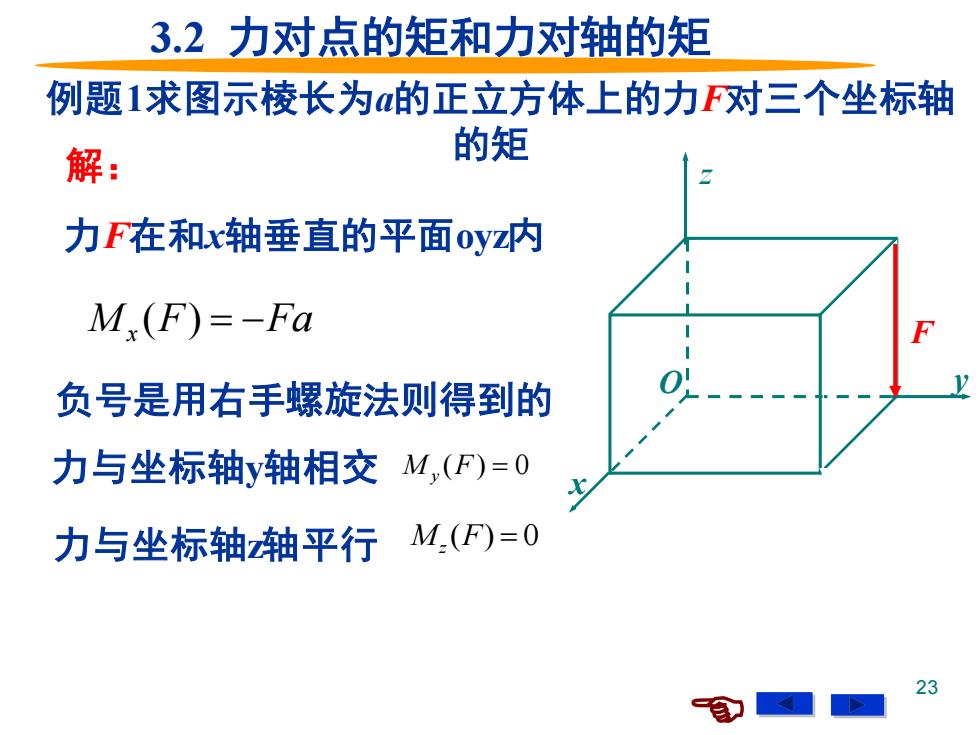
3.2力对点的矩和力对轴的矩 例题1求图示棱长为的正立方体上的力F对三个坐标轴 解: 的矩 力F在和x轴垂直的平面oyz内 M,(F)=-Fa 负号是用右手螺旋法则得到的 力与坐标轴y轴相交M,(F)=0 力与坐标轴轴平行 M(F)=0 23
23 例题1求图示棱长为a的正立方体上的力F对三个坐标轴 的矩 z x O y F 3.2 力对点的矩和力对轴的矩 负号是用右手螺旋法则得到的 Mx (F) = −Fa 力与坐标轴z轴平行 M y (F) = 0 M z (F) = 0 解: 力F在和x轴垂直的平面oyz内 力与坐标轴y轴相交