
存款总额的乘积。法定存款准备金率是各国货币管理当局规定的存款缴存比例, 它是中央银行控制货币供应量的最重要手段之一。法定准备率越高,则银行吸收 的存款用于贷款的数额越少,货币供应量减少:反之,则越多。超额准备金是商 业银行准备金中超过法定的部分。 由于部分准备金制度的存在,银行在吸收进一笔现金或支票后,留存一部分 准备,就可以将其余部分用于贷款,存款派生机制也才会存在。假若银行实行的 是全额准备金制度,则商业银行除了将存款放入保险柜或存入中央银行外,再无 其他活动,这样,存款也就不可能派生。银行在全额准备金制度下不能得到任何 利益,储户也就不可能得到任何的存款利息。因此,部分存款准备金制度不但是 存款派生的前提条件,更是银行体系存在的前提。对于一定数量的存款来说,准 备金的比例越高,银行可用于贷款的资金就越少,存款派生的能力就越低:反之, 准备金的比例越低,银行的存款派生能力就越强。如果银行实行零准备金制度, 则商业银行可以将存款以贷款的形式全额放出,在没有现金漏出的条件下,这些 贷款会重新回到商业银行成为存款,如此不断循环,从而在理论上可以无限制的 扩大货币供应量。 (二)非现金结算制度 非现金结算制度能使人们通过支票的形式进行货币支付,银行之间的往来进 行转账结算,无须使用现金。如果社会经济活动的所有交易都必须使用现金,那 么借款人在得到任何一笔贷款后都会立刻以现金的形式取出,直到贷款归还以前 这笔资金都在银行体系之外流通,而不被存入银行,在这种情况下银行也无法创 造存款。在现实中,我们经常用现金漏出率来计算流通于银行体系之外的货币 数量。 因此,对于商业银行的存款创造过程而言,部分准备金制度和非现金结算制 度两者缺一不可。 二、多倍存款扩张的过程 ①现金漏出率的概念见本节的第三部分内容
存款总额的乘积。法定存款准备金率是各国货币管理当局规定的存款缴存比例, 它是中央银行控制货币供应量的最重要手段之一。法定准备率越高,则银行吸收 的存款用于贷款的数额越少,货币供应量减少;反之,则越多。超额准备金是商 业银行准备金中超过法定的部分。 由于部分准备金制度的存在,银行在吸收进一笔现金或支票后,留存一部分 准备,就可以将其余部分用于贷款,存款派生机制也才会存在。假若银行实行的 是全额准备金制度,则商业银行除了将存款放入保险柜或存入中央银行外,再无 其他活动,这样,存款也就不可能派生。银行在全额准备金制度下不能得到任何 利益,储户也就不可能得到任何的存款利息。因此,部分存款准备金制度不但是 存款派生的前提条件,更是银行体系存在的前提。对于一定数量的存款来说,准 备金的比例越高,银行可用于贷款的资金就越少,存款派生的能力就越低;反之, 准备金的比例越低,银行的存款派生能力就越强。如果银行实行零准备金制度, 则商业银行可以将存款以贷款的形式全额放出,在没有现金漏出的条件下,这些 贷款会重新回到商业银行成为存款,如此不断循环,从而在理论上可以无限制的 扩大货币供应量。 (二)非现金结算制度 非现金结算制度能使人们通过支票的形式进行货币支付,银行之间的往来进 行转账结算,无须使用现金。如果社会经济活动的所有交易都必须使用现金,那 么借款人在得到任何一笔贷款后都会立刻以现金的形式取出,直到贷款归还以前 这笔资金都在银行体系之外流通,而不被存入银行,在这种情况下银行也无法创 造存款。在现实中,我们经常用现金漏出率①来计算流通于银行体系之外的货币 数量。 因此,对于商业银行的存款创造过程而言,部分准备金制度和非现金结算制 度两者缺一不可。 二、多倍存款扩张的过程 ① 现金漏出率的概念见本节的第三部分内容

为了便于说明,我们假定:(1)客户将从银行得到的贷款全部存人银行,而 不提现金;(2)法定存款准备金比率为10%。假定A银行接受了客户存入的现金 10000元。按规定从中提取现金准备1000元,以应付客户提现的需要。其余9000 元可以用于贷款以取得收益。 A银行资产负债表 单位:元 资 产 负 债 现金准备 +1000 现金存款 +10000 贷款与投资 +9000 总额 +10000 总额 +10000 由于一国的商业银行有许多,当A银行将9000元贷给客户时,该客户可以 将钱存入B银行。B银行再按10%提取900元作现金准备,其余再贷放出去。 B银行资产负债表 单位:元 资 产 负 债 现金准备 +900 现金存款 +9000 贷款与投资 +8100 总额 +9000 总额 +9000 B银行贷出8100元,借款人又转存入C银行。C银行按10%提取准备金后, 其余再贷放出去。 C银行资产负债表 单位:元 资 产 负 债 现金准备 +810 现金存款 +8100 贷款与投资 +7290 总额 +8100 总额 +8100 如此类推,银行与客户之间不断地贷款、存款, 就会产生以下结果。 存款货币的创造过程 单位:元 银行 存款 现金准备 贷款
为了便于说明,我们假定:(1)客户将从银行得到的贷款全部存人银行,而 不提现金;(2)法定存款准备金比率为 10%。假定 A 银行接受了客户存入的现金 10000 元。按规定从中提取现金准备 1000 元,以应付客户提现的需要。其余 9000 元可以用于贷款以取得收益。 A 银行资产负债表 单位:元 资 产 负 债 现金准备 +1000 贷款与投资 +9000 总额 +10000 现金存款 +10000 总额 +10000 由于一国的商业银行有许多,当 A 银行将 9000 元贷给客户时,该客户可以 将钱存入 B 银行。B 银行再按 10%提取 900 元作现金准备,其余再贷放出去。 B 银行资产负债表 单位:元 资 产 负 债 现金准备 +900 贷款与投资 +8100 总额 +9000 现金存款 +9000 总额 +9000 B 银行贷出 8100 元,借款人又转存入 C 银行。C 银行按 10%提取准备金后, 其余再贷放出去。 C 银行资产负债表 单位:元 资 产 负 债 现金准备 +810 贷款与投资 +7290 总额 +8100 现金存款 +8100 总额 +8100 如此类推,银行与客户之间不断地贷款、存款,就会产生以下结果。 存款货币的创造过程 单位:元 银行 存款 现金准备 贷款
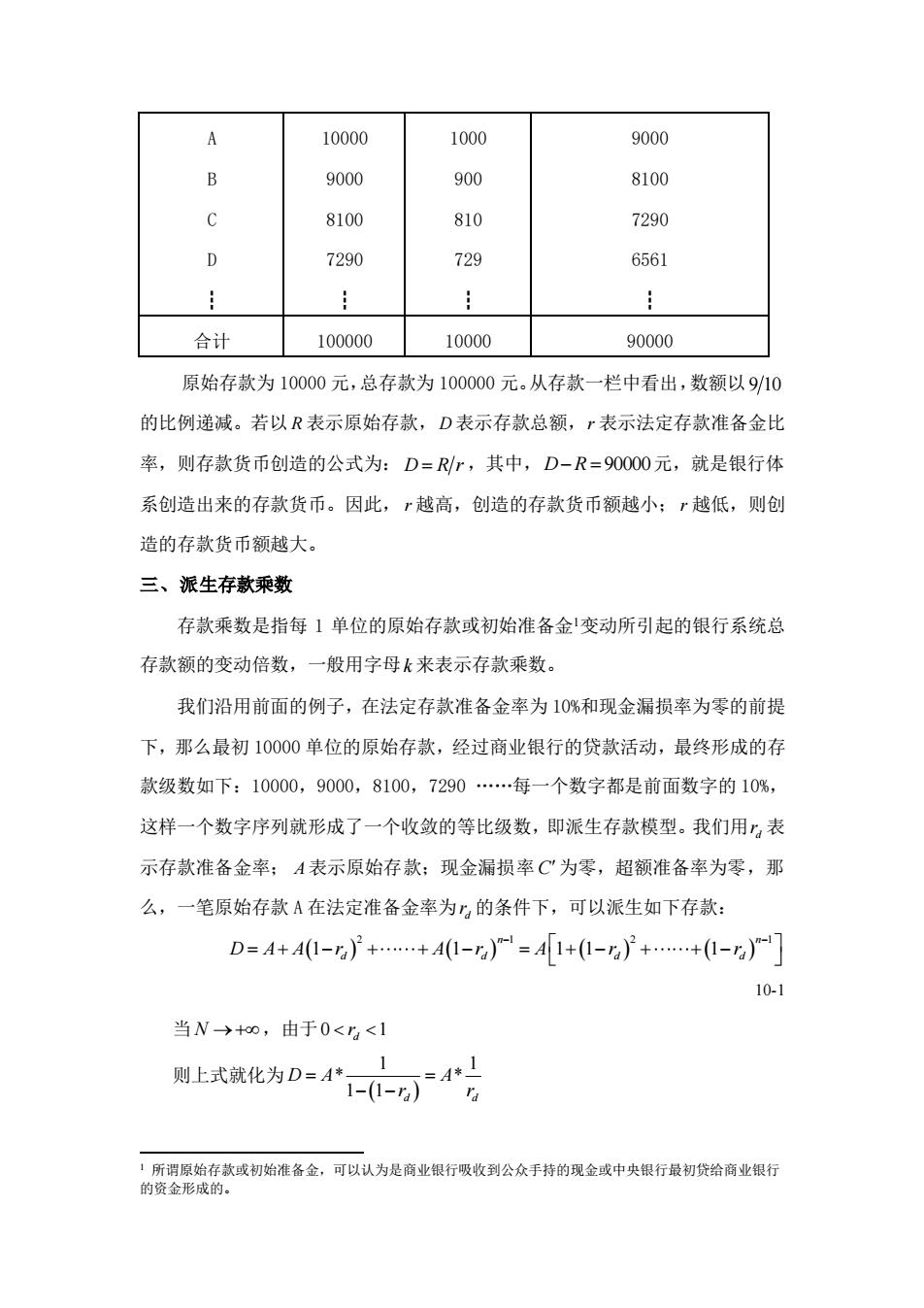
A 10000 1000 9000 B 9000 900 8100 8100 810 7290 D 7290 729 6561 合计 100000 10000 90000 原始存款为10000元,总存款为100000元。从存款一栏中看出,数额以9/10 的比例递减。若以R表示原始存款,D表示存款总额,r表示法定存款准备金比 率,则存款货币创造的公式为:D=R/r,其中,D-R=90000元,就是银行体 系创造出来的存款货币。因此,r越高,创造的存款货币额越小;r越低,则创 造的存款货币额越大。 三、派生存款乘数 存款乘数是指每1单位的原始存款或初始准备金变动所引起的银行系统总 存款额的变动倍数,一般用字母k来表示存款乘数。 我们沿用前面的例子,在法定存款准备金率为10%和现金漏损率为零的前提 下,那么最初10000单位的原始存款,经过商业银行的贷款活动,最终形成的存 款级数如下:10000,9000,8100,7290…每一个数字都是前面数字的10%, 这样一个数字序列就形成了一个收敛的等比级数,即派生存款模型。我们用”表 示存款准备金率;A表示原始存款;现金漏损率C'为零,超额准备率为零,那 么,一笔原始存款A在法定准备金率为的条件下,可以派生如下存款: D=A+A1-)++A(1-g)=A1+-g++1-)- 10-1 当N→+0,由于0<r<1 则上式就化为D=A*1 A* 1-(1-)h 1所谓原始存款或初始准备金,可以认为是商业银行吸收到公众手持的现金或中央银行最初贷给商业银行 的资金形成的
A B C D ┇ 10000 9000 8100 7290 ┇ 1000 900 810 729 ┇ 9000 8100 7290 6561 ┇ 合计 100000 10000 90000 原始存款为 10000 元,总存款为 100000 元。从存款一栏中看出,数额以 9 10 的比例递减。若以 R 表示原始存款, D 表示存款总额, r 表示法定存款准备金比 率,则存款货币创造的公式为: D R r = ,其中, D R− = 90000 元,就是银行体 系创造出来的存款货币。因此, r 越高,创造的存款货币额越小; r 越低,则创 造的存款货币额越大。 三、派生存款乘数 存款乘数是指每 1 单位的原始存款或初始准备金变动所引起的银行系统总 存款额的变动倍数,一般用字母 k 来表示存款乘数。 我们沿用前面的例子,在法定存款准备金率为 10%和现金漏损率为零的前提 下,那么最初 10000 单位的原始存款,经过商业银行的贷款活动,最终形成的存 款级数如下:10000,9000,8100,7290 ……每一个数字都是前面数字的 10%, 这样一个数字序列就形成了一个收敛的等比级数,即派生存款模型。我们用 d r 表 示存款准备金率; A 表示原始存款;现金漏损率 C 为零,超额准备率为零,那 么,一笔原始存款 A 在法定准备金率为 d r 的条件下,可以派生如下存款: ( ) ( ) ( ) ( ) 2 1 2 1 1 1 1 1 1 n n D A A r A r A r r d d d d − − = + − + + − = + − + + − 10-1 当 N → + ,由于 0 1 d r 则上式就化为 ( ) 1 1 * * 1 1 d d D A A r r = = − − 所谓原始存款或初始准备金,可以认为是商业银行吸收到公众手持的现金或中央银行最初贷给商业银行 的资金形成的

那么,1就是派生存款乘数,即K= 10-2 ra ra 四、派生存款乘数的修正 首先,在前面的分析中假定在存款创造过程中没有现金C从银行系统中漏 出。但在现实中由于种种原因,必然会存在一部分存款以现金的形式被公众提取 出来,并持续的保留在公众手中。虽然支票存款的流动性接近于现金,但在一些 小额交易或秘密交易中,人们还是不会采用支票的形式。这一现象在信用体制不 发达的国家更为普遍,毕竟只有现金才是最具流动性的支付手段。由于这部分现 金从银行体系漏出,也就不可能参与存款的创造,其作用与法定存款准备金率的 作用一致。如果用c表示平均每一元活期存款中公众持有的现金比例,可以根据 上述的收敛的等比级数公式10-1推算出在考虑现金漏损率情况下的新的模型, 即存款派生乘数的表达式可以写作: K=、1 10-3 ra+c 其次,前面假定所有银行都不持有超额准备金G,但为了保持流动性、避免 向中央银行借款,各个商业银行通常都持有一定的超额准备金,虽然这一比例比 较小。超额准备金的数额根据实际经济情况由银行自由掌握,但银行一旦持有了 超额准备金,那它对存款创造所起的作用和法定存款准备金完全相同。如果用g 表示平均每一元存款中银行持有的超额准备金的百分比,那么存款可以根据上述 的收敛的等比级数公式10-1推算出在考虑现金漏损率和超额准备金率条件下的 新的模型,即存款派生乘数的表达式可以扩展为: 1 K=- 10-4 +c+g 最后,我们还必须考虑到新增的活期(支票)存款向其他存款的转化。随着 活期存款的增加,其中一些将转变为非个人定期存款。由于法律规定银行对非个 人定期存款也需要持有一定比例的准备金,并且这一比率同活期存款的法定准备 金比率不同,因而这种转化会对存款派生比例产生影响。假定非个人定期存款的
那么, 1 d r 就是派生存款乘数,即 1 d K r = 10-2 四、派生存款乘数的修正 首先,在前面的分析中假定在存款创造过程中没有现金 C 从银行系统中漏 出。但在现实中由于种种原因,必然会存在一部分存款以现金的形式被公众提取 出来,并持续的保留在公众手中。虽然支票存款的流动性接近于现金,但在一些 小额交易或秘密交易中,人们还是不会采用支票的形式。这一现象在信用体制不 发达的国家更为普遍,毕竟只有现金才是最具流动性的支付手段。由于这部分现 金从银行体系漏出,也就不可能参与存款的创造,其作用与法定存款准备金率的 作用一致。如果用 c 表示平均每一元活期存款中公众持有的现金比例,可以根据 上述的收敛的等比级数公式 10-1 推算出在考虑现金漏损率情况下的新的模型, 即存款派生乘数的表达式可以写作: 1 ' d K r c = + 10-3 其次,前面假定所有银行都不持有超额准备金 G ,但为了保持流动性、避免 向中央银行借款,各个商业银行通常都持有一定的超额准备金,虽然这一比例比 较小。超额准备金的数额根据实际经济情况由银行自由掌握,但银行一旦持有了 超额准备金,那它对存款创造所起的作用和法定存款准备金完全相同。如果用 g 表示平均每一元存款中银行持有的超额准备金的百分比,那么存款可以根据上述 的收敛的等比级数公式 10-1 推算出在考虑现金漏损率和超额准备金率条件下的 新的模型,即存款派生乘数的表达式可以扩展为: 1 ' g d K r c = + + 10-4 最后,我们还必须考虑到新增的活期(支票)存款向其他存款的转化。随着 活期存款的增加,其中一些将转变为非个人定期存款。由于法律规定银行对非个 人定期存款也需要持有一定比例的准备金,并且这一比率同活期存款的法定准备 金比率不同,因而这种转化会对存款派生比例产生影响。假定非个人定期存款的

比例为1,非个人定期存款的准备金比率为r,那么每一元活期存款中就会有r 作为法定准备金从存款派生体系中漏出,那么根据上述10-1式原理,从而派生 存款乘数进一步扩展为: 1 K=- 10-5 +c+8+tr 第三节货币供应的理论模型 一、货币供给与银行体系的合并资产负债表 货币供给与银行体系的资产负债业务有着密切的关系,因为,流通中的现金 是中央银行对大众的负债:银行存款又是商业银行对存款部门的负债。通过分析 银行机构的资产负债的关系而揭示货币供给的决定因素。 (一)银行体系合并资产负债表 一般来说,剔除个别特殊业务情况,可以将中央银行和商业银行的资产负债 表进行合并如下表10-1所示。 表10-1 银行合并资产负债表 资产(ASSETS) 负债(LIABILITIES) Aa 各项贷款 La 储蓄及定期存款 A 财政借款 L 财政存款 A 在国际货币基金组织中的资产 L. 国际金融机构往来 A 黄金外汇存款 La 银行资本及其他 M 现金(M) 活期存款 根据会计核算原理,总资产=总负债,即: A+4+A+A=Lo+L+L+L+M 10-6 M=(An+A,+A+A)-(L。+L。+L.+La) 10-7 从式10-7可以看出,银行体系任何一项资产的增加都会引起M的增加:反
比例为 t ,非个人定期存款的准备金比率为 t r ,那么每一元活期存款中就会有 t t r 作为法定准备金从存款派生体系中漏出,那么根据上述 10-1 式原理,从而派生 存款乘数进一步扩展为: 1 ' d t K r c g t r = + + + 10-5 第三节 货币供应的理论模型 一、货币供给与银行体系的合并资产负债表 货币供给与银行体系的资产负债业务有着密切的关系,因为,流通中的现金 是中央银行对大众的负债;银行存款又是商业银行对存款部门的负债。通过分析 银行机构的资产负债的关系而揭示货币供给的决定因素。 (一)银行体系合并资产负债表 一般来说,剔除个别特殊业务情况,可以将中央银行和商业银行的资产负债 表进行合并如下表 10-1 所示。 表 10-1 银行合并资产负债表 资产(ASSETS) 负债(LIABILITIES) A a 各项贷款 Ab 财政借款 A c 在国际货币基金组织中的资产 Ad 黄金外汇存款 L a 储蓄及定期存款 Lb 财政存款 L c 国际金融机构往来 Ld 银行资本及其他 M1 现金( M1 ) 活期存款 根据会计核算原理,总资产=总负债,即: A A A A L L L L M a b c d a b c d + + + = + + + + 1 10-6 M A A A A L L L L 1 = + + + − + + + ( a b c d a b c d ) ( ) 10-7 从式 10-7 可以看出,银行体系任何一项资产的增加都会引起 M1 的增加;反