德布罗意波的实验验证 1、戴维逊-革末实验 戴维逊和革末的实验是用电子束垂直投射到镍单晶,电子束被 散射。其强度分布可用德布罗意关系和衍射理论给以解释,从 而验证了物质波的存在。1937年他们与G.P.汤姆孙一起获得 Nobel物理学奖。 K 实验装置: 电子从灯丝K飞出,经电势 差为U的加速电场,通过狭 缝后成为很细的电子束,投 射到晶体M上,散射后进入 电子探测器,由电流计G测 量出电流。 M
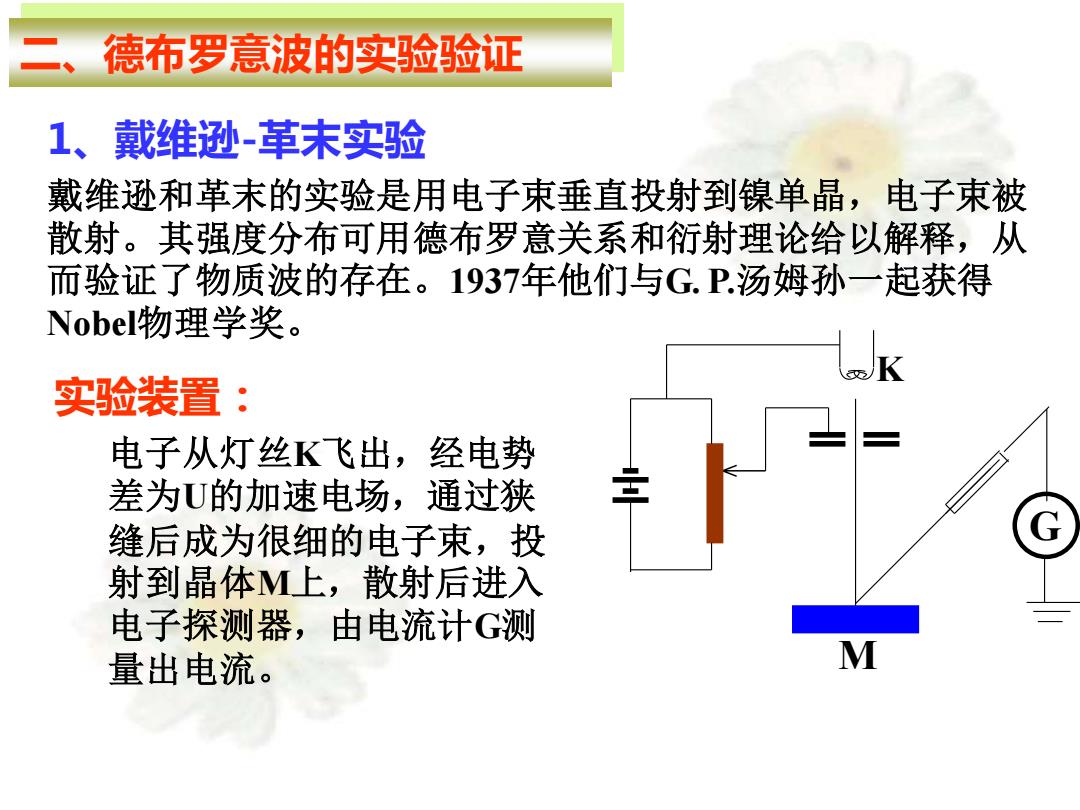
二、德布罗意波的实验验证 1、戴维逊-革末实验 G M K 戴维逊和革末的实验是用电子束垂直投射到镍单晶,电子束被 散射。其强度分布可用德布罗意关系和衍射理论给以解释,从 而验证了物质波的存在。1937年他们与G. P.汤姆孙一起获得 Nobel物理学奖。 实验装置: 电子从灯丝K飞出,经电势 差为U的加速电场,通过狭 缝后成为很细的电子束,投 射到晶体M上,散射后进入 电子探测器,由电流计G测 量出电流
实验现象: 实验发现,单调地增加加速电压, 电子探测器的电流并不是单调地增 加的,而是出现明显的选择性。例 如,只有在加速电压U=54V,且 0=50时,探测器中的电流才有极 54 U(V) 大值。 实验解释: 2A=2dsin号cos日=ka 2 @121 dsina=kA 当加速电压U=54V,加速电子的能量 eU=w2/2,电子的德布罗意波长为 h =16.7nm p 2meU
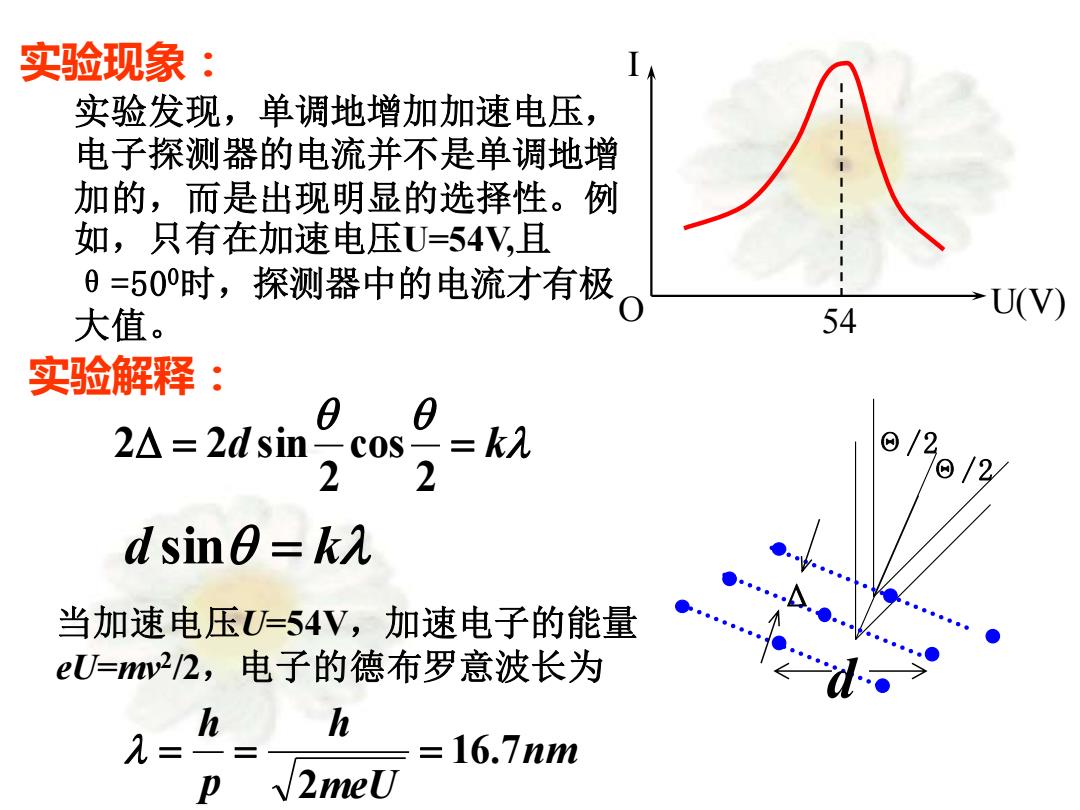
实验现象: 实验发现,单调地增加加速电压, 电子探测器的电流并不是单调地增 加的,而是出现明显的选择性。例 如,只有在加速电压U=54V,且 θ=500时,探测器中的电流才有极 大值。 Θ/2 Θ/2 d l = d = k 2 cos 2 2 2 sin Δ d sin = kl 实验解释: 当加速电压U=54V,加速电子的能量 eU=mv2 /2,电子的德布罗意波长为 nm meU h p h 16.7 2 l = = = 54 U(V) I O

kh dsine= √2meU kh 1 sin0 d 2meU X射线实验测得镍单晶的晶格常数d=0.215nm ar℃sinθ=0.777 0=arcsin0.777=51° 实验结果: 理论值(0=50)与实验结果(0=51)相差很小,表明电子电子 确实具有波动性,德布罗意关于实物具有波动性的假设是正确 的
meU kh d 2 sin = X射线实验测得镍单晶的晶格常数d=0.215nm arcsin = 0.777 实验结果: 理论值(θ=500 )与实验结果(θ=510 )相差很小,表明电子电子 确实具有波动性,德布罗意关于实物具有波动性的假设是正确 的。 d meU kh 2 1 sin = o = arcsin 0.777 = 51

2、汤姆逊实验 1927年,汤姆逊在实验中,让电子束 通过薄金属笛后射到照相底线上,结 果发现,与X射线通过金箔时一样, 也产生了清晰的电子衍射图样。 1993年,Crommie等人用扫描隧道显微 镜技术,把蒸发到铜(111)表面上的 铁原子排列成半径为7.13nm的圆环形 量子围栏,用实验观测到了在围栏内形 成的同心圆状的驻波(“量子围栏”), 直观地证实了电子的波动性。 3、电子通过狭缝的衍射实验: 1961年,约恩孙(Jonsson)制成长为50μm,宽为0.3μm,缝间 距为1.0μm的多缝。用50V的加速电压加速电子,使电子束分 别通过单缝、双缝等,均得到衍射图样
2、汤姆逊实验 1927年,汤姆逊在实验中,让电子束 通过薄金属笛后射到照相底线上,结 果发现,与X射线通过金箔时一样, 也产生了清晰的电子衍射图样。 1993年,Crommie等人用扫描隧道显微 镜技术,把蒸发到铜(111)表面上的 铁原子排列成半径为7.13nm的圆环形 量子围栏,用实验观测到了在围栏内形 成的同心圆状的驻波(“量子围栏”), 直观地证实了电子的波动性。 3、电子通过狭缝的衍射实验: 1961年,约恩孙(Jonsson)制成长为50mm,宽为0.3mm ,缝间 距为1.0mm的多缝。用50V的加速电压加速电子,使电子束分 别通过单缝、双缝等,均得到衍射图样

皂子衡谢 玉光行射