
二、相关图 可通过Excel绘制相关图(散点图) 三、相关系数(直线积差相关系数) 相关系数可以测定变量之间相关的密切程度。 (一)原始公式及判断标准 1、原始公式 y=-xy-) Noxay 它是著名英国统计学家卡尔.皮尔逊设计的。 重慶上商大学 制作:赵镜学院,黄应伦
制作:数统学院 . 黄应绘 二、相关图 可通过Excel绘制相关图(散点图)。 三、相关系数(直线积差相关系数 ) 相关系数可以测定变量之间相关的密切程度。 (一)原始公式及判断标准 1、原始公式 ( )( ) N x y x x y y r − − = 它是著名英国统计学家卡尔.皮尔逊设计的
0 为了研究父亲与成年儿子 身高之间的关系,卡尔皮 尔逊测量了1078对父子的 身高。把1078对数字表示 在坐标上,如图。用水平 轴X上的数代表父亲身高, 垂直轴Y上的数代表儿子 的身高,1078个点所形成 的图形是一个散点图。它 的形状象一块橄榄状的云, 中间的点密集,边沿的点 稀少,其主要部分是一个 椭圆。 父的身献英) 重度工商大学 制作:镜计学院黄应管
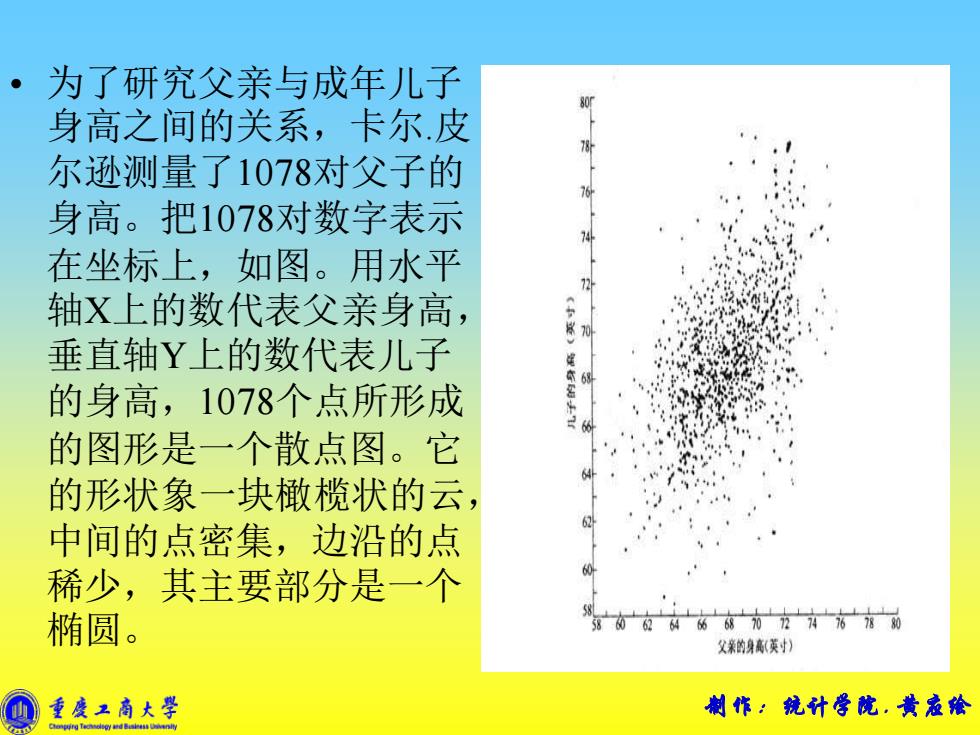
• 为了研究父亲与成年儿子 身高之间的关系,卡尔 . 皮 尔逊测量了1078对父子的 身高。把1078对数字表示 在坐标上,如图。用水平 轴X上的数代表父亲身高, 垂直轴 Y上的数代表儿子 的身高,1078个点所形成 的图形是一个散点图。它 的形状象一块橄榄状的云, 中间的点密集,边沿的点 稀少,其主要部分是一个 椭圆。 制作:统计学院. 黄应绘

以上公式中,除去Ox、oy,剩下的 叫做x与y的协方差,用CoV或σ品表示。 2 所以,Y= 重度工商大学 制作:数就骨院,黄应食
制作:数统学院 . 黄应绘 以上公式中,除去 、 ,剩下的 叫做x与y的协方差,用COV或 表示。 x y 2 xy 所以 , x y xy 2 =

2、判断标准 1)相关系数的取值范围在-1至1之间。 其绝对值大小反映两变量之间相关的密切程度, (2)相关系数有正负号,分别表示正相关和负相关。 (3)相关系数=1表明两变量完全直线相关; y=0表明两变量不存在直线相关; 3、习题:试证明完全正直线相关时,r等于1; 完全负直线相关时,r等于-1。 制作,数镜学院,黄应徐
制作:数统学院 . 黄应绘 2、判断标准 (1)相关系数的取值范围在-1至1 之间。 其绝对值大小反映两变量之间相关的密切程度, (2)相关系数有正负号,分别表示正相关和负相关。 (3)相关系数 = 1 表明两变量完全直线相关; = 0 表明两变量不存在直线相关; 3、习题:试证明完全正直线相关时,r等于1; 完全负直线相关时,r等于-1

(二)常用计算公式 n∑xy-∑x∑y -(xj-明 Q 重度工商大学 制作;数镜学院,黄应徐
制作:数统学院 . 黄应绘 ( ) ( ) − − − = n x x n y y n x y x y 2 2 2 2 (二)常用计算公式