
Crystallography Leyun Wang School of Materials Science and Engineering, SJTU leyunwang@sjtu.edu.cn 1
Crystallography Leyun Wang School of Materials Science and Engineering, SJTU leyunwang@sjtu.edu.cn 1
Crystallography ·Crystal systems and Bravais lattices(晶 系与布拉维点阵) 影 ·Point group and space group(点群 与空间群) 。Reciprocal lattice (倒易点阵)
Crystallography • Crystal systems and Bravais lattices ( 晶 系与布拉维点阵 ) • Point group and space group (点群 与空间群 ) • Reciprocal lattice (倒易点阵 ) 2
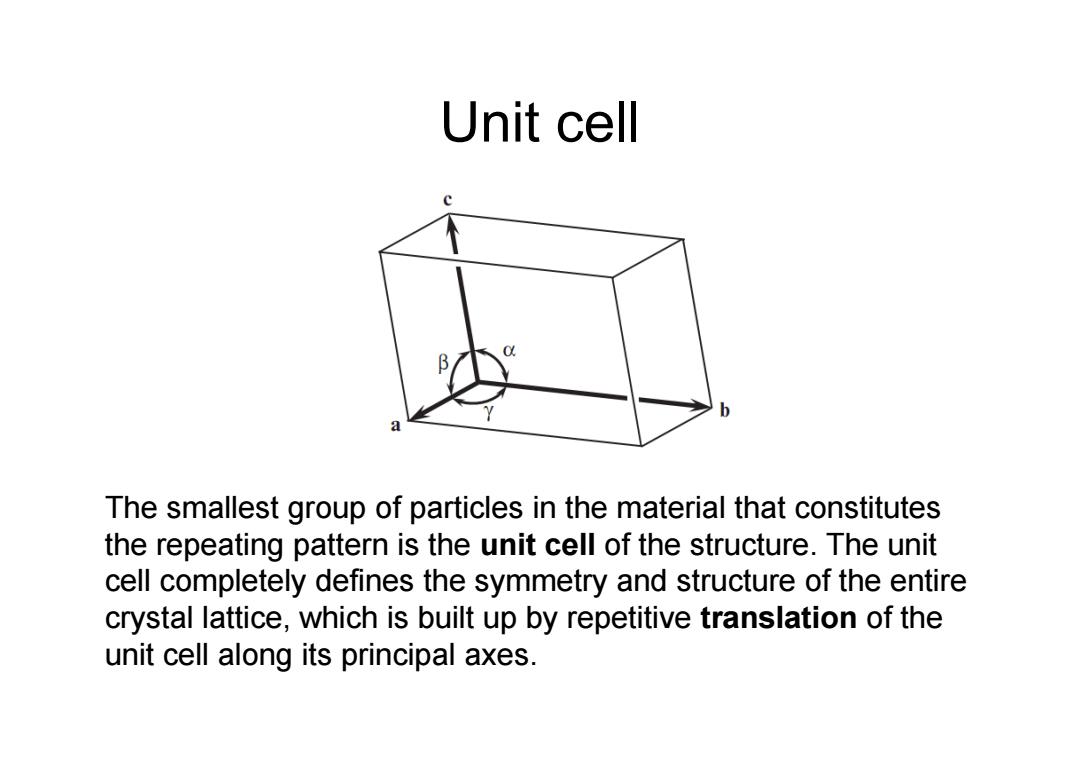
Unit cell a The smallest group of particles in the material that constitutes the repeating pattern is the unit cell of the structure.The unit cell completely defines the symmetry and structure of the entire crystal lattice,which is built up by repetitive translation of the unit cell along its principal axes
Unit cell The smallest group of particles in the material that constitutes the repeating pattern is the unit cell of the structure. The unit cell completely defines the symmetry and structure of the entire crystal lattice, which is built up by repetitive translation of the unit cell along its principal axes
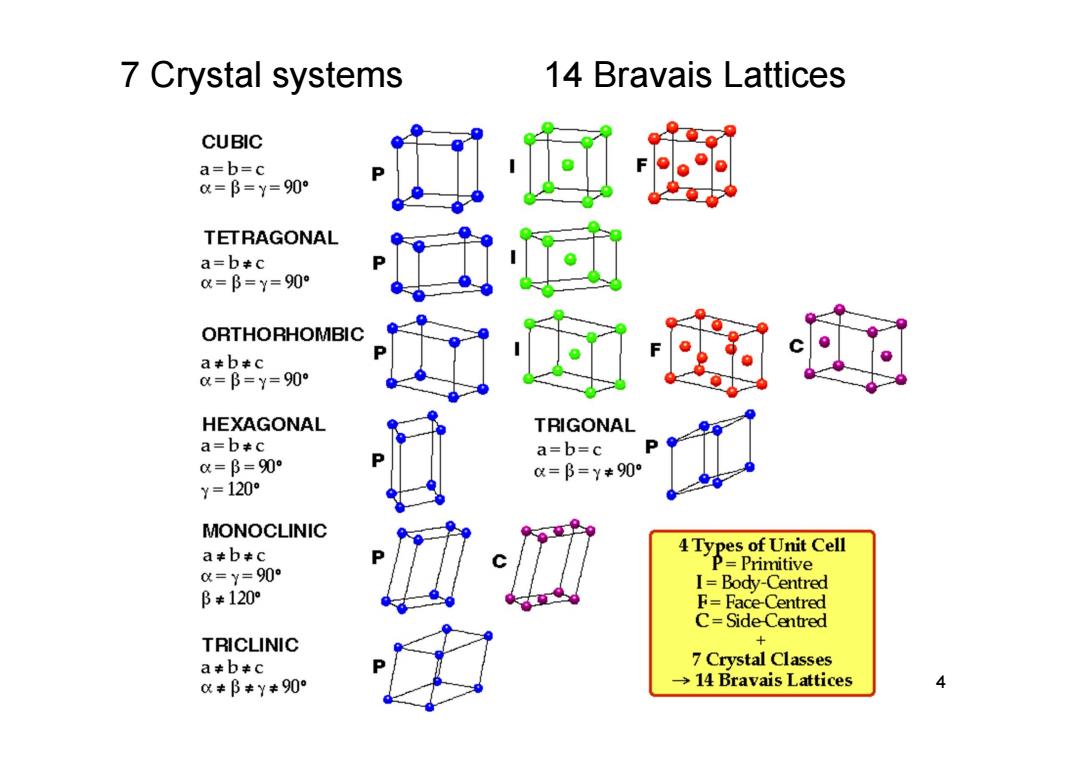
7 Crystal systems 14 Bravais Lattices CUBIC a=b=c =B=y=90° TETRAGONAL a=b+c =B=y=90° ORTHORHOMBIC a+b+c &=B=y=90° HEXAGONAL TRIGONAL a=btc a=b=c =B=90° =B=y*90° y=120° MONOCLINIC atb#c 4 Types of Unit Cell P=Primitive =y=90° I=Body-Centred B*120° F=Face-Centred C=Side Centred TRICLINIC a+b+c 7 Crystal Classes *阝*y*90° →14 Bravais Lattices 4
4 7 Crystal systems 14 Bravais Lattices
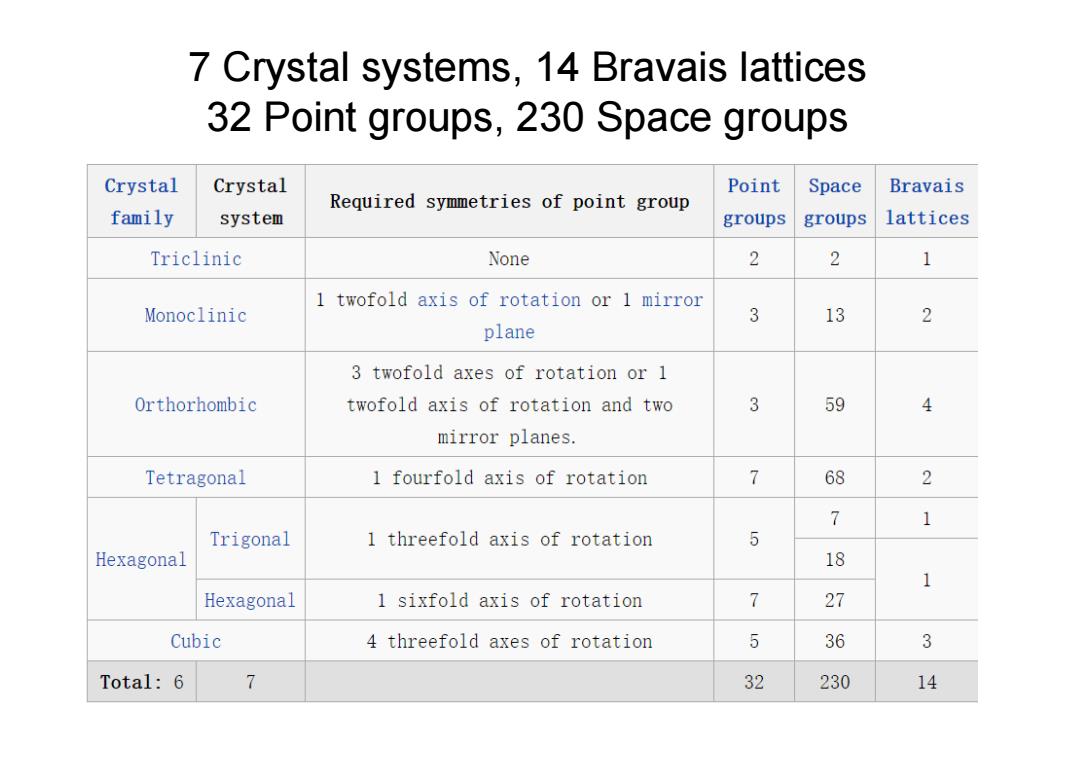
7 Crystal systems,14 Bravais lattices 32 Point groups,230 Space groups Crystal Crystal Point Space Bravais Required symmetries of point group family system groups groups lattices Triclinic None 2 2 1 1 twofold axis of rotation or 1 mirror Monoclinic 3 13 2 plane 3 twofold axes of rotation or 1 Orthorhombic twofold axis of rotation and two 3 59 4 mirror planes. Tetragonal 1 fourfold axis of rotation 7 68 2 7 1 Trigonal 1 threefold axis of rotation 5 Hexagonal 18 1 Hexagonal 1 sixfold axis of rotation 7 27 Cubic 4 threefold axes of rotation 5 36 3 Total:6 7 32 230 14
5 7 Crystal systems, 14 Bravais lattices 32 Point groups, 230 Space groups