
第一章 量子论基础 §1.1经典物理学的困难 19世纪末20世纪初,经典物理学,主要是经典力学、热力学和 经典统计物理学、经典电动力学,已经发展得相当完善。比方,速度 远小于光速的物体的机械运动遵从牛顿力学规律:电磁现象满足 麦克斯韦方程;光的现象有光的波动理论;特别是当时已认识到热 辐射和光辐射都是电磁波,还提出了热辐射满足的基尔霍夫(G. Kirchhoff)定律和斯忒藩(J.Stefan)定律,证实黑体辐射场的能 量密度与温度的四次方成正比。对于热现象,除了已经有了非常系 统的热力学理论外,还有玻耳兹曼、吉布斯等人提出的统计物理 学。经典物理学的大厦已经建立得相当完美了。 但是,在和实验进一步对比的过程中,也出现了一些困难,而 且这些困难,在经典物理的范畴内是无法解释的。这主要表现在: 1.黑体辐射“ 任何物体总在吸收投射在它身上的辐射,物体吸收的辐射能 量与投射到物体上的辐射能之比称为该物体的吸收系数。一般地, 物体只吸收投射到它表面上的部分能量,吸收系数小于1。如果一 个物体,能吸收投射到它表面上的全部辐射,即其吸收系数为1 时,则称这个物体为绝对黑体,简称黑体。一个开有一个小孔的空 腔可近似视为黑体。因为一旦光线通过小孔射入空腔后,就很难再 通过小孔反射出来。 ·关于黑体辆射和比热的详细论述可参阅苏妆锋:《统计物理学》,复旦大学出版 杜,1990.54.1,§4.2,§4.5,S4.6
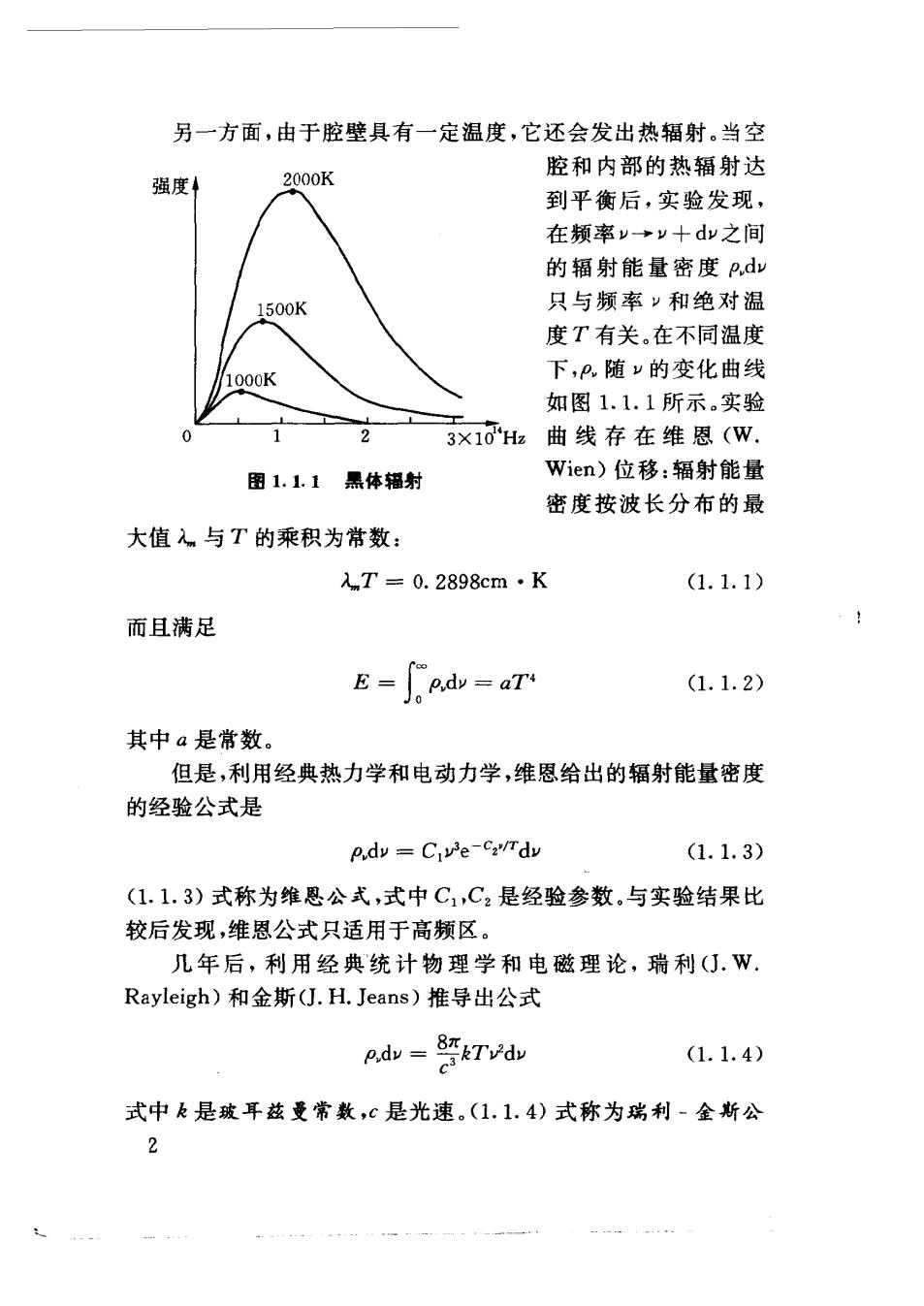
另一方面,由于腔壁具有一定温度,它还会发出热辐射。当空 腔和内部的热辐射达 强度 2000K 到平衡后,实验发现, 在频率y→y十dy之间 的辐射能量密度p,dy 1500K 只与频率”和绝对温 度T有关。在不同温度 000K 下,A随y的变化曲线 如图1.1.1所示.实验 3×10Hz曲线存在维恩(W. 图1.1.1黑体辐射 Wien)位移:辐射能量 密度按波长分布的最 大值入与T的乘积为常数: 入T=0.2898cm·K (1.1.1) 而且满足 E-Sedv-aT (1.1.2) 其中a是常数。 但是,利用经典热力学和电动力学,维恩给出的辐射能量密度 的经验公式是 pdy =Cve-C:Tdv (1.1.3) (1.1.3)式称为维恩公式,式中C1,C2是经验参数.与实验结果比 较后发现,维恩公式只适用于高频区。 几年后,利用经典统计物理学和电磁理论,瑞利(J.W. Rayleigh)和金斯(J.H.Jeans)推导出公式 e.dv=8Tvdv (1.1.4) 式中k是玻耳兹曼常数,c是光速。(1.1.4)式称为瑞利-金斯公 2

式。它只在低频区与实验相符.在高频区,当y→∞时,P.→∞,而 且能量密度发散, E=∫pdw=8STdy→∞ (1.1.5) 这个结果称为来外灾难。 2光电效应 1888年,赫兹(H.Hertz)在验证电磁波存在的实验中,发现当 用紫外光照到火花隙的负极上时,放电比较容易发生。1897年汤 姆孙(J.J.Thomson)通过气体放电和阴极射线的研究发现电子 后,人们逐渐认识到这种现象是由于紫外光照射到金属表面上,金 属中的电子吸收了光的能量而从金属表面逸出所至,这种逸出的 电子称为光电子。对于表面光洁的金属材料,光电效应的实验结果 是: ()存在临界频率%,当入射光的频率”<%时,无论光的强 度多大,都无光电子逸出。只有在y≥“时,即使光的强度较弱,但 只要光照到金属表面上,几乎在10~s的极短时间内,就能观测到 光电子。 (i)出射的光电子的能量只与入射光的频率”有关,而与入 射光的强度无关。 ()入射光的强度只影响光电流的强弱,即只影响在单位时 间内由单位面积上逸出的光电子的数目。 显然,这些实验结果,特别是()和(),无法用经典电磁理论 解释。因为按经典电动力学,光是电磁波。电磁波的能量决定于它 的强度,即只与电磁波的振幅有关,而与电磁波的频率无关。而要 释放光电子,显然需要有足够的能量。 3.原子的线状光谱 1885年,巴耳末(J.J.Balmer)通过对氢的光谱线分析研究 后,发现氢原子可见光的光谱线满足经验公式 立=是==R是-m=34,5…11.6) 3

v为波长的倒数,称为波数。Ra称为里德伯(J.R.Rydberg)常数, 数值上等于109677.581cml。以后又陆续发现了其他线系,1889 年,里德伯把氢的所有谱线归纳为一个里德伯方程,即 =文=R[是-]=T)-Tm)a.) 式中,n=1,2,3,…:对于每一个n,有n=n+1,n十2,n十3,… 构成一个谱线系。T(n)称为光谱项。由(1.1.7)式可见,如果光谱 中有频率为4和的两条谱线,则也有频率为”十及山一“2】 的谱线。这个结果称为里兹(W.Ritz)的并合原则。 原子的线状光谱用经典理论也是无法解释的,因为按卢瑟福 模型,原子中电子绕原子核运动。这是一种加速运动。但按经典电 动力学,加速电荷应不断发出辐射。于是电子不断损失能量,而且, 加速电荷发出的辐射的频率是连续分布的,不可能产生线状光谱 此外,按电动力学,若体系发出频率为的波,则它也可能发出频 率为的整数倍的其他谐波。这个结论也与并合原则不符。 4.原子的稳定性 原子结构的卢瑟福模型在经典理论中是无法理解的。因为电 子既然绕原子核运动,则在这一加速运动过程中,由于辐射能量, 必然使电子绕核运动的轨道变小。最后“落到”原子核中去。也就 是说,按经典理论,卢瑟福的原子模型是不稳定的。这种原子最后 必然坍缩成一团。但是现实世界中原子是稳定的。经典理论无法解 释这个实验事实。 5.比 热 经典统计物理的比热理论建立在能量均分定理的基础上。在 和实验比较后发现,经典的比热理论存在着下述困难: (i)固体比热的杜隆-珀蒂(Dulong-Petit)定律 Cp≈Cv=3R (1.1.8) 只在常温下与实验相符,在极低温下,固体比热服从德拜(P.Debye) T3定律:Cp与T3成正比。 4

()不能解释为什么原子中处于束缚态的电子对比热的贡 献可以略去。因为按原子模型,原子核外的电子在运动,而按能量 均分定理,每个电子运动的平均动能为号T,相应的定容比热应 为。 ()不能解释为什么绝大部分双原子分子,多原子分子在常 温下振动自由度被冻结,对比热没有贡献。 除了当时已出现的这些困难外,1923年发现的康善频(A.H. Compton)效应,也不能用经典理论解释.实验发现,高频率的X射 线被轻元素的电子散射后,散射波的波长随散射角的增大而增大 这个结果也无法用经典理论说明,因为散射过程只涉及入射光与 电子之间的能量和动量交换,而按经典理论,电磁波的能量只与振 幅有关,而与波长无关,能量、动量的交换不应导致波长的变化。 对于经典物理学的这些困难,19世纪的许多有为的物理学 家,其实是早有察觉,忧虑重重的。1859年,气体分子运动论的奠 基人之一麦克斯韦,就明确指出了经典比热理论的困难。十年后, 他又重复强调了这个困难,并且指出这里存在着一些经典物理根 本不可能解释的东西。以后,金斯等人又作过许多讨论。正是麦克 斯韦等人的这些真知灼见,使得美国著名物理学家费曼(R.P. Feymann)得以有根据地说:“人们经常听说19世纪后期的物理学 家认为,他们已经了解了所有有意义的物理规律,因而以后所能作 的只是去计算更多的小数位.某个人可能这么说过一次,其他人就 争相传抄,但是彻底查阅当时的文献表明,他们所有的人都是对某 些问题忧虑重重的。”①正是因为当时这些有为的物理学家们,根 本不像有些人所说的那样,躺倒在经典物理学的大厦里恬然自得, 以为已经最后解决了一切物理学问题恰恰相反,他们多年如一日 地深入思考着经典物理学的困难,不固步自封,勇于进取,寻找解 ①费曼,莱登,桑兹:《费曼物理学讲义》第一卷,上海科学技术出版社,1978.第 398 5