上讲回顾 500根钢棒的长度服从正态分布。其均值为11cm,标准偏 差为1cm。试估计长度大于13cm的钢棒的数量. 先进行标准化变换: 1.6 9452 9463 9474 .9484 13.0-11.0 2 1.7 9554 9564 9573 9582 1.8 9641 .9648 .9656 .9664 1.9 9713 .9719 9726 .9732 F(2)=0.9772 2.0 .9772 .9778 9783 .9788 于是,500*(1-0.9772)=11 2.1 9821 9826 9830 9834 根钢棒的长度大于13cm 2.2 9861 .9864 9868 .9871 2.3 9893 .9896 .9898 .9901 2.4 9918 .9920 .9922 .9924 2.5 .9938 .9940 .9941 .9943 11
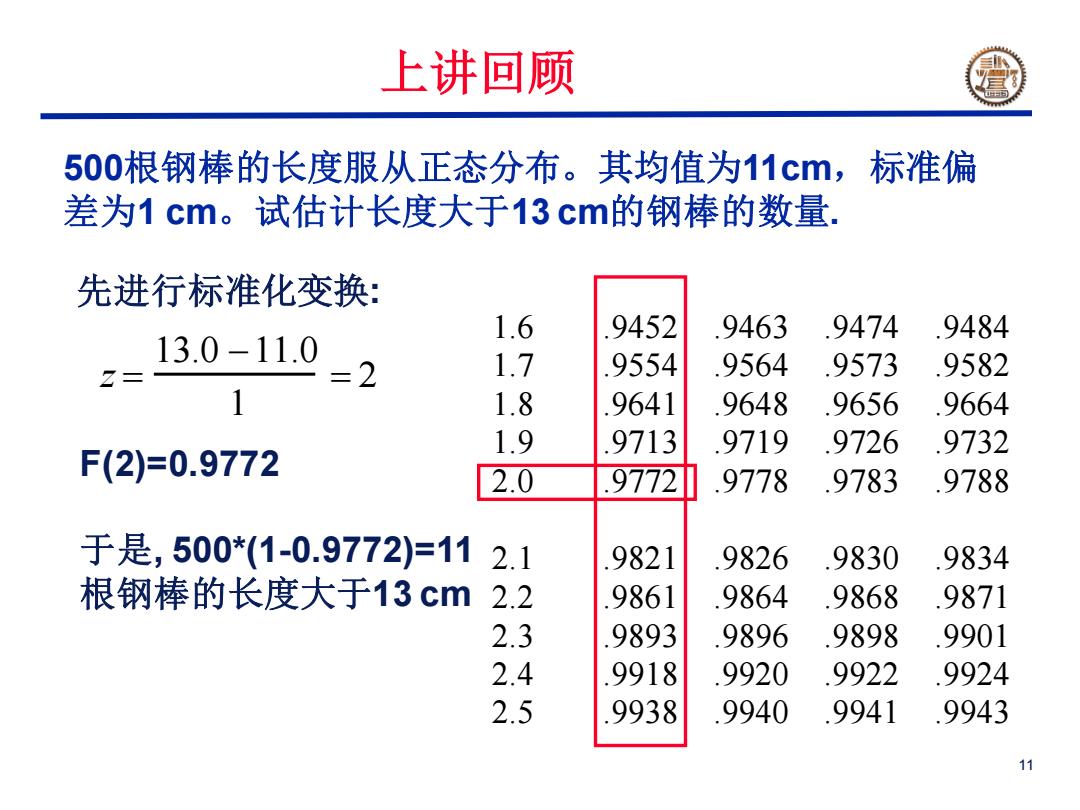
11 500根钢棒的长度服从正态分布。其均值为11cm,标准偏 差为1 cm。试估计长度大于13 cm的钢棒的数量. z 13.0 11.0 1 2 F(2)=0.9772 于是, 500*(1-0.9772)=11 根钢棒的长度大于13 cm 1.6 .9452 .9463 .9474 .9484 1.7 .9554 .9564 .9573 .9582 1.8 .9641 .9648 .9656 .9664 1.9 .9713 .9719 .9726 .9732 2.0 .9772 .9778 .9783 .9788 2.1 .9821 .9826 .9830 .9834 2.2 .9861 .9864 .9868 .9871 2.3 .9893 .9896 .9898 .9901 2.4 .9918 .9920 .9922 .9924 2.5 .9938 .9940 .9941 .9943 先进行标准化变换: 上讲回顾

复合统计 ■假定有两组数据,我们要对两组数据进行复合统计。 ■例如,两个相互配合的零件的配合尺寸数据;或者承 载零件的强度与加载零件的加载力之间的关系。 如果零件的尺寸、强度或应力有变化,则原本能够配 合的两个零件可能配合不上,承载零件可能失效断裂 等。 从均值的定义可以看出,均值可以进行加减运算。 12
12 复合统计 假定有两组数据,我们要对两组数据进行复合统计。 例如,两个相互配合的零件的配合尺寸数据;或者承 载零件的强度与加载零件的加载力之间的关系。 如果零件的尺寸、强度或应力有变化, 则原本能够配 合的两个零件可能配合不上,承载零件可能失效断裂 等。 从均值的定义可以看出,均值可以进行加减运算

复合统计 从一列数据中分别随机挑出x1,x2,x3,.和y1,y2,y3,… 做加法: z1=x1+y1,z2=x2+y2,etc. 或减法 z1=x1-y1,z2=x2-y2,etc. 均值的计算如下: =Σ2x+w ∑±∑=±5 13
13 从一列数据中分别随机挑出 x1, x2, x3,... 和y1, y2, y3,… 做加法: z1=x1+y1, z2=x2+y2, etc. 或减法 z1=x1-y1, z2=x2-y2, etc. 均值的计算如下: z 1 N zi i 1 N xi i 1 N yi i 1 N (xi yi ) i x y 复合统计

复合统计 方差为: =双2-户N26±5-61g月 Σ-x)生6-y万 NΣ医-x)+6-y±26近》 对于独立或 无关联变量 14
14 方差为: sz 2 1 N 1 (z zi i ) 2 1 N 1 x y xi yi 2 i 1 N 1 x xi 2 y yi 2 2 x xi y yi i sx 2 sy 2 0 1 N 1 (x xi ) (y yi ) 2 i 对于独立或 无关联变量 复合统计

复合统计 对于连续分布,均值也能相加减: 4。=山1+42 或 4。=41一2 方差必须相加: o,af +o? 标准偏差为: 0。=0+o 15
15 o 1 2 o 1 2 o 2 1 2 2 2 o 1 2 2 2 对于连续分布,均值也能相加减: 方差必须相加: 标准偏差为: 或 复合统计