电子科技大学：《计算电磁学 Computational Electronmagentics》课程教学资源（课件讲稿，有限差分法）第4章 时域有限差分法 I 4.1 FDTD基本原理 4.2 解的稳定性条件 4.3 非均匀网格 4.4 共形网格 4.5 半解析数值模型 4.6 良导体中的差分格式

计算电磁学（小班研讨课) 966 第4章时域有限差分法I 4.1FDTD基本原理 4.2解的稳定性条件 目录 4.3非均匀网格 4.4共形网格 4.5半解析数值模型 4.6良导体中的差分格式 2

2 计算电磁学（小班研讨课） 目 录 第4章 时域有限差分法 I 4.1 FDTD基本原理 4.2 解的稳定性条件 4.3 非均匀网格 4.4 共形网格 4.5 半解析数值模型 4.6 良导体中的差分格式

计算电磁学 966 第4章时域有限差分法I 差分格式及解的稳定性 3

3 第4章 时域有限差分法 I ——差分格式及解的稳定性 计算电磁学

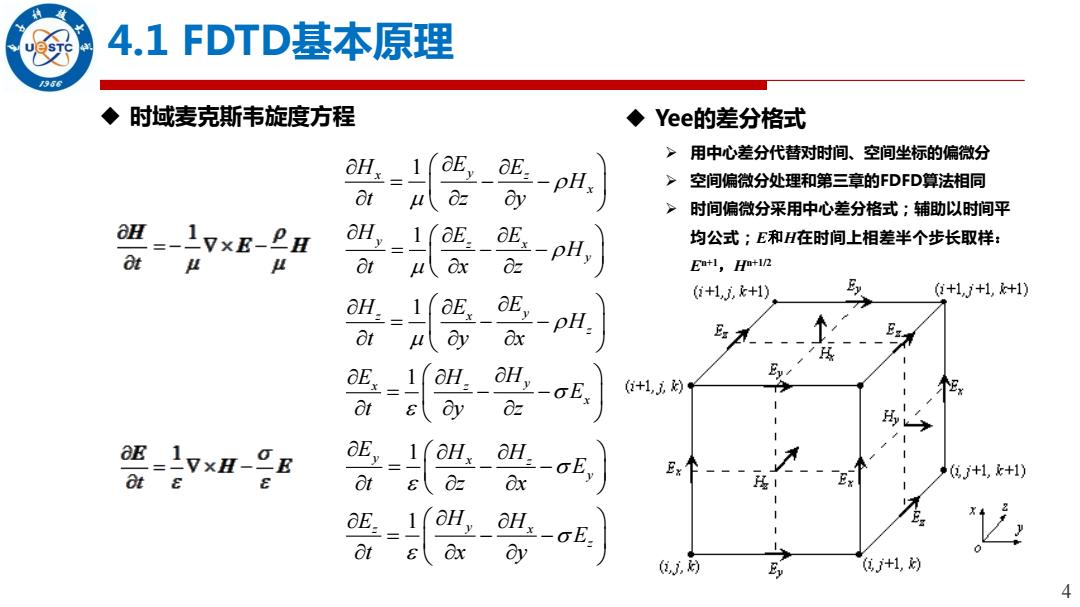
4.1FDTD基本原理 956 ◆时域麦克斯韦旋度方程 ◆Yee的差分格式 OH,1(E, > 用中心差分代替对时间、空间坐标的偏微分 OE. 空间偏微分处理和第三章的FDFD算法相同 8t uz 8y -pH: 时间偏微分采用中心差分格式；辅助以时间平 =-1vxB-PH OH,1(E. aE, 均公式：E和H在时间上相差半个步长取样： 4 u at u Ox 8z -pHy En+l,Ha+in2 (+1,,k+1) E (+1j+1,+1) OH.1(E, E, 8t u by Ox -pH. E:7 盟 H _-oE: +1,) ot dy 02 E,1(OH.OH. Ex Ot s Oz Ox g+1,k+1) Ot Ox 0H.-cE. Cy (,) +1， 4

4 4.1 FDTD基本原理  时域麦克斯韦旋度方程 z 1 x y z H E E H t y x                  x 1 y z x H E E H t z y                  y 1 z x y H E E H t x z                  x 1 z y x E H H E t y z                  y 1 x z y E H H E t z x                  z 1 y x z E H H E t x y                   Yee的差分格式  用中心差分代替对时间、空间坐标的偏微分  空间偏微分处理和第三章的FDFD算法相同  时间偏微分采用中心差分格式；辅助以时间平 均公式；E和H在时间上相差半个步长取样： En+1，Hn+1/2

4.1FDTD基本原理 ◆Yee的差分格式 >Hx展开点(n△t,ix,G+1/2)△y.(k+1/2)△z)→(4.10) ++-c4++rc △ >Hy展开点(nAt,(i+1/2)△x,jy,(k+1/2)△z)→(4.11) …且外 △x >Hz展开点（nAt,(i+1/2)△x,0+1/2)Ay,k△z)→(4.12) cfc5o-eu 5

5 4.1 FDTD基本原理  Yee的差分格式  Hx展开点（nt, ix, (j+1/2)y, (k+1/2)z）(4.10)  Hy展开点（nt, (i+1/2)x, jy, (k+1/2)z）(4.11)  Hz展开点（nt, (i+1/2)x, (j+1/2)y,kz）(4.12) 1 1 2 2 ,1 ,2 1 1 1 1 , , 1 , , , , , 1, 1 1 1 1 2 2 2 2 , , , , +C 2 2 2 2 n n n n y y z z n n x Hx x Hx E i j k E i j k E i j k E i j k H i j k C H i j k z y                                                                   1 1 2 2 ,1 ,2 1 1 1 1 1, , , , , , , , 1 1 1 1 1 2 2 2 2 , , , , 2 2 2 2 n n n n z z x x n n y Hy y Hy E i j k E i j k E i j k E i j k H i j k C H i j k C x z                                                                    1 1 2 2 ,1 ,2 1 1 1 1 , 1, , , , , 1, , 1 1 1 1 2 2 2 2 , , , , 2 2 2 2 n n n n x x y y n n z Hz z Hz E i j k E i j k E i j k E i j k H i j k C H i j k C y x                                                                   

4.1FDTD基本原理 ◆Yee的差分格式 Ex展开点((n+1/2)At(i+1/2)△x,jy,k)→(4.13) f-c小a >y展开点(n+1At,iax0+1/2)△y.k△z)→(4.14) 小时L“ro封 >Ez展开点((n+1/2)△t,ix,j4y.(k+1/2)△z)→(4.15) ea听ua生 6

6 4.1 FDTD基本原理  Yee的差分格式  Ex展开点（(n+1/2)t, (i+1/2)x, jy, kz） (4.13)  Ey展开点（(n+1/)t, ix, (j+1/2)y, kz） (4.14)  Ez展开点（(n+1/2)t, ix, jy,(k+1/2)z） (4.15) 1 1 1 1 2 2 2 2 1 ,1 ,2 1 1 1 1 1 1 1 1 , , , , , , , , 1 1 2 2 2 2 2 2 2 2 , , , , + 2 2 n n n n z z y y n n x Ex x Ex H i j k H i j k H i j k H i j k E i j k C E i j k C y z                                                                      1 1 1 1 2 2 2 2 1 ,1 ,2 1 1 1 1 1 1 1 1 , , , , , , , , 1 1 2 2 2 2 2 2 2 2 , , , , + 2 2 n n n n x x z z n n y Ey y Ey H i j k H i j k H i j k H i j k E i j k C E i j k C z x                                                                      1 1 1 1 2 2 2 2 1 ,1 ,2 1 1 1 1 1 1 1 1 , , , , , , , , 1 1 2 2 2 2 2 2 2 2 , , , , + 2 2 n n n n y y x x n n z Ez z Ez H i j k H i j k H i j k H i j k E i j k C E i j k C x y                                                                     