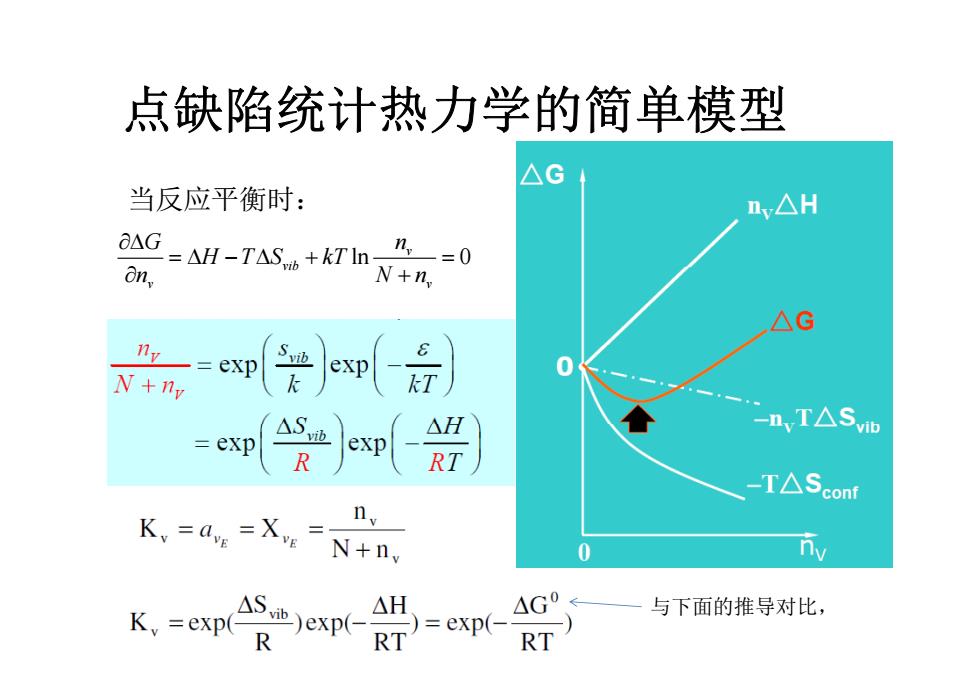
点缺陷统计热力学的简单模型 △G 当反应平衡时: nv△H OAG -AH-TAS+kT'In0 on, N+n AG exp S vib exp 0 N+ny kT △S △H -n,T△Sv =exp exp R RT -T△Sconf Ky=dv=Xv=N+ny 0 S)exp( K,=exp(R △H )=exp(- G0 与下面的推导对比, RT RT
点缺陷统计热力学的简单模型 当反应平衡时: ln 0 v vib G n H T S kT N vib v v n N n 与下面的推导对比

从化学反应角度讨论缺陷反应 一点回顾: G 在一个多组分系统中,化学势定义: 4=( )1,pnh 那么整个系统的自由能为:G=n4,+n242+n,4 由于组分变化造成的自由能变化:dGr,p=4,dn+42dn2+4, 系统平衡时:dG.p=∑4,dm,=0 对于一个反应: aA+bB=cC+dD 反应后自由能变化为:AG=cIc+dwo-(aWA+hB) 化学势可被写为:4,=u+RT In a 理想溶液:a,=X, 非理想溶液:a,=y,X, 因此可以得到: AG=AG°+RTIn aca2 axap
从化学反应角度讨论缺陷反应 一点回顾: 在一个多组分系统中,化学势定义: 那么整个系统的自由能为: 由于组分变化造成的自由能变化: 系统平衡时: 对于一个反应: 反应后自由能变化为: 化学势可被写为: 理想溶液: 非理想溶液: 因此可以得到:

从化学反应角度讨论缺陷反应 对于一个化学反应: aA+bB=cC +dD AG=△G°+RT1na吃af 当化学平衡时:∧G=0 acap △G=-RT In K K /equilibrium △G0=△H0-TAS0=-RTIn K K=K°exp-AH9 4.s )=exp RT R )exp(-AHo
从化学反应角度讨论缺陷反应 对于一个化学反应: 当化学平衡时: G=0

两种方法的结果对比 ·从化学反应的讨论我们得到 K=Kexp(- )=exp( RT R)exp(-4o )K°=exp(AsR) ·从统计热力学推导我们得到 .b)exp( K,=exp(R RT)=exp(-AG △H ·从上面的对比可以看到,K°=exp(△SR)只包含了振动熵 的贡献,不包括构型熵的贡献。 dInK_△H9 ·从上式可以看到:d1/T)R 如果对lnK和1/T画图, 截距为△SR,斜率为-△H/R
两种方法的结果对比 • 从化学反应的讨论我们得到 • 从统计热力学推导我们得到 • 从上面的对比可以看到, 只包含了振动熵 的贡献,不包括构型熵的贡献。 • 从上式可以看到: 如果对lnK 和1/T画图, 截距为 ,斜率为

需要注意的问题 ·在讨论化学平衡时某一组分的化学势的概念为在其他组分 不变(T、P也不变)的情况下的偏微分。对于缺陷反应, 我们知道反应前后格位的比例不变。即一种格位的产生和 消灭,会导致另一种格位的产生和消灭,上述条件难以满 足,即我们很难定义一种缺陷的化学势。 解决问题的方法是,定义一个表观化学势(virtual chemical potential) Si=5+RI Ina, 真正的化学势与表观化学势的差别包含在前面的系数°里 ,当计算总的自由能变化时,真正的化学势与表观化学势 的差别被抵消了。因此我们上述利用研究化学平衡的方法 研究缺陷反应是可行
需要注意的问题 • 在讨论化学平衡时某 在讨论化学平衡时某 组分的化学势的概念为在其他组分 一组分的化学势的概念为在其他组分 不变( T 、 P也不变)的情况下的偏微分。对于缺陷反应, 我们知道反应前后格位的比例不变。即一种格位的产生和 消灭,会导致另一种格位的产生和消灭,上述条件难以满 足,即我们很难定义一种缺陷的化学势。 • 解决问题的方法是,定义 个表观化学势 定义 一个表观化学势 (virtual chemical potential) 真正的化学势与表观化学势的差别包含在前面的系数 里 当计算总的自由能变化时 真正的化学势与表观化学势 0 i ,当计算总的自由能变化时,真正的化学势与表观化学势 的差别被抵消了。因此我们上述利用研究化学平衡的方法 研究缺陷反应是可行