
实验3-2-2脉冲波核磁共振 【实验目的】 1.理解脉冲波核磁共振的基本原理,掌握拉莫尔频率的测量方法。 2.理解纵向弛豫时间刀和横向弛豫时间万的物理意义,掌握测量T谱和谱的实验 方法和技术。 3.理解核磁共振成像的基本原理,学会磁共振成像的测量方法。 【预习要求】 1.什么是核磁共振?什么是脉冲波核磁共振? 2.发生核磁共振时,横向磁化强度矢量M如何改变? 3.90°和180°射频脉冲作用时,原子核的磁化强度矢量各如何改变? 4.如何根据磁化强度矢量的变化来测量核磁共振信号? 5.测量弛豫时间五和2各用什么方法? 6.怎样观测实验样品的核磁共振成像? 【实验原理】 一.脉冲核磁共振基本原理 1.脉冲改变核磁化强度状态 处于恒定磁场B(沿:轴方向)中的原子核自旋系统,其宏观磁化强度M以角频率 ,=B,绕B进动,垂直于B方向上施加一射频脉冲。在射频脉冲作用前,M处于热平 衡状态,方向与:轴重合:施加射频脉冲作用时,射频脉冲诱发两种能态间的原子核产生能 态跃迁,被激励的原子核从低能态跃迁到高能态,出现核磁共振。受到射频脉冲激励的原子 核的磁化强度M偏离原来的平衡状态而发生变化,其变化程达的位置度取决于所施加射频 脉冲的强度和时间。施加的射顷脉冲越强,持续时间越长,在射频脉种停止时,M离开其平 衡状态越远。在核磁共振成像技术中使用较多的是90°、180°射频脉冲。施加90°脉冲时,去 观磁化矢量M以螺旋运动的形式离开其原来的平衡状态,脉冲停止时,M垂直于主磁场B, 如图3.2.10所示。 90°脉冲结束时,宏观磁化矢量M平行于y平面,纵向磁化矢量M=0,横向磁化 量M最大,如图32-11所示。这时质子群几乎以同样的相位旋进。施加180°脉冲后,M 与B0平行,但方向相反,横向磁化矢量M为零,如图3-212所示。 2核磁化强度的驰豫过程 脉冲停止后,M仍围绕B轴旋转,M末端螺旋上升逐渐靠向B,这个过程称之为“核 磁弛豫”。以90脉冲来说明射频脉冲停止后M的弛豫变化。如图3-213所示,在脉冲结来 的一瞬间,M在xy平面上分量M达最大值,在:轴上分量M为零。当恢复到平衡时,纵 向分量M重新出现,而横向分量M,消失。在弛豫过程中磁化矢量M强度并不恒定,故这 两个弛豫过程的特征分别用纵向地豫时间(longitudinal relaxation time)方和横向弛豫时间 (transverse relaxation time)T来描述
实验 3-2-2 脉冲波核磁共振 【实验目的】 1. 理解脉冲波核磁共振的基本原理,掌握拉莫尔频率的测量方法。 2. 理解纵向弛豫时间 T1 和横向弛豫时间 T2 的物理意义,掌握测量 T1 谱和 T2 谱的实验 方法和技术。 3. 理解核磁共振成像的基本原理,学会磁共振成像的测量方法。 【预习要求】 1. 什么是核磁共振?什么是脉冲波核磁共振? 2. 发生核磁共振时,横向磁化强度矢量 M 如何改变? 3. 90o 和 180o 射频脉冲作用时,原子核的磁化强度矢量各如何改变? 4. 如何根据磁化强度矢量的变化来测量核磁共振信号? 5. 测量弛豫时间 T1 和 T2 各用什么方法? 6. 怎样观测实验样品的核磁共振成像? 【实验原理】 一. 脉冲核磁共振基本原理 1.脉冲改变核磁化强度状态 处于恒定磁场 B0(沿 z 轴方向)中的原子核自旋系统,其宏观磁化强度 M 以角频率 0 B0 = 绕 B0 进动,垂直于 B0 方向上施加一射频脉冲。在射频脉冲作用前,M 处于热平 衡状态,方向与 z 轴重合;施加射频脉冲作用时,射频脉冲诱发两种能态间的原子核产生能 态跃迁,被激励的原子核从低能态跃迁到高能态,出现核磁共振。受到射频脉冲激励的原子 核的磁化强度 M 偏离原来的平衡状态而发生变化,其变化程达的位置度取决于所施加射频 脉冲的强度和时间。施加的射频脉冲越强,持续时间越长,在射频脉冲停止时,M 离开其平 衡状态越远。在核磁共振成像技术中使用较多的是 90°、180°射频脉冲。施加 90°脉冲时,宏 观磁化矢量M以螺旋运动的形式离开其原来的平衡状态,脉冲停止时,M垂直于主磁场B0, 如图 3-2-10 所示。 90°脉冲结束时,宏观磁化矢量 M 平行于 xy 平面,纵向磁化矢量 Mz=0,横向磁化矢 量 Mxy 最大,如图 3-2-11 所示。这时质子群几乎以同样的相位旋进。施加 180°脉冲后,M 与 B0 平行,但方向相反,横向磁化矢量 Mxy为零,如图 3-2-12 所示。 2.核磁化强度的弛豫过程 脉冲停止后,M 仍围绕 B0 轴旋转,M 末端螺旋上升逐渐靠向 B0,这个过程称之为“核 磁弛豫”。以 90o 脉冲来说明射频脉冲停止后 M 的弛豫变化。如图 3-2-13 所示,在脉冲结束 的一瞬间,M 在 xy 平面上分量 Mxy达最大值,在 z 轴上分量 Mz 为零。当恢复到平衡时,纵 向分量 Mz 重新出现,而横向分量 Mxy消失。在弛豫过程中磁化矢量 M 强度并不恒定,故这 两个弛豫过程的特征分别用纵向弛豫时间(longitudinal relaxation time)T1 和横向弛豫时间 (transverse relaxation time)T2 来描述
,冲后的 图3-21090°射频脉冲作用的质子磁矩进动路径及到达位置 图3-2-1190°脉冲后横向磁化矢量M,达到最大 图3-2-12180°脉冲后横向磁化矢量 Mm为0
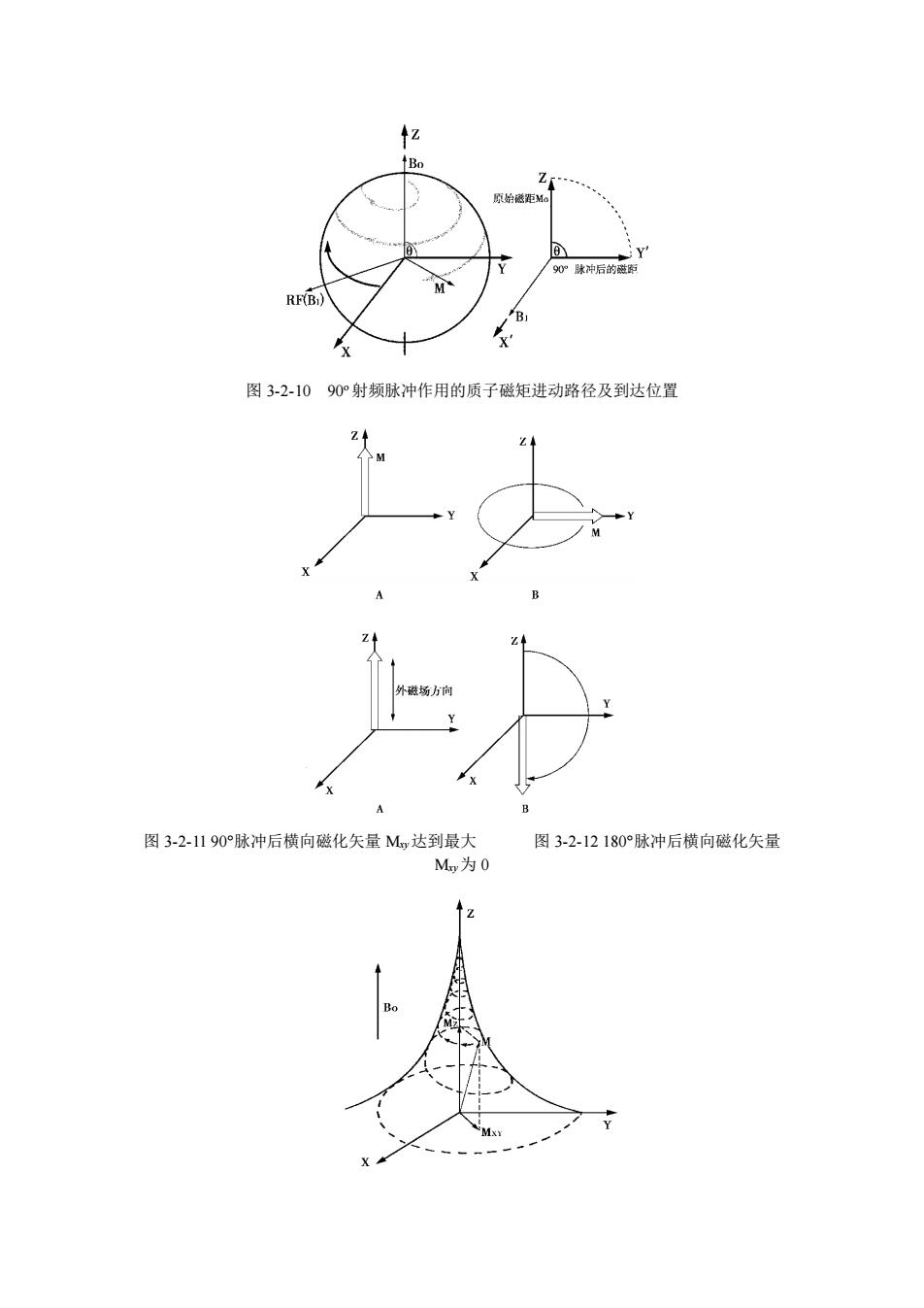
图 3-2-10 90o 射频脉冲作用的质子磁矩进动路径及到达位置 图 3-2-11 90°脉冲后横向磁化矢量 Mxy达到最大 图 3-2-12 180°脉冲后横向磁化矢量 Mxy为 0

图3-2-1390脉冲停止后宏观磁化矢量的变化 (1)纵向驰豫时间 90射频脉冲停止 纵向磁化矢量要逐渐恢复到平衡状态。弛豫过程表现为一种指数 曲线,刀值规定为M达到最终平衡状态63%的时间,如图3-2-14所示。 从微观角度进一步分析纵向弛豫的物理意义。纵向弛豫的快慢主要取决于自旋的原了 核与周围分子(固体中的晶格,液体中的同类分子或溶剂分子)之间的相互作用情况,所以 纵向弛豫(on)又称为自旋.晶格范豫(pir attice re xation)。这种豫 的实质:自旋原子核通过与周围品格的作用传递给周围物质,实现自身能量释放,而从高能 级返回低能级。对于纯液体(譬如水),氢原子核难于丢失自身的能量,因为小的水分子运 动很快。处于高能级状态的氢原子核不能把它们的能量迅速传递给周围晶格,只能慢慢地回 到原来的低能级水平,这意味着液体(譬如水)有较长的。当品格由中等大小的分子构 成,这些分子运动、磁场波动接近于讲动氢原子核的拉草尔频率,则能量传递要有效得名」 很短,比如脂肪酸末端的碳键接近于拉莫尔率,能量传递有效,故脂肪组织具有较短的 时间 图3-214纵向弛豫时间万 (2)横向弛豫时间 90°脉冲的一个作用是激励原子核群使之在同一方位,同步旋进(相位一致),这时横 向磁化矢量M值最大,但射频冲停止后,原子核同步旋进根快变为异步,旋转方位也由 同而异,相位由聚合一致变为丧失聚合而各异(也称为散相),磁化矢量相互抵消,M,很快 由大变小,最后趋向于零。横向磁化矢量衰减也表现为一种指数曲线,T2值规定为横向磁化 矢量衰减到其原来值37%所用的时间,如图3-2-15所示。 Mxr 0.37 横向弛豫 时间 图3-2-15横向驰豫时间2 横向磁化矢量由大变小直至消失的原因:物质分子的热运动持续产生磁场的小波动, 使原子核群由相位一致变为互异,使原子核群进动相位的一致性逐渐散相,横向弛豫 ()也称为自旋-自旋豫(spin-in)。分子结构越均匀,散相
图 3-2-13 90o 脉冲停止后宏观磁化矢量的变化 (1)纵向弛豫时间 90o 射频脉冲停止后,纵向磁化矢量要逐渐恢复到平衡状态。弛豫过程表现为一种指数 曲线,T1 值规定为 Mz达到最终平衡状态 63%的时间,如图 3-2-14 所示。 从微观角度进一步分析纵向弛豫的物理意义。纵向弛豫的快慢主要取决于自旋的原子 核与周围分子(固体中的晶格,液体中的同类分子或溶剂分子)之间的相互作用情况,所以 纵向弛豫(longitudinal relaxation)又称为自旋-晶格弛豫(spin–lattice relaxation)。这种弛豫 的实质:自旋原子核通过与周围晶格的作用传递给周围物质,实现自身能量释放,而从高能 级返回低能级。对于纯液体(譬如水),氢原子核难于丢失自身的能量,因为小的水分子运 动很快。处于高能级状态的氢原子核不能把它们的能量迅速传递给周围晶格,只能慢慢地回 到原来的低能级水平,这意味着液体(譬如水)有较长的 T1。当晶格由中等大小的分子构 成,这些分子运动、磁场波动接近于进动氢原子核的拉莫尔频率,则能量传递要有效得多, T1 很短,比如脂肪酸末端的碳键接近于拉莫尔频率,能量传递有效,故脂肪组织具有较短的 T1。 (2)横向弛豫时间 90°脉冲的一个作用是激励原子核群使之在同一方位,同步旋进(相位一致),这时横 向磁化矢量 Mxy值最大,但射频脉冲停止后,原子核同步旋进很快变为异步,旋转方位也由 同而异,相位由聚合一致变为丧失聚合而各异(也称为散相),磁化矢量相互抵消,Mxy很快 由大变小,最后趋向于零。横向磁化矢量衰减也表现为一种指数曲线,T2 值规定为横向磁化 矢量衰减到其原来值 37%所用的时间,如图 3-2-15 所示。 图 3-2-15 横向弛豫时间 T2 横向磁化矢量由大变小直至消失的原因:物质分子的热运动持续产生磁场的小波动, 使原子核群由相位一致变为互异,使原子核群进动相位的一致性逐渐散相,横向弛豫 (transverse relaxation)也称为自旋-自旋弛豫(spin–spin relaxation)。分子结构越均匀,散相 图 3-2-14 纵向弛豫时间 T1

效果越差,横向磁化减小的越慢,需要的横向弛豫时间了就越长:分子结构越不均匀,散 相效果越好,横向磁化减小越快,乃就越短。另外,乃时间也与所处的磁场均匀性有关,射 频脉冲刚结束时,所有原子核群都以相同相位进动:射 如果不同位置的原子核所 处的磁场强度不一致,其进动频率就发生改变,其进动相位自然也就变得不一致了,T也就 越短。 3.自由感应衰减信号 脉冲核磁共振信号是通过测定横向磁化矢量M的变化得到的 ,从图3-213可知 向磁化矢量垂直并国绕主磁场B旋进,按法拉第定律,矢量M,的变化使环绕在 子核周围的接收线圈(射颊线圈)产生感生电动势,因而产生感生电流,通过放大后即形成 核磁共振信号。90脉冲后,由于受T、T2的影响,磁共振信号以指数曲线形式振荡衰减, 称为自由感应衰减(free induction decay,FID)信号,如图 3-2-16。 二.核磁共振成像基本原理 自由感应衰减 1.核磁共振信号的空间编码 时向 前面所讨论的是处在均匀恒定磁场B中的样品,在射 频脉冲的作用下产生核磁共振,此时接收到的信号来自整个 样品,并没有把它们按空间分布区分开来,无法用来成像。 为了实现核磁共振成像(nuclear magnetic resonance 图3-216自由感应衰减FD信号 imaging,NMRI),必须把收集到的信号进行空间定位。 如前面所述,在均匀的强磁场中,样品内原子核群旋进频率是一致的,如果在主磁场中 再附加一个线性梯度磁场,由于被检样品各部位原子核的旋进频率会因磁场的不同而有所区 别,这样就可对被检样品的某 部位行核磁共振成像,实现对样品的空间定位。梯度破场有 3种:选层梯度场B、频率编码梯度场B、相位编码梯度场B,。这些梯度场的产生是通 3对(x、V、:)梯度线圈产生的,X,V方向的梯度场B、和B,沿垂直于Bo方向,:方向的梯 度场B沿磁场方向。 选层梯度场是在主磁场B。上再附加一个梯度磁场B,(磁感应强度为BG.),则总的 磁感应强度为B+:G,即沿:轴方向自左到右磁感应强度不同,根据核磁共振条件=B0 在样品中沿:轴,不同位置就有不同的共振角频率 m.=y(B+G)=4+△@ (3-2-25) 根据不同频率进行检测,则在垂直于:轴方向上样品就被分割成一个个横向断面,以90°脉 冲激励,则测量结果就为样品被选层的核磁共振信 如图32-17所示 度场B,选出横向层面后,在垂直于:轴的y方狗上分别 梯度场Bx(Bx=xGz)和相位编码梯度场B(B)Gz),这样就能在空间定义某一体积元AVr, 这一体积元中的物体的共振角频率等于 @p=Y(Bo+G,x+G,y+G.=) (3-2-26) 这就是梯度场对自旋体系的空间编码。 2.傅里叶变换成像方法
效果越差,横向磁化减小的越慢,需要的横向弛豫时间 T2 就越长;分子结构越不均匀,散 相效果越好,横向磁化减小越快,T2 就越短。另外,T2 时间也与所处的磁场均匀性有关,射 频脉冲刚结束时,所有原子核群都以相同相位进动;射频结束后,如果不同位置的原子核所 处的磁场强度不一致,其进动频率就发生改变,其进动相位自然也就变得不一致了,T2 也就 越短。 3.自由感应衰减信号 脉冲核磁共振信号是通过测定横向磁化矢量 Mxy 的变化得到的。从图 3-2-13 可知,横 向磁化矢量 Mxy 垂直并围绕主磁场 B0 旋进,按法拉第定律,磁矢量 Mxy 的变化使环绕在原 子核周围的接收线圈(射频线圈)产生感生电动势,因而产生感生电流,通过放大后即形成 核磁共振信号。90°脉冲后,由于受 T1、T2 的影响,磁共振信号以指数曲线形式振荡衰减, 称为自由感应衰减(free induction decay,FID)信号,如图 3-2-16。 二. 核磁共振成像基本原理 1. 核磁共振信号的空间编码 前面所讨论的是处在均匀恒定磁场 B0 中的样品,在射 频脉冲的作用下产生核磁共振,此时接收到的信号来自整个 样品,并没有把它们按空间分布区分开来,无法用来成像。 为了实现核磁共振成像 ( nuclear magnetic resonance imaging ,NMRI),必须把收集到的信号进行空间定位。 如前面所述,在均匀的强磁场中,样品内原子核群旋进频率是一致的,如果在主磁场中 再附加一个线性梯度磁场,由于被检样品各部位原子核的旋进频率会因磁场的不同而有所区 别,这样就可对被检样品的某一部位行核磁共振成像,实现对样品的空间定位。梯度磁场有 3 种:选层梯度场 Bz、频率编码梯度场 Bx、相位编码梯度场 By。这些梯度场的产生是通过 3 对(x、y、z)梯度线圈产生的,x,y 方向的梯度场 Bx 和 By 沿垂直于 B0 方向,z 方向的梯 度场 Bz沿磁场方向。 选层梯度场是在主磁场 B0 上再附加一个梯度磁场 Bz(磁感应强度为 Bz=zGz),则总的 磁感应强度为 B0+zGz,即沿 z 轴方向自左到右磁感应强度不同,根据核磁共振条件 ω0=γB0, 在样品中沿 z 轴,不同位置就有不同的共振角频率 z = + = + (B zG 0 z 0 z ) (3-2-25) 根据不同频率进行检测,则在垂直于 z 轴方向上样品就被分割成一个个横向断面,以 90°脉 冲激励,则测量结果就为样品被选层的核磁共振信号,如图 3-2-17 所示。 在启动选层梯度场 Bz选出横向层面后,在垂直于 z 轴的 x,y 方向上分别启动频率编码 梯度场 Bx(Bx=xGz)和相位编码梯度场 By(By=yGz),这样就能在空间定义某一体积元Vxyz, 这一体积元中的物体的共振角频率等于 0 ( ) xyz x y z = + + + B G x G y G z (3-2-26) 这就是梯度场对自旋体系的空间编码。 2. 傅里叶变换成像方法 图 3-2-16 自由感应衰减 FID 信号

在三个相互垂直的梯度磁场的作用下,体积元△V所产生的自由感应衰成D信号 △S在以角率0旋转的坐标系中等于 AS()=Mop(x.y.=)-AV-exp-ir[[G,()x+G,().y+G.()-=ld (3.2.27) 式中M为体系的磁化矢量,px,,)为核密度空间分布。全部物体的FD信号S是上 式对体积元的三重积分,即 S(t)=[[[Mo-P(x.y.=)-exp-iy[[G,(t)x+G,(t)-y+G.(t)-=]dt'ldxdyd (3-2-28) 可见S()与(x,y)互为傅里叶变换对,对S(T)做反傅里叶变换,即可求得核密度空间 分布,当以图形的形式表示核密度空间分布P(x,八,)时,就得到物体的核磁共振成像, 如图3-2-18所示。 选层榜度 步像 访洗层 B 一一相位重聚梯度 始数锅 重聚无 图3-2-17选层梯度场和选层原理 图3-2-18核磁共振影像的形成 三.核磁共振图像重建的脉冲序列 核磁共振的脉冲序列是为了获取足觞用以重律图像的信号按照一定时序和周期重复施 加的射频脉冲和梯度脉冲的组合。根据重建图像所用信号的来源不同,脉冲序列分为 大类 直接采用FID信号重建图像的序列(硬脉冲FID序列)、采用自旋回波信号重建图像的序列 以及采用梯度回波信号重建图像的序列。 1.硬脉冲自由感应衰减D序列和共振须率测量 硬冲FD序别加网3.2.1g所元 这种脉冲的强度大,作用时间短,利用傅里叶变换 (时间域和频率域之 的变换)后可知这种脉冲对应的频率范围宽,因而能够 把射频线圈 用范围内的不同位置原子核(在不同位置时,由于恒定磁场的不均匀性不同位置处的原子核 的磁场略有不同)激发发生核磁共振。 每一个90°射频脉冲后,原子核的酸矩将产生一个最大的宏观横向磁化矢量4,90脉
在三个相互垂直的梯度磁场的作用下,体积元Vxyz 所产生的自由感应衰减 FID 信号 S 在以角频率 ω0 旋转的坐标系中等于 ( ) ( , , ) exp [ ( ') ( ') ( ') ] ' 0 0 t xyz x y z = − + + S t M x y z V i G t x G t y G t z dt (3-2-27) 式中 M0 为体系的磁化矢量, ( , , ) x y z 为核密度空间分布。全部物体的 FID 信号 S(T)是上 式对体积元的三重积分,即 ( ) ( , , ) exp [ ( ') ( ') ( ') ] ' 0 0 t x y z S t M x y z i G t x G t y G t z dt dxdydz = − + + (3-2-28) 可见 S(T)与 ( , , ) x y z 互为傅里叶变换对,对 S(T)做反傅里叶变换,即可求得核密度空间 分布,当以图形的形式表示核密度空间分布 ( , , ) x y z 时,就得到物体的核磁共振成像, 如图 3-2-18 所示。 三. 核磁共振图像重建的脉冲序列 核磁共振的脉冲序列是为了获取足够用以重建图像的信号按照一定时序和周期重复施 加的射频脉冲和梯度脉冲的组合。根据重建图像所用信号的来源不同,脉冲序列分为三大类: 直接采用 FID 信号重建图像的序列(硬脉冲 FID 序列)、采用自旋回波信号重建图像的序列 以及采用梯度回波信号重建图像的序列。 1. 硬脉冲自由感应衰减 FID 序列和共振频率测量 硬脉冲 FID 序列如图 3-2-19 所示,这种脉冲的强度大,作用时间短,利用傅里叶变换 (时间域和频率域之间的变换)后可知这种脉冲对应的频率范围宽,因而能够把射频线圈作 用范围内的不同位置原子核(在不同位置时,由于恒定磁场的不均匀性不同位置处的原子核 的磁场略有不同)激发发生核磁共振。 每一个 90°射频脉冲后,原子核的磁矩将产生一个最大的宏观横向磁化矢量 Mxy ,90°脉 图 3-2-17 选层梯度场和选层原理 图 3-2-18 核磁共振影像的形成