
SV=常量 流体的连续性方程 SV=Q称为液体的体积流量 结论:不可压缩的流体在流管内作稳定流动 时,流体的流速和管的横截面积成反比。 问题:血液在大动脉中流速大还是在毛细管 中流速大? 大动脉中流速大 28910
结论:不可压缩的流体在流管内作稳定流动 时,流体的流速和管的横截面积成反比。 SV=Q 称为液体的体积流量 问题:血液在大动脉中流速大还是在毛细管 中流速大? 大动脉中流速大 s v = 常量 流体的连续性方程
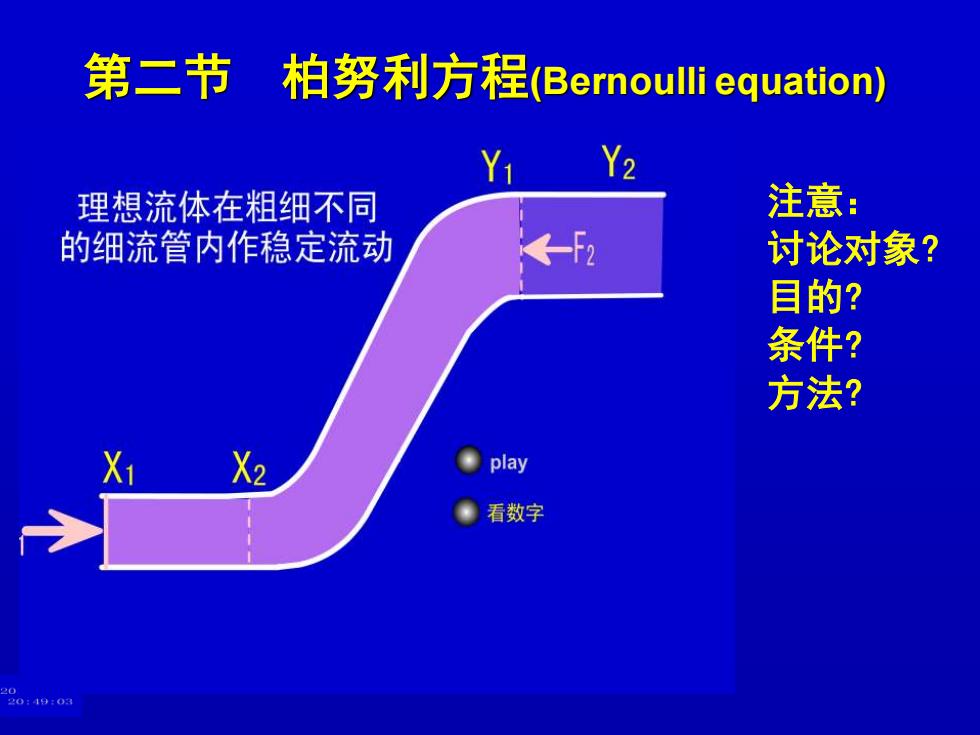
第二节柏努利方程(Bernoulli equation) Y1 Y2 理想流体在粗细不同 注意: 的细流管内作稳定流动 ← 讨论对象? 目的? 条件? 方法? X2 ●play 。看数字 2 2049:0
第二节 柏努利方程(Bernoulli equation) 注意: 讨论对象? 目的? 条件? 方法?

推导: ①外力作功:W=FL1F2L2 P1S1L1-P2S2L2 理想流体时: SL1=S2L2=V(体积) .W=(p1-P2)V ②机械能的改变量: △E=E2一E m2gh2+m2V22/2-m1gh1-m1V12/2 e88909
推导: ①外力作功:W=F1L1 - F2L2 = p1 s1L1 -p2 s2L2 理想流体时: s1L1= s2L2 =V (体积) ∴ W=( p1 -p2)V ②机械能的改变量: △E =E2-E1 = m2gh2 + m2v2 2/2 - m1gh1 - m1v1 2/2

③不考虑内摩擦,由功能守恒知: Pi-p2)V ( =m2gh2 m2v22/2 migh1 miV 2/2 由于流体不可压缩 ∴.有:mW=m2N=p p1-p2 =p2gh2+P2v22/2-p1gh1-p122 由此得: B+p+20y=B*p跳+py
③不考虑内摩擦,由功能守恒知: ( p1 -p2)V =m2gh2 + m2v2 2 /2 - m1gh1 - m1v1 2 /2 由于流体不可压缩 ∴有: m1 /V = m2 /V = ρ 由此得: p1 -p2 =ρ2gh2 + ρ2v 2 2 /2 - ρ1gh1 - ρ1v1 2 /2

即:P+pgh+pV2=恒量 2 此即伯努利方程 它表明了流体中单位体积内的动能和重力势能以及 该点的压强之和为一常数。 柏努利方程说明了压强、高度、流速间的关系。 问题:三者为什么可以相加?三者相加的物理意义 是什么?单位统一吗? pv/2称为动压强,P、pgh称为静压强。 应用条件:理想流体作稳定流动 返 28910
此即伯努利方程 它表明了流体中单位体积内的动能和重力势能以及 该点的压强之和为一常数。 柏努利方程说明了压强、高度、流速间的关系。 问题:三者为什么可以相加?三者相加的物理意义 是什么?单位统一吗? ρv2/2称为动压强,P、ρgh称为静压强。 应用条件:理想流体作稳定流动 即: 返 回