
拉格朗日乘数(LM) 例子5.3 我们通过对例3.4的犯罪模型略加扩展来说明LM检验: narr86-B+B penv+Bavgsen+B tottime+B ptime86+B qemp86+u 其中,narr86是一个人曾被拘捕的次数,pw是以前被拘捕后被定罪的次数,ags是过去定罪后被判刑 的平均时间长度,tottime是在1986年以前,此人年满18岁后被送进监狱的总时间,ptime86是1986年坐牢 的月数,而gmp86是此人在1986年合法就业的季度数。我们要使用LM统计量检验的原假设是:在控制了 其他因素后,avgsen和tottime对arr86没有影响。 在第(i)步,我们通过将arr86对p、ptime86和qemp86进行回归来估计约束模型;回归中排除了 变量agse1和toltime。我们从这个回归中得到2725个残差a。接下来,我们将 a对pcnu、ptimes86、qenp86、avgsen和tottime进行回归 (5.15) 和平常一样,我们列出自变量的顺序是无所谓的。第二个回归产生了R,结果其大小约为0.0015。这可能 看起来很小,但我们必须将它乘以n才能得到LM统计量:LM=2725×0.0015≈4.09。自由度为2的卡方 分布在显著性水平为10%时的临界值是4.61(保留到小数点后两位;参见表G.4)。于是,我们在10%的水 平上不能拒绝原假设Rm=0和Bw=0。因为p值等于P(X>4.09)≈0.129,所以我们在15%的水平上 将拒绝H。 作为比较,对agsm和tottime联合显著性的F检验所得到的p值约等于O.l3l,它与使用LM统计量 所得到的p值相当接近。这无足为奇,因为这两个统计量犯第I类错误的概率(渐近地)相同。(即在原假 设正确时,它们以相同的频率拒绝原假设。)】 6 中级计量经济学
拉格朗日乘数(LM) 例子5.3 6 中级计量经济学

拉格朗日乘数(LM)-拓展 要找函数z=f(x,y)在条件p(x,y)=0下的 可能极值点, 1.先构造函数F(x,y)=f(x,y)+九p(x,y), 其中入为拉格朗日乘数. 2.由 fx(x,y)+九p(x,y)=0, f,(x,y)+九p(x,y)=0, p(x,y)=0. 解出x,y,2,其中(x,y)就是可能的极值点的坐 标. 中级计量经济学
要找函数z = f (x, y)在条件(x, y) = 0下的 可能极值点, 1. 先构造函数F(x, y) = f (x, y) + (x, y), 其中 为拉格朗日乘数. 2. 由 = + = ( , ) 0. ( , ) ( , ) 0, ( , ) ( , ) 0, x y f x y x y f x y x y y y x x 解出x, y,,其中( x, y)就是可能的极值点的坐 标. 拉格朗日乘数(LM)-拓展 7 中级计量经济学

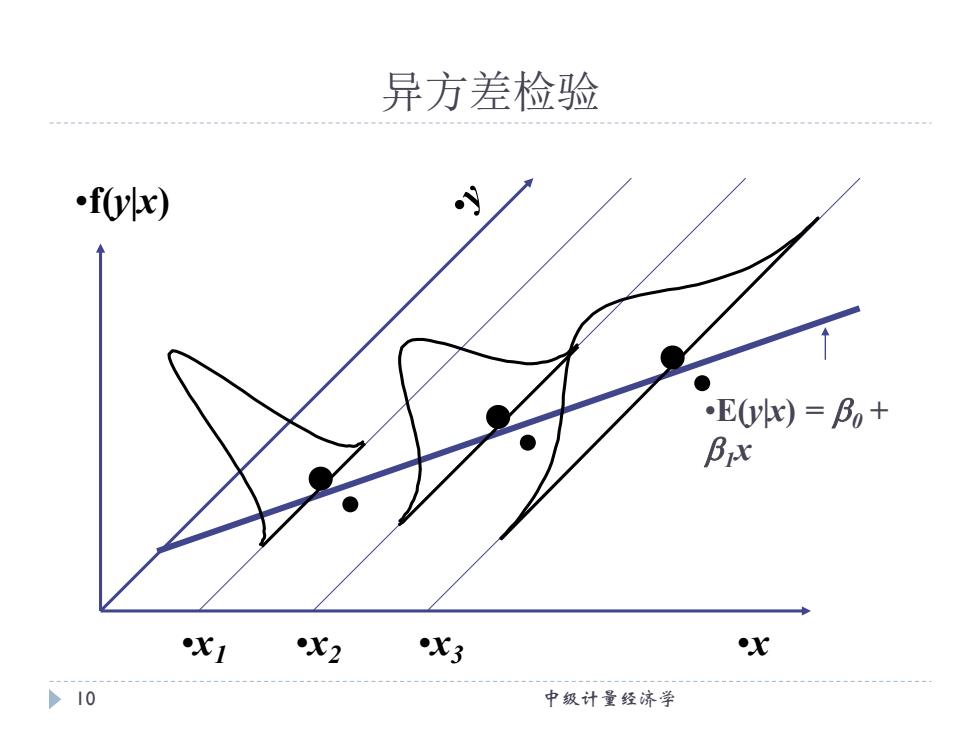
异方差检验 一、什么是异方差 设一元回归模型为: y=Bo+Bx;+8 其中, var(s)=E(s,-E())=E(s) 异方差性可表示为:Y,的条件方差随解释变量X 取值的变化而变化。即: E(62)=o1 >8 中级计量经济学
设一元回归模型为: i i i y = + x + 0 1 其中, ( ) ( ( )) ( ) 2 2 var i E i E i E i = − = 异方差性可表示为: Yi 的条件方差随解释变量 Xi 取值的变化而变化。即: ( ) 2 2 E i i = 异方差检验 一、什么是异方差 8 中级计量经济学

异方差检验 回顾chp3,异方差性的假定暗含在解释变量条件下无 法观测到的误差U的方差为常数 如果这一假定不能满足,即如果对于X的不同值来说u的 方差是不同的,那么该误差具有异方差性 例子:教育回报率 如果能力是无法观测到的,那么我们认为能力的方 差依据获得教育程度的不同而不同 >9 中级计量经济学
回顾chap3,异方差性的假定暗含在解释变量条件下无 法观测到的误差u的方差为常数 如果这一假定不能满足,即如果对于x的不同值来说u的 方差是不同的, 那么该误差具有异方差性 例子: 教育回报率 如果能力是无法观测到的, 那么我们认为能力的方 差依据获得教育程度的不同而不同 异方差检验 9 中级计量经济学
异方差检验 f(vx) E(Vx)=Bo+ Bix 比1x2x3 x >10 中级计量经济学
异方差检验 • . •x1 •x2 •x •f(y|x) •x3 • . • . •E(y|x) = 0 + 1x 10 中级计量经济学