
声光效应实验 【实验目的】 1,了解声光效应的原理。 2.了解、观察喇曼一纳斯衍射和布喇格衍射的实验条件和特点,加深对其概念的理解 3.测量声光器件Brag衍射效率和喇曼一纳斯衍射效率。 4.测量声光器件中心频率和带宽 5.测量声光偏转角与超声波频率间关系,绘制声光偏转曲线,计算介质中声速。 6.测量Bg熙衍射光光强与超声波驱动功率间关系,绘制声光调制曲线 7.模拟激光通讯实验。 【实验原理】 当超声波在介质中传播时,将引起介质的弹性应变作时间上和空间上的周期性的变化,并且导致介 质的折射率也发生相应的变化。当光束通过有超声波的介质后就会产生衍射现象,这就是声光效应。有 超声波传播若的介质如同一个相位光栅。 19 b 0 k 图1:声光衍射 声光效应有正常声光效应和反常声光效应之分。在各向同性介质中,声-光相互作用不导致入射光 偏振状态的变化,产生正常声光效应。在各向异性介质中,声一光相互作用可能导致入射光偏振状态的 变化,产生反常声光效应。反常声光效应是制造高性能声光偏转器和可调滤光器的物理基础。正常声光 效应可用喇曼-纳斯的光栅假设作出解释,而反常声光效应不能用光栅假设作出说明。在非线性光学
声光效应实验 声光效应实验 【实验目的】 1. 了解声光效应的原理。 2. 了解、观察喇曼—纳斯衍射和布喇格衍射的实验条件和特点, 加深对其概念的理解。 3. 测量声光器件 Bragg 衍射效率和喇曼—纳斯衍射效率。 4. 测量声光器件中心频率和带宽 5. 测量声光偏转角与超声波频率间关系,绘制声光偏转曲线,计算介质中声速。 6. 测量 Bragg 衍射光光强与超声波驱动功率间关系,绘制声光调制曲线 7. 模拟激光通讯实验。 【实验原理】 当超声波在介质中传播时,将引起介质的弹性应变作时间上和空间上的周期性的变化,并且导致介 质的折射率也发生相应的变化。当光束通过有超声波的介质后就会产生衍射现象,这就是声光效应。有 超声波传播着的介质如同一个相位光栅。 声光效应有正常声光效应和反常声光效应之分。在各向同性介质中,声-光相互作用不导致入射光 偏振状态的变化,产生正常声光效应。在各向异性介质中,声-光相互作用可能导致入射光偏振状态的 变化,产生反常声光效应。反常声光效应是制造高性能声光偏转器和可调滤光器的物理基础。正常声光 效应可用喇曼-纳斯的光栅假设作出解释,而反常声光效应不能用光栅假设作出说明。在非线性光学 ks b 2 b 2 L 2 χ y k 0 L 2 θ 图 1:声光衍射 1

中,利用参量相互作用理论,可建立起声一光相互作用的统一理论,并且运用动量匹配和失配等概念对 正常和反常声光效应都可作出解释。本实验只涉及到各向同性介质中的正常声光效应。 设声光介质中的超声行波是沿y方向传播的平面纵波,其角频率为w,波长为,波矢为k。1射 光为沿x方向传播的平面波,其角频率为”,在介质中的波长为方,波矢为k。介质内的弹性应变也以行 波形式随声波一起传播。由于光速大约是声波的10倍,在光波通过的时间内介质在空间上的周期变化 可看成是固定的。 由于应变而引起的介质折射率的变化由下式决定 A)-PS (1) 式中,n为介质折射率,S为应变,P为光弹系数。通常,P和S为二阶张量。当声波在各向同性介质中 传播时,P和S可作为标量处理,如前所述,应变也以行波形式传播,所以可写成 S=S.sin(@,t-k,y) (2) 当应变较小时,折射率作为y和1的函数可写作 n(y,t)=n+Ansin(o,t-k,y) (3) 式中,%为无超声波时的介质折射率,△n为声波折射率变化的幅值,由(1)式可求出 An=-n'PSo 设光束垂直入射(kLk)并通过厚度为L的介质,则前后两点的相位差为 △p=k,1)L =△4+6sim(w,-k,y) =knL+k△nLsn",-ky) (4) 式中,为入射光在真空中的波矢的大小,右边第一项△为不存在超声波时光波在介质前后二点的相 位差,第二项为超声波引起的附加相位差(相位调制),动%△L。可见,当平面光波入射在介质的 前界面上时,超声波使出射光波的波阵面变为周期变化的皱折波面,从而改变了出射光的传播特征,使 光产生衍射。 设入射面上x=-LU2的光振动为E=Am,A为一常数,也可以是复数。考虑到在出射面x=L2上各 点相位的改变和调制,在平面内离出射面很远一点处的衍射光叠加结果为 E-d 写成一等式时, ECed (5) 式中,b为光束宽度,0为衍射角,C为与A有关的常数,为了简单可取为实数。利用一与贝塞耳函数有 关的恒等式
声光效应实验 中,利用参量相互作用理论,可建立起声-光相互作用的统一理论,并且运用动量匹配和失配等概念对 正常和反常声光效应都可作出解释。本实验只涉及到各向同性介质中的正常声光效应。 设声光介质中的超声行波是沿 у 方向传播的平面纵波,其角频率为 ws,波长为 λs,波矢为 ks。λ 射 光为沿 х 方向传播的平面波,其角频率为 w,在介质中的波长为 λ,波矢为 k。介质内的弹性应变也以行 波形式随声波一起传播。由于光速大约是声波的 105 倍,在光波通过的时间内介质在空间上的周期变化 可看成是固定的。 由于应变而引起的介质折射率的变化由下式决定 ) 1 ( 2 n ∆ =PS (1) 式中,n 为介质折射率,S 为应变,P 为光弹系数。通常,P 和 S 为二阶张量。当声波在各向同性介质中 传播时,P 和 S 可作为标量处理,如前所述,应变也以行波形式传播,所以可写成 sin( ) 0 S S t k y = ωs − s (2) 当应变较小时,折射率作为 y 和 t 的函数可写作 ( , ) sin( ) 0 n y t n n t k y = + ∆ ωs − s (3) 式中,n0为无超声波时的介质折射率,△n 为声波折射率变化的幅值,由(1)式可求出 0 3 2 1 ∆n = − n PS 设光束垂直入射(k⊥ks)并通过厚度为 L 的介质,则前后两点的相位差为 ∆φ = k0n( y,t)L sin( ) 0 w k y = ∆φ +δφ s − s sin( ) 0 0 k nL k nL w k y = + ∆ s − s (4) 式中,k0 为入射光在真空中的波矢的大小,右边第一项△ф0 为不存在超声波时光波在介质前后二点的相 位差,第二项为超声波引起的附加相位差(相位调制),δф= k0△nL 。可见,当平面光波入射在介质的 前界面上时,超声波使出射光波的波阵面变为周期变化的皱折波面,从而改变了出射光的传播特征,使 光产生衍射。 设入射面上 x=-L/2 的光振动为 Ei =Aeiwt,A 为一常数,也可以是复数。考虑到在出射面 x=L/2 上各 点相位的改变和调制,在 xy 平面内离出射面很远一点处的衍射光叠加结果为 [ ] ∫− − − ∝ / 2 / 2 0 ( , ) 0 sin b b i t k n y t L k y E A e dy ω θ 写成一等式时, ∫− − − = / 2 / 2 sin( ) sin 0 b b i t i k y t ik y E Ce e e dy ω dφ S ωS θ (5) 式中,b 为光束宽度,θ 为衍射角,C 为与 A 有关的常数,为了简单可取为实数。利用一与贝塞耳函数有 关的恒等式 2

em0-∑J(ae0 式中J(a)为(第一类)m阶贝塞耳函数,将(5)式展开并积分得 E=Cb)e sin[b(mk,k sin)/2] (6) b(mk,-k。sin0)/2 上式中与第m级衍射有关的项为 E=Ee"o-me) (7) E=Ch)sinb(mkk sin0)/2] (8) b(mk,-ko sine)/2 因为函数sinx/x在x=0时取极大值,因此衍射极大的方位角日n由下式决定 m0,=mi+m经 (9) 式中,为真空中光的波长,s为介质中超声波的波长。与一般的光栅方程相比可知,超声波引起的有 应变的介质相当于一光橱常数为超声波长的光橱。由(7)式可知,第m级衍射光的频率wm为 0n=0-m0, (10) 可见,衍射光仍然是单色光,但发生了频移。由于w>,这种频移是很小的。 第m级衍射极大的强度1m可用(7)式模数平方表示: 1n=EE6=C2b2J(6) (11) 式中,E为E的共轭复数,0C。 第m级衍射极大的衍射效率m定义为第m级衍射光的强度与入射光强度之比。由(I1)式可知, ”m正比于子m(动)。当m为整数时,Jm(a)=()(a。由(9)式和(11)式表明,各级射光相对于零 级对称分布。 当光束斜入射时,如果声光作用的距离满足L<2./,则各级衍射极大的方位角0由下式决定 sm0,=咖1+m2 (12) 式中1为入射光波矢k与超声波波面之间的夹角。上述的超声衍射称为喇曼纳斯衍射,有超声波存在的 介质起一平面相位光栅的作用
声光效应实验 ∑ ∞ =−∞ = m im m ia e J a e θ θ ( ) sin 式中 Jm(α)为(第一类)m 阶贝塞耳函数,将(5)式展开并积分得 ∑ ∞ =−∞ − − − = m s i m t s m b mk k b mk k E Cb J e s ( sin )/ 2 sin[ ( sin )/ 2] ( ) 0 ( ) 0 θ θ δφ ω ω (6) 上式中与第 m 级衍射有关的项为 ( ) 0 i m t m s E E e ω− ω = (7) ( sin )/ 2 sin[ ( sin )/ 2] ( ) 0 0 0 θ θ δφ b mk k b mk k E CbJ s s m − − = (8) 因为函数sin x x 在 x = 0 时取极大值,因此衍射极大的方位角θ m 由下式决定 s m i m λ λ θ 0 sin = sin + (9) 式中,λ0 为真空中光的波长,λS 为介质中超声波的波长。与一般的光栅方程相比可知,超声波引起的有 应变的介质相当于一光栅常数为超声波长的光栅。由(7)式可知,第 m 级衍射光的频率 wm为 ω m =ω − mωs (10) 可见,衍射光仍然是单色光,但发生了频移。由于 w>>ws ,这种频移是很小的。 第 m 级衍射极大的强度 Im可用(7)式模数平方表示: ( ) * 2 2 2 Im = E0E0 = C b Jm δφ (11) 式中,E*0为 E0的共轭复数,I0=C2 b2 。 第 m 级衍射极大的衍射效率 ηm定义为第 m 级衍射光的强度与入射光强度之比。由(11)式可知, ηm正比于 J 2 m(δф)。当m为整数时,J- m(α)=(-1)m Jm(α)。由(9)式和(11)式表明,各级衍射光相对于零 级对称分布。 当光束斜入射时,如果声光作用的距离满足 L<2λS 2 /λ,则各级衍射极大的方位角 θm由下式决定 s m i m λ λ θ 0 sin = sin + (12) 式中 i 为入射光波矢 k 与超声波波面之间的夹角。上述的超声衍射称为喇曼-纳斯衍射,有超声波存在的 介质起一平面相位光栅的作用。 3

图2:布喇格衍射 当声光作用的距离满足L>2/,而且光束相对于超声波波面以某一角度斜入射时,在理想情况 下除了0级之外,只出现1级或者1级衍射。如图2所示。这种衍射与晶体对X光的布喇格衍射很类 似,故称为布喇格衍射。能产生这种衍射的光束入射角称为布喇格角。此时的有超声波存在的介质起体 积光栅的作用。可以证明,布喇格角满足 sinin=2元, (13) 式中(13)称为布喇格条件。因为布喇格角一般都很小,故衍射光相对于入射光的偏转角中为 =2。*= 元n (14) 式中,为超声波波速,人为超声波频率,其它量的意义同前。在布喇格衍射的情况下,一级衍射光的 衍射效率为 =m经开) (15) 式中,Ps为超声波功率,L和H为超声换能器的长和宽,M为反映声光介质本身性质的一常数, M2=np2(Pv,),p为介质密度,P为光弹系数。在布喇格衍射下,衍射光的频率也由(10)式决 定。 理论上布喇格衍射的衍射效率可达到100%,喇曼-纳斯衍射中一级衍射光的最大衍射效率仅为 34%,所以实用的声光器件一般都采用布喇格衍射。 由(14)式和(15)式可看出,通过改变超声波的频率和功率,可分别实现对激光束方向的控制和 强度的调制,这是声光偏转器和声光调制器的物理基础。从(10)式可知,超声光栅衍射会产生频移, 因此利用声光效应还可制成频移器件。超声频移器在计量方面有重要应用,如用于激光多普勒测速仪 4
声光效应实验 当声光作用的距离满足 L>2λS 2 /λ,而且光束相对于超声波波面以某一角度斜入射时,在理想情况 下除了 0 级之外,只出现 1 级或者-1 级衍射。如图 2 所示。这种衍射与晶体对 X 光的布喇格衍射很类 似,故称为布喇格衍射。能产生这种衍射的光束入射角称为布喇格角。此时的有超声波存在的介质起体 积光栅的作用。可以证明,布喇格角满足 s Bi λ λ 2 sin = (13) 式中(13)称为布喇格条件。因为布喇格角一般都很小,故衍射光相对于入射光的偏转角 ф 为 s s s B f n i n λ λ λ f 0 = 2 ≈ = (14) 式中,νS 为超声波波速,fS 为超声波频率,其它量的意义同前。在布喇格衍射的情况下,一级衍射光的 衍射效率为 ) 2 sin ( 2 0 2 H M LPs λ π η = (15) 式中,PS 为超声波功率,L 和 H 为超声换能器的长和宽,M2 为反映声光介质本身性质的一常数, /( ) 6 2 M2 = n p ρn s , ρ 为介质密度,P 为光弹系数。在布喇格衍射下,衍射光的频率也由(10)式决 定。 理论上布喇格衍射的衍射效率可达到 100%,喇曼-纳斯衍射中一级衍射光的最大衍射效率仅为 34%,所以实用的声光器件一般都采用布喇格衍射。 由(14)式和(15)式可看出,通过改变超声波的频率和功率,可分别实现对激光束方向的控制和 强度的调制,这是声光偏转器和声光调制器的物理基础。从(10)式可知,超声光栅衍射会产生频移, 因此利用声光效应还可制成频移器件。超声频移器在计量方面有重要应用,如用于激光多普勒测速仪 等。 图 2:布喇格衍射 4
以上讨论的是超声行波对光被的衍射。实际上,超声驻波对光波的衍射也产生喇品纳斯衍射和布制 格衍射,而且各衍射光的方位角和超声频率的关系与超声行波时的相同。不过,各级衍射光不再是简单 地产生频移的单色光,而是含有多个傅里叶分量的复合光。 【实验仪器】 一套完整的声光实验仪配有:声光器件、半导体激光器、功率信号源、光强分布测量仪及光具座 每个器件都带有l0的立杆,可以安插在通用光具座上,如图3所示。 示波署 声光功率信号源 光强分布测量仪 转角平台 频率计 激光器 图3:声光效应实验安装图 1.声光器件 声光器件的结构示意图如图4所示。它由声光介质、压电换能器和吸声材料组成 吸声材料 转角平 声光器件 旋转手轮 声光介质 转角平台 光波前进方向 一压电换能器 图4:声光器件的结构 图5:转角平台 本实验采用的声光器件是二氧化锑,在此介质中超声波速度v=4200m/s,吸声材料的作用是吸收 通过介质传播到端面的超声波以建立超声行波。将介质的端面磨成斜面或成牛角状,也可达到吸声的作 用。压电换能器又称超声发生器,由妮酸锂品体或其它压电材料制成。它的作用是将电功率换成声功 率,并在声光介质中建立起超声场。压电换能器既是一个机械振动系统,又是一个与功率信号源相联系 的电振动系统,或者说是功率信号源的负载。为了获得最佳的电声能量转换效率,换能器的阻抗与信号 源内阻应当匹配。声光器件有一个衍射效率最大的工作频率,此频率称为声光器件的中心频率,记为 。对于其它频奉的超声波,其衍射效奉将降低。规定衍射效率(或衍射光的相对光强)下降3b(即 衍射效奉降到最大值的1/√5)时两频率间的间隔为声光器件的带宽
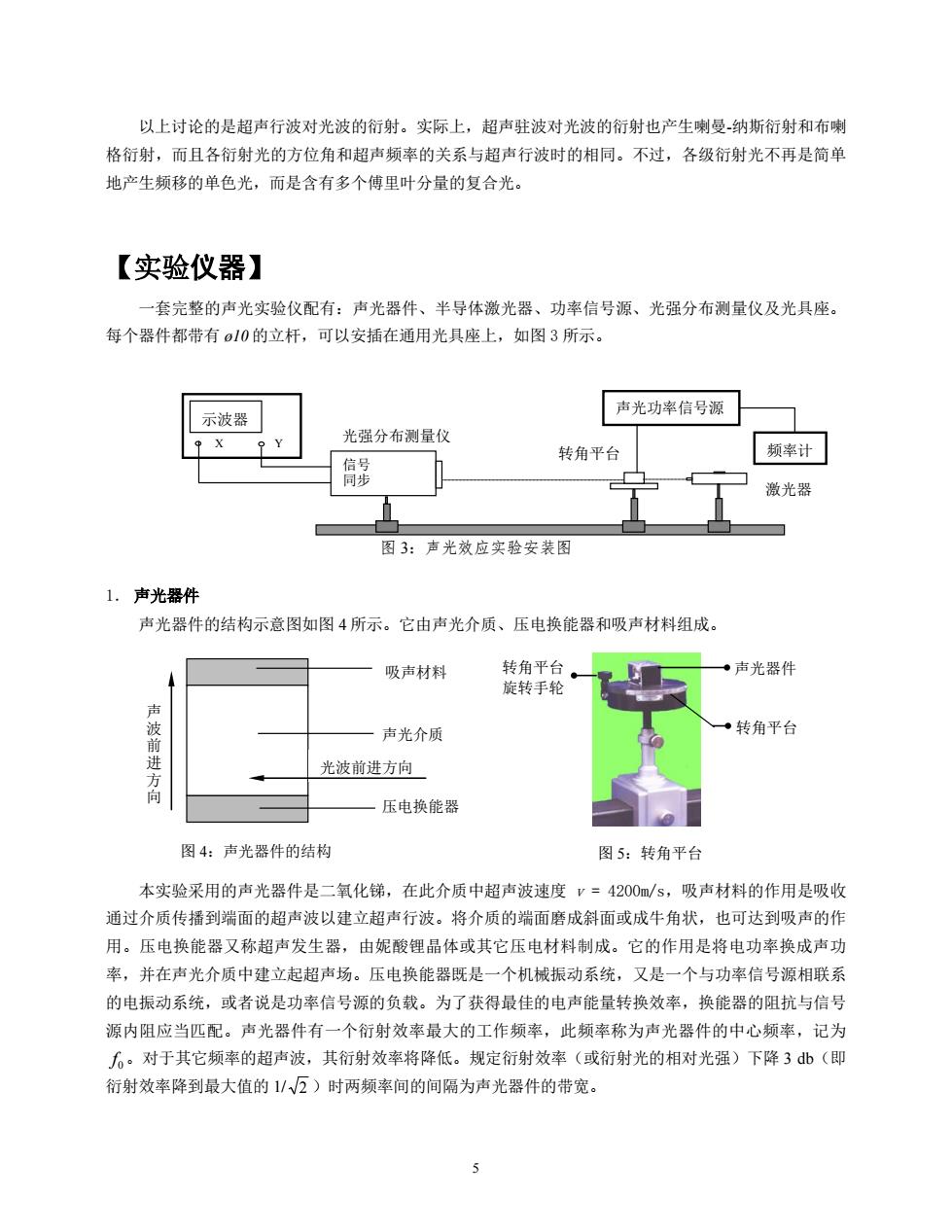
声光效应实验 以上讨论的是超声行波对光波的衍射。实际上,超声驻波对光波的衍射也产生喇曼-纳斯衍射和布喇 格衍射,而且各衍射光的方位角和超声频率的关系与超声行波时的相同。不过,各级衍射光不再是简单 地产生频移的单色光,而是含有多个傅里叶分量的复合光。 【实验仪器】 一套完整的声光实验仪配有:声光器件、半导体激光器、功率信号源、光强分布测量仪及光具座。 每个器件都带有 ø10 的立杆,可以安插在通用光具座上,如图 3 所示。 图 3:声光效应实验安装图 1. 声光器件 声光器件的结构示意图如图 4 所示。它由声光介质、压电换能器和吸声材料组成。 本实验采用的声光器件是二氧化锑,在此介质中超声波速度 v = 4200m/s,吸声材料的作用是吸收 通过介质传播到端面的超声波以建立超声行波。将介质的端面磨成斜面或成牛角状,也可达到吸声的作 用。压电换能器又称超声发生器,由妮酸锂晶体或其它压电材料制成。它的作用是将电功率换成声功 率,并在声光介质中建立起超声场。压电换能器既是一个机械振动系统,又是一个与功率信号源相联系 的电振动系统,或者说是功率信号源的负载。为了获得最佳的电声能量转换效率,换能器的阻抗与信号 源内阻应当匹配。声光器件有一个衍射效率最大的工作频率,此频率称为声光器件的中心频率,记为 0f 。对于其它频率的超声波,其衍射效率将降低。规定衍射效率(或衍射光的相对光强)下降 3 db(即 衍射效率降到最大值的 1/ 2 )时两频率间的间隔为声光器件的带宽。 声光器件 转角平台 转角平台 旋转手轮 图 5:转角平台 吸声材料 声光介质 压电换能器 图 4:声光器件的结构 声 波 前 进 方 向 光波前进方向 信号 同步 声光功率信号源 激光器 转角平台 X Y 光强分布测量仪 示波器 频率计 5