
§7.1无损介质中的均匀平面波 即w=w(z)eP,w→表示E,的任一分量 v-e (. 0=0) Oz Ox 对w≠0的时谐场,仅考虑二个旋度方程即可 V×i=j,+w心 on () 0z 、Vx龙=-jwB x =-jwufi (2)
§ 7.1 无损介质中的均匀平面波 ( ) ( ) jP z 即 ( )z e EH jP z( ) 表示 的任 分量 即 m = , 表示 , 的任一分量 z ˆ , 0) z xy ( ) w 0 对 的时谐场,仅考虑二个旋度方程即可 ˆ (1) f H z jw E H J jwD z ˆ (2) H J jwD f z E jwB E z jw H z jw H (2) z

§7.1无损介质中的均匀平面波 将(2)式代入(1)式可得 2 =k2龙 其中k=wVuE→× =k2元 8z 8z 0z2 a a → 2 0z E=k2E 令龙=龙+龙,(它,=它+它,为横向分量) =0 -0
§ 7.1 无损介质中的均匀平面波 将( )式代入(1)式可得 2 2 2 2 2 ˆ ˆ ˆ ˆ E z z E z z kE k w k E 其中 2 2 2 E E z z z 2 2 2 ˆ ˆ E E z z kE z z ˆ ˆ E E E E Ex Ey z tx t y 令 ( 为横向分量) 2 0 Ez E 2 2 2 0 t t E k E z

§7.1无损介质中的均匀平面波 上式分解成x,y二个分量求解 「E=Enek+Eme 可得店,Ee+Ec 1-TEe 由(2)式可知: me wu k WE
§ 7.1 无损介质中的均匀平面波 把上式分解成 二个分量求解 x y, jkz jkz x xm xm jk jk E Ee Ee 可 得 : 1 1 jkz jkz E y ym ym E e E e 可 得 : 1 1 jkz jkz H y xm xm Ee Ee 由 ( 2 ) 式 可 知 1 1 jkz jkz H x ym ym Ee Ee 由 ( 2 ) 式 可 知 : x ym ym w k w k k w 其中

§7.1无损介质中的均匀平面波 其中的物理概念: e项代表沿+z方向传播的平面波 e项代表沿-z方向传播的平面波 例:它=Eine设Etm=Enem 其中E为实数 则E时(z,t)=E cos(wt-kz+p) 可见随z的增大,E的相位是滞后的,它代表沿+z方向 传播的波。电磁波传播需要一定的时间,沿+z方向传 播时,先达到z,点,后达到z,点,因此2,点的状态总是滞 后于z,点的状态
§ 7.1 无损介质中的均匀平面波 其中的物理概念: jkz jk e z 项代表沿 方向传播的平面波 e z jkz项代表沿- 方向传播的平面波 jkz j 例 设 其中 为实数 ( , ) cos( ) x jkz j x xm xm xm xm x xm x E Ee E Ee E E z t E wt kz 例: 设 其中 为实数 则 ( , ) cos( ) x xm x x t wt k zE z 则 可见随 的增大, 的相位是 的,它代表沿 方向 滞后 1 22 z z zz 传播的波。电磁波传播需要一定的时间,沿 方向传 播时,先达到 1 22 点,后达到 点,因此 点的状态总是滞 1 z zz z 播时,先达到 点,后达到 点,因此 点的状态总是滞 后于 点的状态
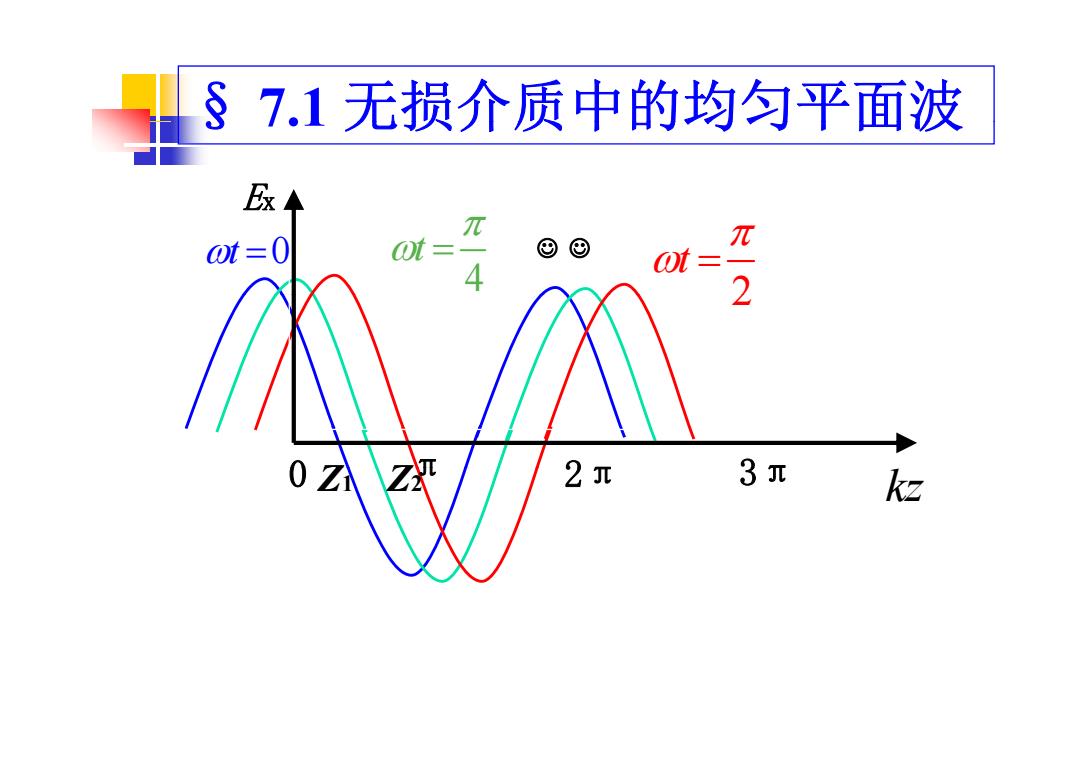
§7.1无损介质中的均匀平面波 E尿本 π ⊙t=0 0t= ©© π 4 wt 2 2 3元 kz
§ 7.1 无损介质中的均匀平面波 Ex t 0 4 t 2 t Ex 2 0 Z Zπ 2π 3π kz 1 Z2